Difference between revisions of "Aufgaben:Exercise 5.5Z: About the Rake Receiver"
m (Text replacement - "RAKE" to "Rake") |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation |
}} | }} | ||
| − | [[File:P_ID1888__Mod_Z_5_5.png|right|frame| | + | [[File:P_ID1888__Mod_Z_5_5.png|right|frame|Two-way channel <br>& rake '''KORREKTUR''': two-way channel, rake receiver]] |
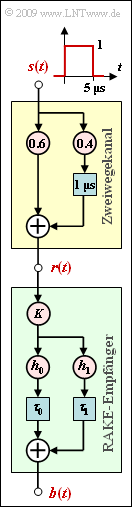
| − | + | The diagram shows a two-way channel (yellow background). The corresponding descriptive equation is: | |
:$$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ | :$$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$ | ||
| − | + | Let the delay on the secondary path be $τ = 1 \ \rm µ s$. Drawn below is the structure of a rake receiver (green background) with general coefficients $K$, $h_0$, $h_1$, $τ_0$ and $τ_1$. | |
| − | + | The purpose of the rake receiver is to combine the energy of the two signal paths, making the decision more reliable. | |
| − | + | The combined impulse response of the channel and the rake receiver can be expressed in the form | |
:$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ | :$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$ | ||
| − | + | but only if the rake coefficients $h_0$, $h_1$, $τ_0$ and $τ_1$ are appropriately chosen. The main part of $h_{\rm KR}(t)$ is supposed to be at $t = τ$. | |
| − | + | The constant $K$ is to be chosen so that the amplitude of the main path $A_1 = 1$ : | |
:$$K= \frac{1}{h_0^2 + h_1^2}.$$ | :$$K= \frac{1}{h_0^2 + h_1^2}.$$ | ||
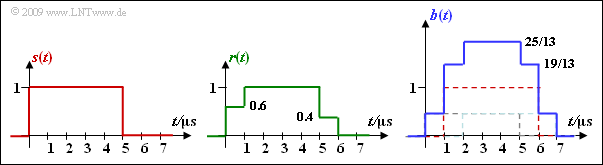
| − | + | Apart from the rake parameters, the signals $r(t)$ and $b(t)$ are sought when $s(t)$ is a rectangle of height $s_0 = 1$ and width $T = \ \rm 5 µ s$. | |
| Line 25: | Line 25: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation|Error Probability of Direct-Sequence Spread Spectrum Modulation]]. |
| − | * | + | *Reference is made in particular to the section [[Modulation_Methods/Error_Probability_of_Direct-Sequence_Spread_Spectrum_Modulation#Principle_of_the_rake_receiver |Principle of the rake receiver]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are valid for the channel impulse response $h_{\rm K}(t)$? |
|type="[]"} | |type="[]"} | ||
| − | + $h_{\rm K}(t)$ | + | + $h_{\rm K}(t)$ consists of two Dirac functions. |
| − | - $h_{\rm K}(t)$ | + | - $h_{\rm K}(t)$ is complex-valued. |
| − | - $h_{\rm K}(t)$ | + | - $h_{\rm K}(t)$ is a function periodic with delay time $\tau$. |
| − | { | + | {Which statements are true for the channel frequency response $H_{\rm K}(f)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $H_{\rm K}(f = 0) = 2$ is true. |
| − | + $H_{\rm K}(f)$ | + | + $H_{\rm K}(f)$ is complex-valued. |
| − | + $|H_{\rm K}(f)|$ | + | + $|H_{\rm K}(f)|$ is a function periodic with frequency $1/τ$. |
| − | { | + | {Set $K = 1$, $h_0 = 0.6$ and $h_1 = 0.4$. Determine the delays $τ_0$ and $τ_1$ so that the $h_{\rm KR}(t)$ equation is satisfied with $A_0 = A_2$. |
|type="{}"} | |type="{}"} | ||
$τ_0 \ = \ $ { 1 3% } $\ \rm µ s$ | $τ_0 \ = \ $ { 1 3% } $\ \rm µ s$ | ||
$τ_1 \ = \ $ { 0. } $\ \rm µ s$ | $τ_1 \ = \ $ { 0. } $\ \rm µ s$ | ||
| − | { | + | {What value should be chosen for the constant $K$? |
|type="{}"} | |type="{}"} | ||
$K \ = \ $ { 1.923 3% } | $K \ = \ $ { 1.923 3% } | ||
| − | { | + | {Which statements are valid for the signals $r(t)$ and $b(t)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The maximum value of $r(t)$ is $1$. |
| − | - | + | - The width of $r(t)$ is $7 \ µ s$. |
| − | - | + | - The maximum value of $b(t)$ is $1$. |
| − | + | + | + The width of $b(t)$ is $7 \ µ s$. |
| Line 67: | Line 67: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solution 1</u> is correct: |
| − | * | + | *The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when there is a dirac pulse at the input ⇒ $s(t) = δ(t)$. It follows that: |
:$$ h_(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$ | :$$ h_(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' <u>Solutions 2 and 3</u> are correct: |
| − | * | + | *By definition, the channel frequency response $H_{\rm K}(f)$ is the Fourier transform of the impulse response $h_{\rm K}(t)$. With the shift theorem this results in: |
:$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$ | :$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$ | ||
| − | * | + | *Accordingly, the first proposed solution is incorrect in contrast to the other two: $H_{\rm K}(f)$ is complex-valued and the magnitude is periodic with $1/τ$, as the following calculation shows: |
:$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$ | :$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$ | ||
| − | * | + | *For $f = 0$, $|H_{\rm K}(f)| = 1$. This value is repeated in the respective frequency spacing $1/τ$. |
Revision as of 11:57, 13 December 2021
The diagram shows a two-way channel (yellow background). The corresponding descriptive equation is:
- $$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$
Let the delay on the secondary path be $τ = 1 \ \rm µ s$. Drawn below is the structure of a rake receiver (green background) with general coefficients $K$, $h_0$, $h_1$, $τ_0$ and $τ_1$.
The purpose of the rake receiver is to combine the energy of the two signal paths, making the decision more reliable.
The combined impulse response of the channel and the rake receiver can be expressed in the form
- $$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$
but only if the rake coefficients $h_0$, $h_1$, $τ_0$ and $τ_1$ are appropriately chosen. The main part of $h_{\rm KR}(t)$ is supposed to be at $t = τ$.
The constant $K$ is to be chosen so that the amplitude of the main path $A_1 = 1$ :
- $$K= \frac{1}{h_0^2 + h_1^2}.$$
Apart from the rake parameters, the signals $r(t)$ and $b(t)$ are sought when $s(t)$ is a rectangle of height $s_0 = 1$ and width $T = \ \rm 5 µ s$.
Notes:
- The exercise belongs to the chapter Error Probability of Direct-Sequence Spread Spectrum Modulation.
- Reference is made in particular to the section Principle of the rake receiver.
Questions
Solution
- The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when there is a dirac pulse at the input ⇒ $s(t) = δ(t)$. It follows that:
- $$ h_(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$
(2) Solutions 2 and 3 are correct:
- By definition, the channel frequency response $H_{\rm K}(f)$ is the Fourier transform of the impulse response $h_{\rm K}(t)$. With the shift theorem this results in:
- $$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$
- Accordingly, the first proposed solution is incorrect in contrast to the other two: $H_{\rm K}(f)$ is complex-valued and the magnitude is periodic with $1/τ$, as the following calculation shows:
- $$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$
- For $f = 0$, $|H_{\rm K}(f)| = 1$. This value is repeated in the respective frequency spacing $1/τ$.
(3) Wir setzen zunächst vereinbarungsgemäß $K = 1$.
- Insgesamt kommt man über vier Wege von $s(t)$ zum Ausgangssignal $b(t)$.
- Um die vorgegebene $h_{\rm KR}(t)$–Gleichung zu erfüllen, muss entweder $τ_0 = 0$ gelten oder $τ_1 = 0$. Mit $τ_0 = 0$ erhält man für die Impulsantwort:
- $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$
- Um die „Hauptenergie” auf einen Zeitpunkt bündeln zu können, müsste dann $τ_1 = τ$ gewählt werden. Mit $h_0 = 0.6$ und $h_1 = 0.4$ erhält man dann $A_0 ≠ A_2$:
- $$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
- Dagegen ergibt sich mit $h_0 = 0.6$, $h_1 = 0.4$, $τ_0 = τ$ und $τ_1 = 0$:
- $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$
- Hier ist die Zusatzbedingung $A_0 = A_2$ erfüllt. Somit lautet das gesuchte Ergebnis:
- $$ \underline{\tau_0 = \tau = 1\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$
(4) Für den Normierungsfaktor muss gelten:
- $$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$
- Damit erhält man für die gemeinsame Impulsantwort $($es gilt $0.24/0.52 = 6/13)$:
- $$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
(5) Richtig sind die Aussagen 1 und 4, wie die Grafik zeigt:
- Für das Empfangssignal $r(t)$ und für das Rake–Ausgangssignal $b(t)$ gilt:
- $$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm µ s})\hspace{0.05cm},$$
- $$b(t) = \frac{6}{13} \cdot s(t) + 1 \cdot s (t - 1\,{\rm µ s}) + \frac{6}{13} \cdot s (t - 2\,{\rm µ s}) \hspace{0.05cm}.$$
- Die Überhöhung des Ausgangssignals ⇒ $b(t) > 1$ ist auf den Normierungsfaktor $K = 25/13$ zurückzuführen.
- Mit $K = 1$ wäre der Maximalwert von $b(t)$ tatsächlich $1$.