Aufgaben:Exercise 5.4: Comparison of Rectangular and Hanning Window

• Return to book

Gegeben sei der prinzipielle Zeitverlauf x(t) eines periodischen Signals. Unbekannt sind die Parameter A1, f1, A2 und f2:

$$x(t) & = & A_1 \cdot \cos (2 \pi \cdot f_1 \cdot t)+\\ & + & A_2 \cdot \cos (2 \pi \cdot f_2 \cdot t) \hspace{0.05cm}.$$

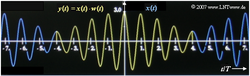
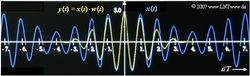
Nach Gewichtung des Signals mit dem Fenster w(t) wird das Produkt y(t) = x(t) · w(t) einer Diskreten Fouriertransformation (DFT) mit den Parametern N = 512 und TP unterworfen. Die Zeitdauer TP des analysierten Signalausschnitts kann vom Benutzer beliebig eingestellt werden. Für die Fensterung stehen folgende Funktionen zur Verfügung, die jeweils für |t| > TP/2 identisch 0 sind: das Rechteckfenster:

$${w} (\nu) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}, \\ \end{array}$$

$$W(f) ={1}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot {f}/{f_{\rm A}})\hspace{0.05cm},$$

das Hanning–Fenster:

$${w} (\nu) = \left\{ \begin{array}{c} 0.5 + 0.5 \cdot \cos (2 \pi \cdot \frac{\nu}{N}) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ \\ \end{array}\begin{array}{*{20}c} -N/2 \le \nu < N/2 \hspace{0.05cm}, \\ {\rm sonst} \hspace{0.05cm}, \\ \end{array}$$

$$W(f) ={0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f}{f_{\rm A}})+ {0.25}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f-f_{\rm A}}{f_{\rm A}})+ {0.5}/{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$

Beachten Sie, dass die Frequenzauflösung fA gleich dem Kehrwert des einstellbaren Parameters TP ist. W(f) ist die Fouriertransformierte der zeitkontinuierlichen Fensterfunktion w(t), während die oben angegebene Funktion w(ν) die zeitdiskrete Gewichtungsfunktion angibt. Im Laufe der Aufgabe wird auf verschiedene Spektralfunktionen Y(f) Bezug genommen, zum Beispiel auf

$$Y_{\rm A}(f) = 1\, {\rm V}\cdot {\rm \delta} (f \pm 1\,\,{\rm kHz})+ 0.5\,\, {\rm V}\cdot {\rm \delta} (f \pm 1.125\,\,{\rm kHz}) \hspace{0.05cm}.$$

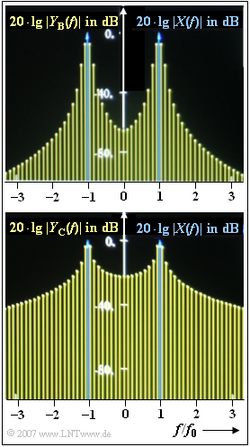
In der obigen Grafik sind zwei weitere Spektralfunktionen YB(f) und YC(f) abgebildet, die sich ergeben, wenn ein 1 kHz–Signal mittels DFT analysiert wird und der DFT–Parameter TP = 8.5 ms ungünstig gewählt ist. Für eines der Bilder ist das Rechteckfenster zugrundegelegt, für das andere das Hanning–Fenster. Nicht angegeben wird, welche Spektralfunktion zu welchem Fenster gehört. Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 5.4.

Fragebogen

1

Welche der folgenden Aussagen treffen mit Sicherheit zu, wenn die DFT das Ausgangsspektrum YA(f) anzeigt?

	Zur Gewichtung wurde das Rechteckfenster verwendet.
	Zur Gewichtung wurde das Hanning–Fenster verwendet.
	Es wurde der DFT–Parameter TP = 4 ms verwendet.
	Das DFT–Spektrum YA(f) ist identisch mit dem Spektrum X(f).

2

Wie lautet Y(f) bei Verwendung des Hanning–Fensters und TP = 8 ms, wenn das Eingangsspektrum X(f) = YA(f) anliegt? Geben Sie die Gewichte der Diraclinien bei f1 = 1 kHz und f2 = 1.125 kHz an.

$G(f_1 = 1 \text{kHz}) =$ V

$G(f_1 = 1.125 \text{kHz}) =$ V

3

Wir betrachten das 1 kHz–Cosinussignal x(t). Welches Spektrum – YB(f) oder YC(f) – ergibt sich mit dem Rechteck– bzw. dem Hanning–Fenster, wenn der DFT-Parameter TP = 8.5 ms ungünstig gewählt ist?

	YB(f) ergibt sich bei Rechteckfensterung.
	YB(f) ergibt sich mit dem Hanning-Fenster.

Musterlösung

Solution

1. a) Bei Verwendung des Hanning–Fensters müssten zunächst 3 Diracfunktionen zu erkennen sein, auch wenn x(t) nur eine Frequenz beinhaltet ⇒ es wurde das Rechteckfenster verwendet. Mit TP = 4 ms ergibt sich für die Frequenzauflösung fA = 1/TP = 0.25 kHz. Damit liegt die Frequenz f2 nicht im vorgegebenen Raster und Y(f) würde sich aus sehr vielen Diraclinien zusammensetzen. Das heißt: die dritte Aussage ist falsch. Wie aus der nachfolgenden Grafik hervorgeht, hat x(t) die Periodendauer T0 = 8 ms. Wählt man den DFT–Parameter gleich TP = 8 ms (oder ein ganzzahliges Vielfaches davon), so stimmt die periodische Fortsetzung P{x(t)} im Intervall |t| ≤ TP/2 mit x(t) überein, so dass sich die Gewichtungsfunktion w(t) nicht störend auswirkt: Das DFT–Spektrum Y(f) stimmt somit mit dem tatsächlichen Spektrum überein. Richtig sind somit die Lösungsvorschläge 1 und 4.

b) Wegen TP = 8 ms setzt sich das Hanning–Spektrum W(f) aus drei Diracfunktionen bei positiven Frequenzen und drei dazu achsensymmetrischen Diracs bei negativen Frequenzen zusammen. Für die positiven Frequenzen lautet die Spektralfunktion:

$$W(f) =0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm \delta}(f-f_{\rm A})+ 0.25\cdot {\rm \delta}(f+f_{\rm A})\hspace{0.05cm}.$$

Das Ausgangsspektrum ergibt sich aus der Faltung zwischen X(f) und W(f). Bei positiven Frequenzen ergeben sich nun vier Diracs mit folgenden Gewichten:

$$G(f = 0.875\,{\rm kHz}) & = & 1\, {\rm V}\cdot 0.25 = 0.250\, {\rm V}, \\ G(f = f_1 = 1.000\,{\rm kHz}) & = & 1\, {\rm V}\cdot 0.5 + 0.5\, {\rm V}\cdot 0.25 \hspace{0.15 cm}\underline{ = 0.625\, {\rm V}}, \\ G(f = f_2 = 1.125\,{\rm kHz}) & = & 1\, {\rm V}\cdot 0.25 + 0.5\, {\rm V}\cdot 0.5 \hspace{0.15 cm}\underline{= 0.500\, {\rm V}}, \\ G(f = 1.250\,{\rm kHz}) & = & 0.5\, {\rm V}\cdot 0.25 = 0.125\, {\rm V} \hspace{0.05cm}.$$

Die folgende Grafik zeigt die Abschwächung der Ränder durch die Gewichtungsfunktion w(t) des Hanning–Fensters.

c) Das Rechteck–Fenster liefert dann ein sehr stark verfälschtes Ergebnis, wenn die Fensterbreite TP (wie hier) nicht an die Frequenz des Cosinussignals angepasst ist. In diesem Fall ist das Hanning–Fenster besser geeignet. Daraus folgt: Richtig ist der zweite Lösungsvorschlag.