Difference between revisions of "Theory of Stochastic Signals/Generation of Discrete Random Variables"
| Line 87: | Line 87: | ||
*Here it is to be considered that in the modulo-2 algebra $+1$ and $-1$ are identical. }} | *Here it is to be considered that in the modulo-2 algebra $+1$ and $-1$ are identical. }} | ||
| − | == | + | ==Reciprocal polynomials== |
<br> | <br> | ||
| − | {{ | + | {{BlueBox|TEXT= |
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | The '''reciprocal polynomial''' associated with the generator polynomial $G(D)$ is: | |
:$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$}} | :$$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$}} | ||
| − | + | Between the two shift registers with polynomials $G(D)$ and $G_{\rm R}(D)$ respectively, there are the following relations: | |
| − | * | + | *If $G(D)$ provides a sequence of maximum length ⇒ $P_{\rm max} = 2^L - 1$, then the period length of the reciprocal polynomial $G_{\rm R}(D)$ is also maximum. |
| − | * | + | *The output sequences of reciprocal configurations are inverses of each other That is: |
| − | * | + | *The sequence of $G(D)$ - read from right to left - gives the sequence of the reciprocal configuration $G_{\rm R}(D)$. |
| − | In [[Theory_of_Stochastic_Signals/ | + | In [[Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables#Sequences_of_maximum_length_.28M-sequences.29 |above table]] the reciprocal polynomials associated to $G(D)$ are given in the third column $G_{\rm R}(D)$ up to register degree $L = 31$ . |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | We again consider the degree $L = 4$. | |
| − | * | + | *Based on the shift register structure $(31)_{\rm oct}$ we obtain for the reciprocal polynomial. |
| − | :$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} | + | :$$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$ |
| − | : | + | :and thus the configuration with the octal identifier $(23)$. |
| − | * | + | *The corresponding output sequences each have the maximum period length $P_{\rm max} = 15$ and are inverses of each other: |
| − | ** ... $0 \ 0 | + | ** ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ... |
| − | ** ... $0 | + | ** ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ... |
| − | * | + | *This means that the upper initial sequence of $(31)$, read from right to left, yields the sequence of reciprocal order $(23)$ given below. |
| − | * | + | *However, a cyclic phase shift of four binary digits can be seen. }} |
| − | + | The topic of this chapter is illustrated with examples in the (German language) learning video [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN-Generatoren an einem Beispiel]] $\Rightarrow$ Explanation of PN generators by example. | |
Revision as of 21:38, 19 December 2021
Contents
Pseudorandom variables
One way to generate a binary random sequence $〈z_{\rm ν}〉 ∈ \{0, 1\}$ with good statistical properties is offered by the so-called pseudorandom generators, also known as PN generators, where "PN" stands for pseudonoise .
These have the following properties:
- The binary sequence generated by such a generator is not stochastic in a strict sense, but exhibits periodic and thus deterministic properties.
- If the period length $P$ is sufficiently large, the sequence appears to an observer as random with sufficiently good statistical properties for many applications.
- The advantage of a pseudorandom generator over a "real" stochastic source is that the random sequence is reproducible if a few parameters are known.
$\text{Example 1:}$ The latter property also gives rise to the main applications of pseudo-noise generators:
- first, the error frequency measurement in digital signal transmission,
- secondly, for band spreading in CDMA (Code Division Multiple Access).
In such a Spread Spectrum System the transmit signal is modulated with a binary random sequence, whose symbol repetition frequency is significantly higher than the bit frequency. This offers the possibility of multiple channel utilization. Since the same sequence must be added in phase at the receiver, the use of reproducible PN sequences is also common here.
Detailed information on bandspreading methods can be found in the chapter UMTS - Universal Mobile Telecommunications System of the German book "Beispiele von Nachrichtensystemen" .
Realization of PN generators
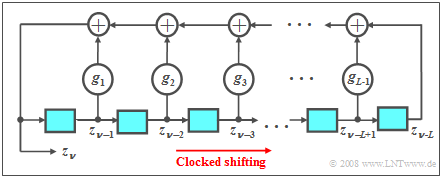
Pseudorandom generators are usually realized by feedback shift registers, where at each clock instant the content of the register is shifted one place to the right (see diagram). For the currently generated symbol, with $g_l ∈ \{0, 1\}$ and $l = 1$, ... , $L-1$:
- $$z_\nu = (g_1\cdot z_{\nu-1}+g_2\cdot z_{\nu-2}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_l\cdot z_{\nu-l}+\hspace{0.1cm}\text{...}\hspace{0.1cm}+g_{L-1}\cdot z_{\nu-L+1}+ z_{\nu-L})\hspace{0.1cm} \rm mod \hspace{0.2cm}2.$$
- The binary values $z_{ν-1}$ to $z_{ν-L}$ generated at previous time points are stored in the memory cells of the shift register.
- The coefficients $g_1$, ... , $g_{L-1}$ are also binary values, where a $1$ indicates a feedback at the corresponding location and a $0$ indicates no feedback.
- Modulo-2 addition can be implemented, for example, using an XOR operation:
- $$(x + y)\hspace{0.1cm} \rm mod\hspace{0.1cm}2 = \it x\hspace{0.1cm}\rm XOR\hspace{0.1cm} \it y = \left\{\begin{array}{*{2}{c}} \rm 0 & \rm falls\hspace{0.1cm} \it x= y,\rm 1 & \rm falls\hspace{0.1cm} \it x\neq y. \end{array} \right.$$
The statistical properties of the generated pseudonoise random sequence $〈z_{\rm ν}〉$ are essentially determined by.
- the degree $L$, and
- the feedback coefficients $g_{\hspace{0.05cm}l}$ $($with $l = 1$, ... , $L-1)$.
A prerequisite for the generation of a PN sequence is that not all memory elements are preallocated with zeros, otherwise the modulo-2 addition would always generate only the symbol $0$ .
To identify different PN generators one uses in the literature alternatively:
- the so-called generator polynomials of the type.
- $$G(D) = g_L\cdot D^L+g_{L-1}\cdot D^{L-1}+ \ \text{...} \ +g_1\cdot D+g_0 .$$
- Here, always $g_0 = g_L = 1$ to be set and $D$ a formal parameter indicating a delay by one clock $(D^L$ indicates a delay by $L$ clocks$)$;
- the octal representation of the binary number $(g_L\ \text{ ...} \ g_2 \ g_1 \ g_0)$. It is important that here the feedback coefficients - starting from the right with $g_0$ - are combined into triples and these are written octal $(0 \ \text{...}\ 7)$.
$\text{Example 2:}$ The generator polynomial $D^4 + D^3 + 1$ belongs to a shift register of degree $L = 4$ with the following octal representation.
- $$(g_4 \ g_3 \ g_2 \ g_1 \ g_0) = (11001)_{\rm bin} = (31)_{\rm oct}. $$
Sequences of maximum length (M-sequences)
If not all $L$ memory cells of the shift register are preallocated with zeros, a periodic random sequence $〈z_ν\rangle$ always results:
- The period length $P$ of this sequence depends to a strong degree on the feedback coefficients.
- For each degree $L$ there is at least one configuration with the maximum period length
- $$P_{\rm max} = \rm 2^{\it L}-\rm 1.$$
Such a PN sequence is also often referred to as a $\rm M-sequence$, where the $\rm M$ stands for "Maximum".
$\text{For now, without proof:}$
- A $\rm M-sequence$ can be recognized by the fact that the generator polynomial $G(D)$ is primitive.
- As detailed in the book Channel Coding , a polynomial $G(D)$ of degree $L$ is called primitive if the following condition is satisfied:
- $$\frac{(D^n+\rm 1)}{\it G(D)} \neq 0\hspace{0.5cm} {\rm for}\hspace{0.5cm}\it n<P_{\rm max} \rm = \rm 2^{\it L}-\rm 1.$$
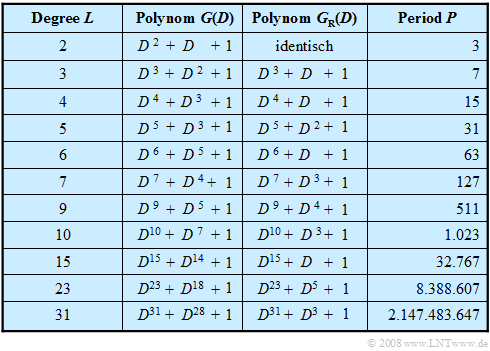
The table lists PN generators of maximum length up to degree $L = 31$ .
- The selection is limited to configurations with only one tap - that is, with two returns.
- This means that the associated polynomials consist of only three summands.
- For applications that require high speed, such generators are very useful.
$\text{Example 3:}$ A shift register of degree $L = 4$ with octal identifier $(31)$ and generator polynomial $G(D) = D^4 + D^3 + 1$ leads to a sequence of maximum length:
- $$P_{\rm max} = 2^4 - 1 = 15.$$
The mathematical proof for this is complex:
- Using the above polynomial division for $n = 1$, ... , $14$ one must show that the quotient is always nonzero.
- First the division $(D^{15} + 1)/G(D)$ may give a result without remainder.
- Here it is to be considered that in the modulo-2 algebra $+1$ and $-1$ are identical.
Reciprocal polynomials
$\text{Definition:}$ The reciprocal polynomial associated with the generator polynomial $G(D)$ is:
- $$G_{\rm R}(D)=D^{L}\cdot G(D^{-1}).$$
Between the two shift registers with polynomials $G(D)$ and $G_{\rm R}(D)$ respectively, there are the following relations:
- If $G(D)$ provides a sequence of maximum length ⇒ $P_{\rm max} = 2^L - 1$, then the period length of the reciprocal polynomial $G_{\rm R}(D)$ is also maximum.
- The output sequences of reciprocal configurations are inverses of each other That is:
- The sequence of $G(D)$ - read from right to left - gives the sequence of the reciprocal configuration $G_{\rm R}(D)$.
In above table the reciprocal polynomials associated to $G(D)$ are given in the third column $G_{\rm R}(D)$ up to register degree $L = 31$ .
$\text{Example 4:}$ We again consider the degree $L = 4$.
- Based on the shift register structure $(31)_{\rm oct}$ we obtain for the reciprocal polynomial.
- $$G_{\rm R}(D) = D^{\rm 4}\cdot (1+D^{-3} + D^{ -4})=D^{ 4}+D^{1}+\rm 1$$
- and thus the configuration with the octal identifier $(23)$.
- The corresponding output sequences each have the maximum period length $P_{\rm max} = 15$ and are inverses of each other:
- ... $0 \ 0 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- ... $0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1$ ...
- This means that the upper initial sequence of $(31)$, read from right to left, yields the sequence of reciprocal order $(23)$ given below.
- However, a cyclic phase shift of four binary digits can be seen.
The topic of this chapter is illustrated with examples in the (German language) learning video Erläuterung der PN-Generatoren an einem Beispiel $\Rightarrow$ Explanation of PN generators by example.
Erzeugung mehrstufiger Zufallsgrößen
Viele höhere Programmiersprachen bieten Pseudo-Zufallsgeneratoren an, die reelle, zwischen $0$ und $1$ gleichverteilte Zufallszahlen $x$ liefern. Beispielsweise lautet ein entsprechender C-Funktionsaufruf:
- $$x = \text{random()}.$$
Durch sukzessives Aufrufen der "Random-Funktion" entsteht eine periodisch sich wiederholende Folge reeller Zahlen, wobei alle Funktionswerte $0 \le x < 1$ gleichwahrscheinlich sind ⇒ siehe Kapitel Gleichverteilte Zufallsgrößen.
- Da die Periodendauer $P$ jedoch sehr groß ist, kann diese Folge als pseudozufällig angesehen werden.
- Durch Angabe eines Startwertes wird an bestimmten Stellen der Pseudozufallsfolge begonnen.
Bei der Generierung einer wertdiskreten mehrstufigen Zufallsgröße $z$ wird zweckmäßigerweise von einer solchen gleichverteilten Zufallsgröße $x$ ausgegangen.
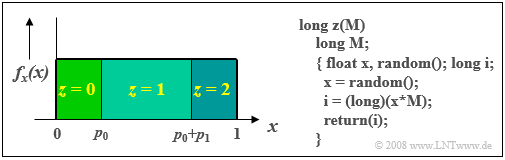
$\text{Beispiel 5:}$ Die Grafik zeigt das Prinzip für den Sonderfall $M = 3$, wobei die gewünschten Auftrittswahrscheinlichkeiten mit $p_0$, $p_1$ und $p_2$ bezeichnet sind.
Dann gilt:
- Ist der aktuelle Wert $x$ der zwischen $0$ und $1$ gleichverteilten Zufallsgröße kleiner als $p_0$, so wird die ternäre Zufallsgröße $z = 0$ gesetzt.
- Im Bereich $p_0 ≤ x < p_0 + p_1$ wird $z = 1$ ausgegeben.
- Für $x \ge p_0 + p_1$ wird die Zufallsgröße zu $z =2$.
Im aufgeführten C-Programm ergibt sich für $M = 3$ und für den aktuellen Zufallswert $x = 0.57$ für das Produkt $x · M = 0.57 · 3 = 1.71$ und somit die diskrete Zufallsgröße $z = 1$. Für einen zweiten Zufallswert $x = 0.95$ würde die Funktion dagegen das Ergebnis $z = 2$ liefern.
Aus Verständnisgründen wurde hier eine umständliche Programmierung gewählt. Der angegebene C-Programmteil könnte auch kompakter geschrieben werden:
- $$\text{\{ float random(); return((long) (random()*M)); \} }$$
Aufgaben zum Kapitel
Aufgabe 2.6: PN-Generator der Länge 5
Aufgabe 2.6Z: PN-Generator der Länge 3
Aufgabe 2.7: C-Programme z1 und z2
Zusatzaufgabe 2.7Z: C-Programm z3