Difference between revisions of "Exercise 2.6Z: PN Generator of Length 3"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables |
}} | }} | ||
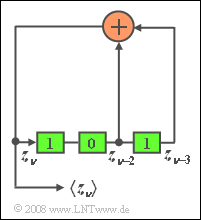
| − | [[File:P_ID106__Sto_Z_2_6.png|right|frame|PN | + | [[File:P_ID106__Sto_Z_2_6.png|right|frame|PN generator with $L = 3$]] |
| − | + | The adjacent sketch shows a PN generator of length $L = 3$ with generator polynomial | |
:$$G( D) = D^{\rm 3} + D^{\rm 2} + \rm 1$$ | :$$G( D) = D^{\rm 3} + D^{\rm 2} + \rm 1$$ | ||
| − | + | and thus the octal identifier $(g_3 \ g_2 \ g_1 \ g_0)$ = $(1 \ 1 \ 0 \ 1)_{\rm bin} = (15)_{\rm oct}$. | |
| − | + | The corresponding reciprocal polynomial | |
| − | :$$G_{\rm R}(D) = | + | :$$G_{\rm R}(D) = D^{\rm 3}\cdot ( D^{\rm -3} + D^{\rm -2} + 1) = D^{\rm 3} + D^{\rm 1} + \rm 1$$ |
| − | + | has the octal identifier $(1 \ 0 \ 1 \ 1)_{\rm bin} = (13)_{\rm oct}$. | |
| − | * | + | *At start time, let the three memory cells be preallocated with the binary values $1$, $0$ and $1$ . |
| − | * | + | *Both arrangements generate an M sequence. |
| Line 22: | Line 22: | ||
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables|Generation of Discrete Random Variables]]. | |
| − | * | ||
| − | * | + | *The topic of this chapter is illustrated with examples in the (German language) learning video [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|Erläuterung der PN-Generatoren an einem Beispiel]] $\Rightarrow$ Explanation of PN generators by example. |
| Line 33: | Line 32: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How long is the period length of the configuration $(15)$? |
|type="{}"} | |type="{}"} | ||
$P \ = \ $ { 7 } | $P \ = \ $ { 7 } | ||
| − | { | + | {Determine the output sequence $〈z_ν\rangle$ for the time points $1$, ... , $P$. What are the first $15$ binary values of the output sequence? <br>''Hint:'' From left to right, label the cells with $S_1$, $S_2$ and $S_3$. Output the value $z_ν$ that is currently $\nu$ entered into the memory cell $S_1$ . |
|type="()"} | |type="()"} | ||
- $1\ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1 \ 0 \ 0 \ 0$ . . . | - $1\ 0 \ 0 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 1 \ 0 \ 0 \ 0$ . . . | ||
- $1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 $ . . . | - $1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 $ . . . | ||
+ $1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1$ . . . | + $1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1$ . . . | ||
| − | - $0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 | + | - $0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 $. . . |
| − | { | + | {Which of the following statements are true for each M sequence? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The number of zeros and ones is equal. |
| − | + In | + | + In each period there is one more one than zeros. |
| − | + | + | + The maximum number of consecutive ones is $L$. |
| − | + | + | + The sequence $1 \ 0 \ 1 \ 0 \ 1 \ 0 $ ... is not possible. |
| − | { | + | {Now consider the reciprocal order $(13)$. What are the first $15$ binary values of the initial sequence with the same initial assignment here? |
|type="()"} | |type="()"} | ||
| − | - $0 \ | + | - $0 \ 0 \ 0 \ 1 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 $ . . . |
| − | + $0 | + | + $0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1 \ 1 \ 0 \ 1 \ 0 $ . . . |
| − | - $0 | + | - $0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \ 1 \ 0 $ . . . |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
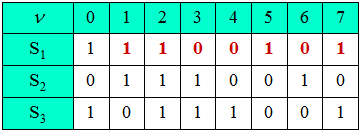
| − | [[File:EN_Sto_Z_2_6b.png|right|frame|PN– | + | [[File:EN_Sto_Z_2_6b.png|right|frame|PN–generator with octal identifier $15$]] |
| − | '''(1)''' | + | '''(1)''' It is an M-sequence with $L= 3$. It follows that $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$. |
| − | '''(2)''' | + | '''(2)''' We denote the cells from left to right by $S_1$, $S_2$ and $S_3$. Then holds: |
* $S_2(\nu) = S_1(\nu - 1)$, | * $S_2(\nu) = S_1(\nu - 1)$, | ||
| Line 75: | Line 74: | ||
| − | + | The result is entered in the first row of the above table (marked in red): | |
| − | * | + | *At the clock time $\nu = 7$ results in the same memory usage as at the time $\nu = 0$. |
| − | * | + | *From this follows $ {P = 7}$ and the sequence is from $\nu = 1$ corresponding to <u>solution 3</u> : |
| − | :$$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 | + | :$$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \text{...}$$ |
| − | * | + | *In contrast, proposal 1 describes the M sequence of the PN generator with length $L=4$ and identifier $(31)$ ⇒ period length is $P= 15$. |
| − | * | + | *In proposal 2, the period length $P= 4$ is too short. |
| − | * | + | *Finally, the last proposal would have the desired period length $P= 7$, but from the modulo 2 addition of $S_2= 0$ and $S_3= 1$ $($für $\nu = 0)$ it necessarily follows at the next time $(\nu = 1)$ : $S_1= 1$. This property is not exhibited by sequence 4. |
| − | '''(3)''' | + | '''(3)''' Correct are <u>solutions 2, 3, and 4</u>: |
| − | * | + | *The maximum number of consecutive ones is $L$ (namely if there is a one in all $L$ memory cells). |
| − | * | + | *On the other hand, it is not possible that all memory cells are filled with zeros. Therefore, there is always one more than zeros. |
| − | * | + | *The period length of the last sequence is $P = 2$. On the other hand, for an M-sequence $P= 2^L - 1.$ For no value of $L$ is $P = 2$ possible. |
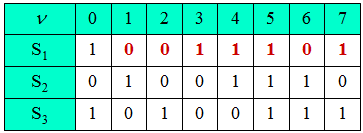
| − | [[File: EN_Sto_Z_2_6d.png|right|frame|PN– | + | [[File: EN_Sto_Z_2_6d.png|right|frame|PN–generator with octal identifier $13$]] |
| − | '''(4)''' In | + | '''(4)''' In the adjacent table the emergence of the PN–sequence at the reciprocal polynomial $G_{\rm R}(D)$ is entered. |
| − | + | It can be seen that the <u>proposed solution 2</u> applies: | |
| − | * | + | *Also for the reciprocal arrangement, the period length $P = 7$ must hold, so that proposition 1 $($with $P = 15)$ is eliminated. |
| − | * | + | *Proposal 3 is just a version of the initial sequence of $(15)$ shifted by two clocks. |
| − | * | + | *In contrast, in the (correct) second proposal, the inverse of ... $ 1 \ 1 \ 0 \ 1 \ 0 \ 1$ ... – thus the sequence ... $ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – are included, albeit with a phase shift. |
Revision as of 09:42, 21 December 2021
The adjacent sketch shows a PN generator of length $L = 3$ with generator polynomial
- $$G( D) = D^{\rm 3} + D^{\rm 2} + \rm 1$$
and thus the octal identifier $(g_3 \ g_2 \ g_1 \ g_0)$ = $(1 \ 1 \ 0 \ 1)_{\rm bin} = (15)_{\rm oct}$.
The corresponding reciprocal polynomial
- $$G_{\rm R}(D) = D^{\rm 3}\cdot ( D^{\rm -3} + D^{\rm -2} + 1) = D^{\rm 3} + D^{\rm 1} + \rm 1$$
has the octal identifier $(1 \ 0 \ 1 \ 1)_{\rm bin} = (13)_{\rm oct}$.
- At start time, let the three memory cells be preallocated with the binary values $1$, $0$ and $1$ .
- Both arrangements generate an M sequence.
Hints:
- The exercise belongs to the chapter Generation of Discrete Random Variables.
- The topic of this chapter is illustrated with examples in the (German language) learning video Erläuterung der PN-Generatoren an einem Beispiel $\Rightarrow$ Explanation of PN generators by example.
Fragebogen
Solution
(1) It is an M-sequence with $L= 3$. It follows that $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$.
(2) We denote the cells from left to right by $S_1$, $S_2$ and $S_3$. Then holds:
- $S_2(\nu) = S_1(\nu - 1)$,
- $S_3(\nu) = S_2(\nu - 1)$,
- $S_1(\nu) = S_2(\nu - 1) \ {\rm mod } \ S_3(\nu - 1)$.
The result is entered in the first row of the above table (marked in red):
- At the clock time $\nu = 7$ results in the same memory usage as at the time $\nu = 0$.
- From this follows $ {P = 7}$ and the sequence is from $\nu = 1$ corresponding to solution 3 :
- $$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \text{...}$$
- In contrast, proposal 1 describes the M sequence of the PN generator with length $L=4$ and identifier $(31)$ ⇒ period length is $P= 15$.
- In proposal 2, the period length $P= 4$ is too short.
- Finally, the last proposal would have the desired period length $P= 7$, but from the modulo 2 addition of $S_2= 0$ and $S_3= 1$ $($für $\nu = 0)$ it necessarily follows at the next time $(\nu = 1)$ : $S_1= 1$. This property is not exhibited by sequence 4.
(3) Correct are solutions 2, 3, and 4:
- The maximum number of consecutive ones is $L$ (namely if there is a one in all $L$ memory cells).
- On the other hand, it is not possible that all memory cells are filled with zeros. Therefore, there is always one more than zeros.
- The period length of the last sequence is $P = 2$. On the other hand, for an M-sequence $P= 2^L - 1.$ For no value of $L$ is $P = 2$ possible.
(4) In the adjacent table the emergence of the PN–sequence at the reciprocal polynomial $G_{\rm R}(D)$ is entered. It can be seen that the proposed solution 2 applies:
- Also for the reciprocal arrangement, the period length $P = 7$ must hold, so that proposition 1 $($with $P = 15)$ is eliminated.
- Proposal 3 is just a version of the initial sequence of $(15)$ shifted by two clocks.
- In contrast, in the (correct) second proposal, the inverse of ... $ 1 \ 1 \ 0 \ 1 \ 0 \ 1$ ... – thus the sequence ... $ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – are included, albeit with a phase shift.