Difference between revisions of "Aufgaben:Exercise 2.6: PN Generator of Length 5"
From LNTwww
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sto_A_2_6.png|right|frame|PN generator of length $L = 5$]] |
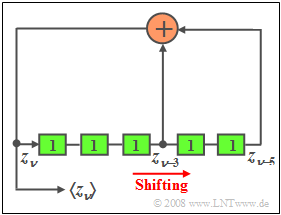
| − | In | + | In the graphic you can see a pseudo-random generator of length $L = 5$, which can be used to generate a binary random sequence $\langle z_{\nu} \rangle$. |
| − | * | + | *At the start time, let all memory cells be preallocated with "ones". |
| − | * | + | *At each clock time, the content of the shift register is shifted one place to the right. |
| + | * And the currently generated binary value $z_{\nu}$ $(0$ or $1)$ is entered into the first memory cell. | ||
| + | *Hereby $z_{\nu}$ results from the modulo-2 addition between $z_{\nu-3}$ and $z_{\nu-5}$. | ||
| − | |||
| Line 16: | Line 17: | ||
| − | + | Hints: | |
| − | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Generation_of_Discrete_Random_Variables|Generation of Discrete Random Variables]]. | |
| − | * | ||
| − | * | + | *The topic of this chapter is illustrated with examples in the (German language) learning video: <br> [[Erläuterung_der_PN–Generatoren_an_einem_Beispiel_(Lernvideo)|"Erläuterung der PN-Generatoren an einem Beispiel"]] $\Rightarrow$ "Explanation of PN generators using an example". |
| − | === | + | ===Question=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the generator polynomial $G(D)$ of the PN generator shown? |
|type="()"} | |type="()"} | ||
- $G(D) = D^5 + D^2 +1$. | - $G(D) = D^5 + D^2 +1$. | ||
| Line 33: | Line 33: | ||
| − | { | + | {What octal identifier $O_{\rm G}$ does this PN generator have? |
|type="{}"} | |type="{}"} | ||
| − | $O_{\rm G} \ = \ $ | + | $O_{\rm G} \ = \ $ { 51 } $\ \rm (octal)$ |
| − | { | + | {Assume that the generator polynomial $G(D)$ is primitive. <br>Is the initial sequence $〈z_ν \rangle$ an M-sequence? How large is the period $P$? |
|type="{}"} | |type="{}"} | ||
| − | $P\ = | + | $P\ = \ $ { 31 } |
| − | { | + | {What octal identifier $O_{\rm R}$ describes the polynomial $G_{\rm R}(D)$ reciprocal to $G(D)$? |
|type="{}"} | |type="{}"} | ||
| − | $O_{\rm R} \ = \ $ { 45 } $\ \rm ( | + | $O_{\rm R} \ = \ $ { 45 } $\ \rm (octal)$ |
| − | { | + | {What statements hold for the configuration with the polynomial $G_{\rm R}(D)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It is also a sequence of maximum length. |
| − | - | + | - The output sequence of $G_{\rm R}(D)$ is the same as that of the generator polynomial $G(D)$. |
| − | + | + | + The output sequences of $G_{\rm R}(D)$ and $G(D)$ are inverses of each other. |
| − | + | + | + Both sequences show the same statistical properties. |
| − | - | + | - In $G_{\rm R}(D)$ all memory elements can be preallocated with zeros. |
| Line 60: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>proposed solution 2</u> ⇒ $G(D) = D^5 + D^3 +1$. |
| − | * | + | *The generator polynomial $G(D)$ denotes the feedback coefficients used for modulo-2 addition. |
| − | *$D$ | + | *$D$ is a formal parameter indicating a delay by one clock. |
| − | *$D^3$ | + | *$D^3$ then indicates a delay of three measures. |
| − | '''(2)''' | + | '''(2)''' It is $g_0 = g_3 = g_5 = 1$. |
| − | * | + | *All other feedback coefficients are $0$. It follows that: |
:$$(g_{\rm 5}\hspace{0.1cm}g_{\rm 4}\hspace{0.1cm}g_{\rm 3}\hspace{0.1cm}g_{\rm 2}\hspace{0.1cm}g_{\rm 1}\hspace{0.1cm}g_{\rm 0})=\rm (101001)_{bin}\hspace{0.15cm} \underline{=(51)_{oct}}.$$ | :$$(g_{\rm 5}\hspace{0.1cm}g_{\rm 4}\hspace{0.1cm}g_{\rm 3}\hspace{0.1cm}g_{\rm 2}\hspace{0.1cm}g_{\rm 1}\hspace{0.1cm}g_{\rm 0})=\rm (101001)_{bin}\hspace{0.15cm} \underline{=(51)_{oct}}.$$ | ||
| − | '''(3)''' | + | '''(3)''' Since the generator polynomial $G(D)$ is primitive, one obtains an "M-sequence". |
| − | * | + | *Accordingly, the period is maximal: |
:$$P_{\rm max} = 2^{L}-1 \hspace{0.15cm}\underline {= 31}.$$ | :$$P_{\rm max} = 2^{L}-1 \hspace{0.15cm}\underline {= 31}.$$ | ||
| − | * | + | *In the theory part, the table with PN generators of maximum length ("M-sequences") for degree $L=5$ lists the configuration $(51)_{\rm oct}$. |
| − | '''(4)''' | + | |
| + | '''(4)''' The reciprocal polynomial is: | ||
:$$G_{\rm R}(D)=D^{\rm 5}\cdot(D^{\rm -5}+\D^{\rm -3}+ 1)= D^{\rm 5}+D^{\rm 2}+1.$$ | :$$G_{\rm R}(D)=D^{\rm 5}\cdot(D^{\rm -5}+\D^{\rm -3}+ 1)= D^{\rm 5}+D^{\rm 2}+1.$$ | ||
| − | * | + | *Thus, the octal identifier für this configuration: $\rm (100101)_{bin}\hspace{0.15cm} \underline{=(45)_{oct}}.$ |
| + | |||
| + | '''(5)''' The <u>solutions 1, 3, and 4</u> are correct: | ||
| + | *The output sequence of the reciprocal realization $G_{\rm R}(D)$ of a primitive polynomial $G(D)$ is also an "M-sequence". | ||
| + | *Both sequences are inverses of each other. This means: | ||
| + | *The output sequence of $(45)_{\rm oct}$ is equal to the output sequence of $(51)_{\rm oct}$ when read from right to left, additionally taking into account a phase ("cyclic shift"). | ||
| + | *The prerequisite is again that not all memory cells are preallocated with zeros. | ||
| + | *Under this condition, both sequences actually have the same statistical properties. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 100: | Line 102: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^2.5 Generation of Discrete Random Variables^]] |
Latest revision as of 16:04, 28 December 2021
In the graphic you can see a pseudo-random generator of length $L = 5$, which can be used to generate a binary random sequence $\langle z_{\nu} \rangle$.
- At the start time, let all memory cells be preallocated with "ones".
- At each clock time, the content of the shift register is shifted one place to the right.
- And the currently generated binary value $z_{\nu}$ $(0$ or $1)$ is entered into the first memory cell.
- Hereby $z_{\nu}$ results from the modulo-2 addition between $z_{\nu-3}$ and $z_{\nu-5}$.
Hints:
- The exercise belongs to the chapter Generation of Discrete Random Variables.
- The topic of this chapter is illustrated with examples in the (German language) learning video:
"Erläuterung der PN-Generatoren an einem Beispiel" $\Rightarrow$ "Explanation of PN generators using an example".
Question
Solution
(1) Correct is the proposed solution 2 ⇒ $G(D) = D^5 + D^3 +1$.
- The generator polynomial $G(D)$ denotes the feedback coefficients used for modulo-2 addition.
- $D$ is a formal parameter indicating a delay by one clock.
- $D^3$ then indicates a delay of three measures.
(2) It is $g_0 = g_3 = g_5 = 1$.
- All other feedback coefficients are $0$. It follows that:
- $$(g_{\rm 5}\hspace{0.1cm}g_{\rm 4}\hspace{0.1cm}g_{\rm 3}\hspace{0.1cm}g_{\rm 2}\hspace{0.1cm}g_{\rm 1}\hspace{0.1cm}g_{\rm 0})=\rm (101001)_{bin}\hspace{0.15cm} \underline{=(51)_{oct}}.$$
(3) Since the generator polynomial $G(D)$ is primitive, one obtains an "M-sequence".
- Accordingly, the period is maximal:
- $$P_{\rm max} = 2^{L}-1 \hspace{0.15cm}\underline {= 31}.$$
- In the theory part, the table with PN generators of maximum length ("M-sequences") for degree $L=5$ lists the configuration $(51)_{\rm oct}$.
(4) The reciprocal polynomial is:
- $$G_{\rm R}(D)=D^{\rm 5}\cdot(D^{\rm -5}+\D^{\rm -3}+ 1)= D^{\rm 5}+D^{\rm 2}+1.$$
- Thus, the octal identifier für this configuration: $\rm (100101)_{bin}\hspace{0.15cm} \underline{=(45)_{oct}}.$
(5) The solutions 1, 3, and 4 are correct:
- The output sequence of the reciprocal realization $G_{\rm R}(D)$ of a primitive polynomial $G(D)$ is also an "M-sequence".
- Both sequences are inverses of each other. This means:
- The output sequence of $(45)_{\rm oct}$ is equal to the output sequence of $(51)_{\rm oct}$ when read from right to left, additionally taking into account a phase ("cyclic shift").
- The prerequisite is again that not all memory cells are preallocated with zeros.
- Under this condition, both sequences actually have the same statistical properties.