Difference between revisions of "Theory of Stochastic Signals/Two-Dimensional Gaussian Random Variables"
m (Text replacement - "„" to """) |
|||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Random Variables with Statistical Dependence |
| − | |Vorherige Seite= | + | |Vorherige Seite=Two-Dimensional Random Variables |
| − | |Nächste Seite= | + | |Nächste Seite=Linear Combinations of Random Variables |
}} | }} | ||
| − | == | + | ==PDF and CDF== |
<br> | <br> | ||
| − | + | All previous statements of the fourth main chapter "Random Variables with Statistical Dependence" apply in general. | |
| − | + | For the special case '''Gaussian random variables'''' - the name goes back to the scientist [https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss Carl Friedrich Gauss] - we can further note: | |
| − | * | + | *The composite probability density function of a Gaussian 2D random variable $(x, y)$ with mean values $m_x = 0$, $m_y = 0$ and correlation coefficients $ρ_{xy}$ is: |
| − | :$$f_{xy}(x,y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_x \cdot \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$$ | + | : $$f_{xy}(x, y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_x \cdot \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1- \it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$$ |
| − | * | + | *Replacing $x$ by $(x - m_x)$ and $y$ by $(y- m_y)$, we obtain the more general PDF of a two-dimensional Gaussian random variable with mean. |
| − | * | + | *The two marginal probability density functions $f_{x}(x)$ and $f_{y}(y)$ of a 2D Gaussian random variable are also Gaussian with rms $σ_x$ and $σ_y$, respectively. |
| − | * | + | *For uncorrelated components $x$ and $y$ in the above equation $ρ_{xy} = 0$ must be substituted, and then the result is obtained: |
| − | :$$f_{xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it | + | :$$f_{xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it f_{x} \rm ( \it x \rm ) \cdot \it f_{y} \rm ( \it y \rm ) .$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ In the special case of a 2D random variable with Gaussian PDF $f_{xy}(x, y)$ ''uncorrelatedness'' also directly follows ''statistical independence:'' |
:$$f_{xy}(x,y)= f_{x}(x) \cdot f_{y}(y) . $$ | :$$f_{xy}(x,y)= f_{x}(x) \cdot f_{y}(y) . $$ | ||
| − | + | Please note: | |
| − | * | + | *In no other PDF can ''uncorrelatedness'' be used to infer ''statistical independence'' . |
| − | * | + | *However, one can always ⇒ infer ''uncorrelatedness'' from ''statistical independence'' for any 2D PDF $f_{xy}(x, y)$ because: |
| − | * | + | *If two random variables $x$ and $y$ are completely (statistically) independent of each other, then of course there are no ''linear'' dependencies between them <br>⇒ they are then also uncorrelated. }} |
| − | [[File:EN_Sto_T_4_2_S1.png |right|frame| | + | [[File:EN_Sto_T_4_2_S1.png |right|frame| 2D Gaussian PDF and 2D CDF]] |
| − | {{GraueBox|TEXT= | + | {{GraueBox|TEXT= |
| − | $\text{ | + | $\text{Example 1:}$ The two graphs show. |
| − | * | + | *the probability density function (left) and |
| − | * | + | *distribution function (right) |
| − | + | of a two-dimensional Gaussian random variable $(x, y)$ with relatively strong positive correlation of the individual components: $ρ_{xy} = 0.8$. | |
| − | + | As in the previous examples, the 2D random variable is more extended in $x$ direction than in $y$ direction: $σ_x = 2 - σ_y$. | |
<br clear=all> | <br clear=all> | ||
| − | + | These representations can be interpreted as follows: | |
| − | * | + | *The PDF here is comparable to a mountain ridge extending from the lower left to the upper right. |
| − | * | + | *The maximum is at $m_x = 0$ and $m_y = 0$. This means that the the 2D random variable is mean-free. |
| − | * | + | *The 2D CDF as the integral in two directions over the 2D PDF increases continuously from lower left to upper right from $0$ to $1$ . }} |
| − | + | The interactive applet [[Applets:Two-dimensional_Gaussian_Random_Variables|PDF and CDF for 2D Gaussian random variables]] allows plotting the two-dimensional functions for arbitrary values of $σ_x, \ σ_y$ and $ρ_{xy}$. | |
| − | |||
==Höhenlinien bei unkorrelierten Zufallsgrößen== | ==Höhenlinien bei unkorrelierten Zufallsgrößen== | ||
Revision as of 17:31, 23 January 2022
Contents
PDF and CDF
All previous statements of the fourth main chapter "Random Variables with Statistical Dependence" apply in general.
For the special case Gaussian random variables' - the name goes back to the scientist Carl Friedrich Gauss - we can further note:
- The composite probability density function of a Gaussian 2D random variable $(x, y)$ with mean values $m_x = 0$, $m_y = 0$ and correlation coefficients $ρ_{xy}$ is:
- $$f_{xy}(x, y)=\frac{\rm 1}{\rm 2\it\pi \cdot \sigma_x \cdot \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1- \it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$$
- Replacing $x$ by $(x - m_x)$ and $y$ by $(y- m_y)$, we obtain the more general PDF of a two-dimensional Gaussian random variable with mean.
- The two marginal probability density functions $f_{x}(x)$ and $f_{y}(y)$ of a 2D Gaussian random variable are also Gaussian with rms $σ_x$ and $σ_y$, respectively.
- For uncorrelated components $x$ and $y$ in the above equation $ρ_{xy} = 0$ must be substituted, and then the result is obtained:
- $$f_{xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}\hspace{-0.08cm}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it f_{x} \rm ( \it x \rm ) \cdot \it f_{y} \rm ( \it y \rm ) .$$
$\text{Conclusion:}$ In the special case of a 2D random variable with Gaussian PDF $f_{xy}(x, y)$ uncorrelatedness also directly follows statistical independence:
- $$f_{xy}(x,y)= f_{x}(x) \cdot f_{y}(y) . $$
Please note:
- In no other PDF can uncorrelatedness be used to infer statistical independence .
- However, one can always ⇒ infer uncorrelatedness from statistical independence for any 2D PDF $f_{xy}(x, y)$ because:
- If two random variables $x$ and $y$ are completely (statistically) independent of each other, then of course there are no linear dependencies between them
⇒ they are then also uncorrelated.
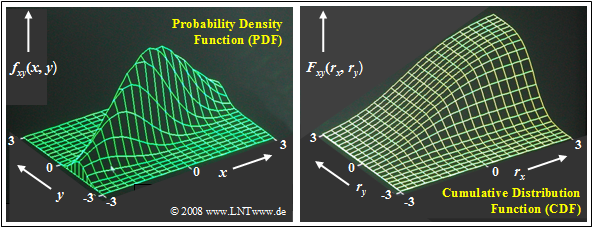
$\text{Example 1:}$ The two graphs show.
- the probability density function (left) and
- distribution function (right)
of a two-dimensional Gaussian random variable $(x, y)$ with relatively strong positive correlation of the individual components: $ρ_{xy} = 0.8$.
As in the previous examples, the 2D random variable is more extended in $x$ direction than in $y$ direction: $σ_x = 2 - σ_y$.
These representations can be interpreted as follows:
- The PDF here is comparable to a mountain ridge extending from the lower left to the upper right.
- The maximum is at $m_x = 0$ and $m_y = 0$. This means that the the 2D random variable is mean-free.
- The 2D CDF as the integral in two directions over the 2D PDF increases continuously from lower left to upper right from $0$ to $1$ .
The interactive applet PDF and CDF for 2D Gaussian random variables allows plotting the two-dimensional functions for arbitrary values of $σ_x, \ σ_y$ and $ρ_{xy}$.
Höhenlinien bei unkorrelierten Zufallsgrößen
Aus der Bedingungsgleichung $f_{xy}(x, y) = \rm const.$ können die Höhenlinien der WDF berechnet werden.
Sind die Komponenten $x$ und $y$ unkorreliert $(ρ_{xy} = 0)$, so erhält man als Gleichung für die Höhenlinien:
- $$\frac{x^{\rm 2}}{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{y}^{\rm 2}} =\rm const.$$
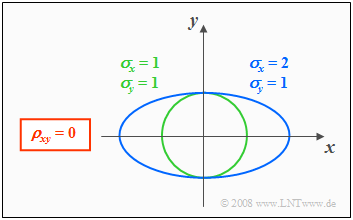
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:
- Kreise $($falls $σ_x = σ_y$, grüne Kurve$)$, oder
- Ellipsen $($für $σ_x ≠ σ_y$, blaue Kurve$)$ in Ausrichtung der beiden Achsen.
$\text{Beispiel 2:}$
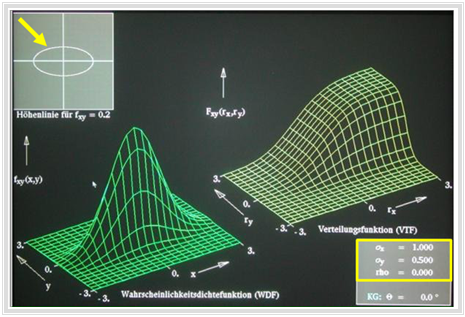
- Weitere Informationen zu dieser Thematik mit Signalbeispielen bietet der erste Teil "Gaußsche Zufallsgrößen ohne statistische Bindungen" des Lernvideos
- Die Grafik zeigt eine Momentaufnahme dieses Lernvideos.
- Der zweite Teil behandelt "Gaußsche Zufallsgrößen mit statistischen Bindungen" gemäß dem folgenden Abschnitt.
Höhenlinien bei korrelierten Zufallsgrößen
Bei korrelierten Komponenten $(ρ_{xy} ≠ 0)$ sind die Höhenlinien der WDF stets elliptisch, also auch für den Sonderfall $σ_x = σ_y$.
Hier lautet die Bestimmungsgleichung der WDF-Höhenlinien:
- $$f_{xy}(x, y) = {\rm const.} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \frac{x^{\rm 2} }{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2} }{\sigma_{y}^{\rm 2} }-{\rm 2}\cdot\rho_{xy}\cdot\frac{x\cdot y}{\sigma_x\cdot \sigma_y}={\rm const.}$$
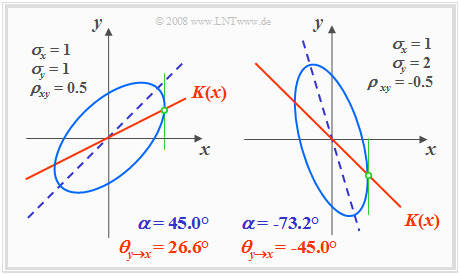
Die folgende Grafik zeigt in hellerem Blau zwei Höhenlinien für unterschiedliche Parametersätze, jeweils mit $ρ_{xy} ≠ 0$.
- Die Ellipsenhauptachse ist dunkelblau gestrichelt.
- Die Korrelationsgerade $K(x)$ ist durchgehend rot eingezeichnet.
Anhand dieser Darstellung sind folgende Aussagen möglich:
- Die Ellipsenform hängt außer vom Korrelationskoeffizienten $ρ_{xy}$ auch vom Verhältnis der beiden Streuungen $σ_x$ und $σ_y$ ab.
- Der Neigungswinkel $α$ der Ellipsenhauptachse (gestrichelte Gerade) gegenüber der $x$–Achse hängt ebenfalls von $σ_x$, $σ_y$ und $ρ_{xy}$ ab:
- $$\alpha = {1}/{2} \cdot {\rm arctan } \ ( 2 \cdot \rho_{xy} \cdot \frac {\sigma_x \cdot \sigma_y}{\sigma_x^2 - \sigma_y^2}).$$
- Die (rote) Korrelationsgerade $y = K(x)$ einer Gaußschen 2D–Zufallsgröße liegt stets unterhalb der (blau gestrichelten) Ellipsenhauptachse.
- $K(x)$ kann auch aus dem Schnittpunkt der Höhenlinien und ihrer vertikalen Tangenten geometrisch konstruiert werden, wie es in obigen Skizzen in grüner Farbe angedeutet ist.
Weitere Informationen zu dieser Thematik liefert das Lernvideo Gaußsche 2D-Zufallsgrößen:
- Teil 1: Gaußsche Zufallsgrößen ohne statistische Bindungen,
- Teil 2: Gaußsche Zufallsgrößen mit statistischen Bindungen.
Drehung des Koordinatensystems
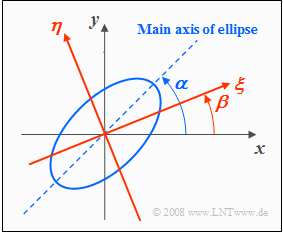
Bei manchen Aufgabenstellungen ist es vorteilhaft, das Koordinatensystem zu drehen, wie in der folgenden Grafik angedeutet:
- Das $(ξ, η)$-Koordinatensystem ist gegenüber dem ursprünglichen $(x, y)$-System um den Winkel $β$ gedreht.
- Dagegen bezeichnet $α$ den Winkel zwischen der Ellipsenhauptachse und der $x$–Achse.
Zwischen den Koordinaten der beiden Bezugssysteme bestehen folgende Zusammenhänge:
- $$\xi = \hspace{0.4cm} \cos (\beta) \cdot x + \sin (\beta) \cdot y \hspace{0.55cm}{\rm bzw. }\hspace{0.5cm} x = \cos (\beta) \cdot \xi - \sin (\beta) \cdot \eta ,$$
- $$\eta = - \sin (\beta) \cdot x + \cos (\beta) \cdot y \hspace{0.5cm}{\rm bzw. }\hspace{0.5cm} y = \sin (\beta) \cdot \xi + \cos (\beta) \cdot \eta .$$
Ist $(x, y)$ eine Gaußsche 2D-Zufallsgröße, so ist die Zufallsgröße $(ξ, η)$ ebenfalls gaußverteilt.
Setzt man die obigen Gleichungen in die 2D-WDF $f_{xy}(x, y)$ ein und vergleicht die Koeffizienten, so erhält man folgende Bestimmungsgleichungen für $σ_x$, $σ_y$ und $ρ_{xy}$ bzw. für $σ_ξ, σ_η$ und $ρ_{ξη}$:
- $$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\cos^2 (\beta)}{\sigma_{x}^2 } + \frac {\sin^2 (\beta)}{\sigma_{y}^2 } - 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$$
- $$\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin^2 (\beta)}{\sigma_{x}^2 } + \frac {\cos^2 (\beta)}{\sigma_{y}^2 } + 2 \rho_{xy} \cdot \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x} \cdot \sigma_{y}}\right ] ,$$
- $$\frac {\rho_{\xi \eta}}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \frac {1}{(1 - \rho_{xy}^2) } \left[ \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{x}^2 } - \frac {\sin (\beta) \cdot \cos (\beta)}{\sigma_{y}^2 } + \frac {\rho_{xy}}{\sigma_{x} \cdot \sigma_{y}} \cdot ( \cos^2( \beta) -\sin^2( \beta)) \right ] .$$
Mit diesen drei Gleichungen können die jeweils drei Parameter der beiden Koordinatensysteme direkt umgerechnet werden, was allerdings nur in Sonderfällen ohne erheblichen Rechenaufwand möglich ist. Es folgt ein Beispiel mit vertretbarem Rechenaufwand.
$\text{Beispiel 3:}$ Wir betrachten eine Gaußsche 2D-WDF mit folgenden Eigenschaften:
- Die Varianzen der beiden Komponenten sind gleich: $σ_x^2 = σ_y^2 = 1$.
- Der Korrelationskoeffizient zwischen $x$ und $y$ ist $ρ_{xy} = 0.5$.
- Der Winkel der Ellipsenhauptachse gegenüber der $x$–Achse beträgt somit $α = 45^\circ$.
Würde man das Koordinatensystem ebenfalls um $β =45^\circ$ drehen, so ergäbe sich wegen $σ_x = σ_y$ und wegen $\sin(β) = \cos(β) = 1/\sqrt{2}$ für den neuen Korrelationskoeffizienten $ρ_{ξη} = 0$ ⇒ unkorrelierte Komponenten.
Die beiden Streuungen – bezogen auf das neue Koordinatensystem – ergäben sich dann entsprechend den beiden ersten Gleichungen zu $σ_ξ = \sqrt{1.5}$ und $σ_η = \sqrt{0.5}$.
Der obigen Skizze ist allerdings nicht $β = α$ zugrundegelegt, sondern $β = α/2$.
- Mit $σ_x = σ_y = 1$, $ρ_{xy} = 0.5$,
- sowie $α = 45^\circ$, $\sin(β) · \cos(β) = \sin(2β)/2 = \sin(α)/2$ und
- $\cos^2(β) - \sin^2(β) = \cos(2β)= \cos(α)$
kann das Gleichungssystem wie folgt dargestellt werden:
- $${\rm (I)}\hspace{0.8cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2} = \frac {4}{3} \left[ 1 - \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 0.862 ,$$
- $${\rm (II)}\hspace{0.68cm}\frac {1}{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\eta^2} = \frac {4}{3} \left[ 1 + \frac {1}{2}\cdot {\sin (\alpha) }\right ] = 1.805 ,\hspace{0.28cm}\frac {\rm (I)}{\rm (II)}: \frac {\sigma_\eta}{\sigma_\xi} = \sqrt{\frac{0.862}{1.805} }= 0.691,$$
- $${\rm (III)}\hspace{0.54cm}\frac {\rho_{\xi \eta} }{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi\cdot \sigma_\eta}= \frac {\rho_{\xi \eta} }{(1 - \rho_{\xi \eta}^2) \cdot \sigma_\xi^2 \cdot 0.691}=\frac {2}{3}\cdot \cos( \alpha) = 0.471.$$
Dividiert man nun die Gleichung $\rm (III)$ durch die Gleichung $\rm (I)$, so erhält man:
- $$ \frac {\rho_{\xi \eta} }{0.691}=\frac {0.471}{0.862}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rho_{\xi \eta} }= 0.378.$$
Die beiden weiteren Parameter des neuen Koordinatensystems ergeben sich nun zu $σ_ξ ≈ 1$ und $σ_η ≈ 0.7$.
Aufgaben zum Kapitel
Aufgabe 4.4Z: Höhenlinien der 2D-WDF
Aufgabe 4.5: 2D-Prüfungsauswertung
Aufgabe 4.6: Koordinatendrehung