Difference between revisions of "Aufgaben:Exercise 5.9: Selection of OFDM Parameters"
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/OFDM_for_4G_Networks |
}} | }} | ||
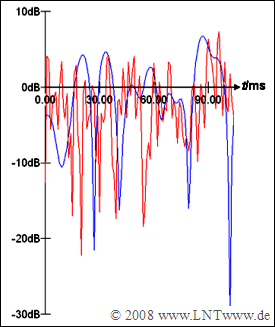
| − | [[File:P_ID1668__Mod_A_5_9.png|right|frame| | + | [[File:P_ID1668__Mod_A_5_9.png|right|frame|Time-dependent attenuation curve |
| − | In | + | of two mobile radio channels]] |
| − | + | In this exercise, some OFDM parameters of a mobile radio system are to be determined. | |
| − | |||
| − | |||
| − | |||
| + | The following assumptions are made: | ||
| + | * The coherence time of the channel is $T_{\rm coh} = 0.4 \ \rm ms$. | ||
| + | * The maximum path delay is $τ_{\rm max} = 25 \ \rm µ s$. | ||
| + | * The data rate (bit rate) is $R_{\rm B} = 1 \ \rm Mbit/s$. | ||
| + | * All subcarriers are $\rm 4–QAM$ modulated. | ||
| − | + | ||
| + | To ensure some robustness of the system to time and frequency selective fading, the following inequality must be satisfied: | ||
:$$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$ | :$$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$ | ||
| − | + | Overall, the following procedure should be followed: | |
| − | * | + | * Preliminary determination of the guard interval duration $(T_{\rm G}')$, |
| − | * | + | * Determination of the optimal core symbol duration $(T)$, |
| − | * | + | * corresponding determination of the number of sampling points of the $\rm FFT$. |
| + | |||
| + | |||
| + | After that, it may be necessary to redetermine some system quantities due to the rounding performed during the calculations. | ||
| − | + | The diagram shows two exemplary attenuation curves of mobile radio systems in logarithmic representation. | |
| + | *In the case of the blue curve, the changes over time occur relatively slowly, while in the case of the red curve they occur four times as fast. | ||
| + | *Consequently, the blue channel has a four times larger coherence time than the red channel. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | Notes: |
| + | *The exercise belongs to the chapter [[Modulation_Methods/OFDM_für_4G–Netze|OFDM for 4G Networks]]. | ||
| + | *Reference is made in particular to the section [[Modulation_Methods/OFDM_for_4G_Networks#Determination_of_some_OFDM_parameters|Determination of some OFDM parameters]]. | ||
| + | * Further information on the topic can be found in the LNTwww book [[Mobile Communications]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the minimum reasonable duration $T_{\rm G}'$ of the "preliminary guard interval". |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm G}' \ = \ $ { 25 3% } $\ \rm | + | $T_{\rm G}' \ = \ $ { 25 3% } $\ \rm µ s$ |
| − | { | + | {Determine the optimal core symbol duration $T_{\rm opt}$ as a geometric mean. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm opt} \ = \ $ { 97 3% } $\ \rm | + | $T_{\rm opt} \ = \ $ { 97 3% } $\ \rm µ s$ |
| − | { | + | {Determine the required number of useful carriers. |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm user} \ = \ $ { 61 1% } |
| − | { | + | {Specify the resulting number of interpolation points of the FFT. |
|type="{}"} | |type="{}"} | ||
$N_{\rm FFT} \ = \ $ { 64 1% } | $N_{\rm FFT} \ = \ $ { 64 1% } | ||
| − | { | + | {Calculate the number $N_{\rm G}$ of time samples of the guard interval and from this the new resulting guard duration $T_{\rm G}$. |
|type="{}"} | |type="{}"} | ||
$N_{\rm G} \ = \ $ { 17 1% } | $N_{\rm G} \ = \ $ { 17 1% } | ||
| − | $T_{\rm G} \ = \ $ { 26 1% } $\ \rm | + | $T_{\rm G} \ = \ $ { 26 1% } $\ \rm µ s$ |
| − | { | + | {Now use your calculations to specify the duration $T_{\rm R}$ of a frame. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm R} \ = \ $ { 123 1% } $\ \rm | + | $T_{\rm R} \ = \ $ { 123 1% } $\ \rm µ s$ |
| − | { | + | {What is the total number of samples contained in a frame? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm total} \ = \ $ { 81 1% } |
| − | { | + | {Using the determined parameters, determine the number of useful carriers $N_{\rm use}'$ again. |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm user}' \ = \ $ { 62 1% } |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' It holds that $T_{\rm G}' = \tau_{\rm max} \hspace{0.15cm}\underline { = 25\ \rm µ s}$. |
| + | *This establishes the lower limit of the inequality $T_{\rm{G}}' \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}'$. | ||
| + | *However, the upper limit can now also be calculated since the coherence time $T_{\rm coh} = 400\ \rm µ s$ is known. | ||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(2)''' The geometric mean is used to reasonably solve the inequality from '''(1)''': |
| − | :$$N_{{\rm{ | + | :$$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm µ s}} \cdot ({400\,\,{\rm µ s}} - {25\,\,{\rm µ s}})} \hspace{0.15cm}\underline { \approx {97\,\,{\rm µ s}}}.$$ |
| − | = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm | + | |
| + | |||
| + | '''(3)''' The required number of useful carriers is given by the following equation: | ||
| + | :$$N_{{\rm{user}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil | ||
| + | = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {25\,\,{\rm µ s}} )} | ||
{{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$ | {{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$ | ||
| − | '''(4)''' | + | |
| + | '''(4)''' The number of interpolation points of the $\rm FFT$ must always be a power of two. It follows that: | ||
:$$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$ | :$$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$ | ||
| − | + | *Unused carriers can be used as guard bands at the edges of the spectrum. | |
| + | |||
| + | |||
| + | '''(5)''' We denote the rounded number of grid points of the guard interval by $N_{\rm{G}}$. Then holds: | ||
| + | :$$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm µ s}} {97\,\,{\rm µ s}} \cdot 64 } \right\rceil \hspace{0.15cm}\underline {= 17},$$ | ||
| + | :$$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm µ s}}} {64}\hspace{0.15cm}\underline { \approx {26\,\,{\rm µ s}}}.$$ | ||
| + | |||
| + | '''(6)''' The frame duration results to | ||
| + | :$$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm µ s}} + {26\,\,{\rm µ s}}\hspace{0.15cm}\underline {= {123\,\,{\rm µ s}}}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(7)''' Using the results of subtasks '''(4)''' and '''(5)''', we obtain: |
| − | :$$ | + | :$$ N_{\rm{total}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$ |
| − | |||
| − | |||
| − | '''(8)''' | + | '''(8)''' The recalculation is necessary because the duration of the guard interval may have changed. |
| − | :$$N_ | + | *Compared to subtask '''(3)''', the provisional length $T_{\rm{G}} '$ is replaced by $T_{\rm{G}} $ and a slightly different result is obtained: |
| − | + | :$$N_{\rm user}' = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {26\,\,{\rm µ s}} )} {{{\rm{log_2}}(4)}}}\right\rceil = \left\lceil 61.5\right\rceil\hspace{0.15cm}\underline {= 62}.$$ | |
| + | *However, this still gives $N_{\rm FFT} = 64$. | ||
| Line 110: | Line 128: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^5.7 OFDM for 4G Networks^]] |
Latest revision as of 12:13, 25 January 2022
In this exercise, some OFDM parameters of a mobile radio system are to be determined.
The following assumptions are made:
- The coherence time of the channel is $T_{\rm coh} = 0.4 \ \rm ms$.
- The maximum path delay is $τ_{\rm max} = 25 \ \rm µ s$.
- The data rate (bit rate) is $R_{\rm B} = 1 \ \rm Mbit/s$.
- All subcarriers are $\rm 4–QAM$ modulated.
To ensure some robustness of the system to time and frequency selective fading, the following inequality must be satisfied:
- $$T_{\rm{G}} \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}.$$
Overall, the following procedure should be followed:
- Preliminary determination of the guard interval duration $(T_{\rm G}')$,
- Determination of the optimal core symbol duration $(T)$,
- corresponding determination of the number of sampling points of the $\rm FFT$.
After that, it may be necessary to redetermine some system quantities due to the rounding performed during the calculations.
The diagram shows two exemplary attenuation curves of mobile radio systems in logarithmic representation.
- In the case of the blue curve, the changes over time occur relatively slowly, while in the case of the red curve they occur four times as fast.
- Consequently, the blue channel has a four times larger coherence time than the red channel.
Notes:
- The exercise belongs to the chapter OFDM for 4G Networks.
- Reference is made in particular to the section Determination of some OFDM parameters.
- Further information on the topic can be found in the LNTwww book Mobile Communications.
Questions
Solution
- This establishes the lower limit of the inequality $T_{\rm{G}}' \ll T \ll T_{{\rm{coh}}} - T_{\rm{G}}'$.
- However, the upper limit can now also be calculated since the coherence time $T_{\rm coh} = 400\ \rm µ s$ is known.
(2) The geometric mean is used to reasonably solve the inequality from (1):
- $$T_{{\rm{opt}}} = \sqrt {T_{\rm{G}} ' \cdot (T_{{\rm{coh}}} - T_{\rm{G}} ')} = \sqrt {{25\,\,{\rm µ s}} \cdot ({400\,\,{\rm µ s}} - {25\,\,{\rm µ s}})} \hspace{0.15cm}\underline { \approx {97\,\,{\rm µ s}}}.$$
(3) The required number of useful carriers is given by the following equation:
- $$N_{{\rm{user}}} = \left\lceil {\frac{{R_{{\rm{B}}} \cdot (T + T_{\rm{G}} ')}} {{{\rm{log}_2}(M)}}}\right\rceil = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {25\,\,{\rm µ s}} )} {{{\rm{log}_2}(4)}}}\right\rceil\hspace{0.15cm}\underline {= 61}.$$
(4) The number of interpolation points of the $\rm FFT$ must always be a power of two. It follows that:
- $$ N_{{\rm{FFT}}} = 2^{\left\lceil {{\rm{log_2}} \hspace{0.05cm}(61 )} \right\rceil } = 2^6\hspace{0.15cm}\underline {= 64}.$$
- Unused carriers can be used as guard bands at the edges of the spectrum.
(5) We denote the rounded number of grid points of the guard interval by $N_{\rm{G}}$. Then holds:
- $$N_{\rm{G}} = \left\lceil {\frac{{T_{\rm{G}} '}} {{T_{{\rm{opt}}} }} \cdot N_{{\rm{FFT}}} } \right\rceil = \left\lceil {\frac{25\,\,{\rm µ s}} {97\,\,{\rm µ s}} \cdot 64 } \right\rceil \hspace{0.15cm}\underline {= 17},$$
- $$ T_{\rm{G}} = N_{\rm{G}} \cdot \frac{{T_{{\rm{opt}}} }} {{N_{{\rm{FFT}}} }}= 17 \cdot \frac{{97\,\,{\rm µ s}}} {64}\hspace{0.15cm}\underline { \approx {26\,\,{\rm µ s}}}.$$
(6) The frame duration results to
- $$T_{\rm{R}} = T + T_{\rm{G}} = {97\,\,{\rm µ s}} + {26\,\,{\rm µ s}}\hspace{0.15cm}\underline {= {123\,\,{\rm µ s}}}.$$
(7) Using the results of subtasks (4) and (5), we obtain:
- $$ N_{\rm{total}} = N_{\rm{FFT}} + N_{\rm{G}} = 64 + 17 \hspace{0.15cm}\underline {= 81}.$$
(8) The recalculation is necessary because the duration of the guard interval may have changed.
- Compared to subtask (3), the provisional length $T_{\rm{G}} '$ is replaced by $T_{\rm{G}} $ and a slightly different result is obtained:
- $$N_{\rm user}' = \left\lceil {\frac{10^6\,\,{\rm bit/s} \cdot ({97\,\,{\rm µ s}} + {26\,\,{\rm µ s}} )} {{{\rm{log_2}}(4)}}}\right\rceil = \left\lceil 61.5\right\rceil\hspace{0.15cm}\underline {= 62}.$$
- However, this still gives $N_{\rm FFT} = 64$.