Aufgaben:Exercise 1.5: Cosine-Square Spectrum

• Return to book

Cosinus-Quadrat-Nyquistspektrum

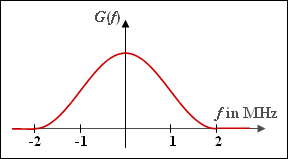
Betrachtet wird das Spektrum  $G(f)$  mit  $\cos^{2}$–förmigem Verlauf entsprechend der Skizze. Dieses erfüllt das erste Nyquistkriterium:

$$\sum_{k = -\infty}^{+\infty} G(f -{k}/{T} ) = {\rm const.}$$

Dementsprechend hat der zugehörige Impuls  $g(t)$  Nulldurchgänge bei Vielfachen von  $T$, wobei  $T$  noch zu bestimmen ist. Durch Fourierrücktransformation von  $G(f)$  erhält man die Gleichung für den Zeitverlauf:

$$g( t )= g_0 \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\cdot {\rm si}(\pi \cdot {t}/{T})\hspace{0.05cm}.$$

In den Fragen zu dieser Aufgabe werden auf folgende Eigenschaften Bezug genommen:

• Die Spektralfunktion  $G(f)$  ist ein Sonderfall des Cosinus–Rolloff–Spektrums, das punktsymmetrisch um die Nyquistfrequenz  $f_{\rm Nyq}$  ist.
• Das Cosinus–Rolloff–Spektrum ist durch die Eckfrequenzen  $f_{1}$  und  $f_{2}$  vollständig gekennzeichnet.
• Für  $| f | < f_{1}$  ist  $G(f) = g_{0} \cdot T = \rm const.$, während das Spektrum für  $| f | > f_{2}$  keine Anteile besitzt.
• Der Zusammenhang zwischen der Nyquistfrequenz und den Eckfrequenzen lautet:

$$f_{\rm Nyq}= \frac{f_1 +f_2 } {2 }\hspace{0.05cm}.$$

• Die Flankensteilheit wird durch den so genannten Rolloff–Faktor charakterisiert:

$$r = \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.2cm}(0 \le r \le 1) \hspace{0.05cm}.$$

Hinweis:

• Die Aufgabe gehört zum Kapitel  Eigenschaften von Nyquistsystemen.

Fragebogen

1

Welche Eckfrequenzen besitzt dieses Cosinus–Rolloff–Spektrum?

$f_{1} \ = \ $ $\ \rm MHz$

$f_{2} \ = \ $ $\ \rm MHz$

2

Wie groß sind die Nyquistfrequenz und der Rolloff–Faktor?

$f_{\rm Nyq} \ = \ $ $\ \rm MHz$

$r \ = \ $

3

In welchem zeitlichen Abstand  $T$  besitzt  $g(t)$  Nulldurchgänge?

$T \ = \ $ $\ \rm µ s$

4

Welche der folgenden Aussagen sind zutreffend?

	$g(t)$  erfüllt das erste Nyquistkriterium wegen des  $\rm si$–Terms.
	$g(t)$  besitzt weitere Nulldurchgänge bei  $\pm 0.5T,  \pm 1.5T,  \pm 2.5 T, \text{...}$
	Das  $\cos^{2}$–Spektrum erfüllt auch das zweite Nyquistkriterium.

5

Welchen (normierten) Wert besitzt der Impuls zum Zeitpunkt  $t = T/2$?

$g(t = T/2)/g_{0} \ = \ $

Musterlösung

Solution

(1)  Die obere Eckfrequenz kann aus der Grafik abgelesen werden:   $f_{2} \underline{= 2 \ \rm MHz}$. Da das Spektrum in keinem Bereich konstant ist, gilt $f_{1} \underline {= 0}$.

(2)  Aus den angegebenen Gleichungen erhält man:

$$f_{\rm Nyq} = \ \frac{f_1 +f_2 } {2 }\hspace{0.1cm}\underline { = 1\,{\rm MHz}}\hspace{0.05cm},\hspace{0.5cm} r = \ \frac{f_2 -f_1 } {f_2 +f_1 }\hspace{0.1cm}\underline { = 1 }\hspace{0.05cm}.$$

(3)  Der Abstand äquidistanter Nulldurchgänge hängt direkt mit der Nyquistfrequenz zusammen:

$$f_{\rm Nyq}= \frac{1}{2T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} T= \frac{1}{2f_{\rm Nyq}}\hspace{0.1cm}\underline { = 0.5\,{\rm µ s}}\hspace{0.05cm}.$$

(4)  Richtig sind die Aussagen 1 und 3:

• Die erste Aussage ist richtig:   Die Funktion $si(π · t/T)$ führt zu Nulldurchgängen bei $\nu T (\nu \neq 0)$.
• Auch die letzte Aussage trifft zu:  Wegen $g(t) = 0$ für $t =\pm 1.5T, \pm 2.5T, \pm 3.5T, ...$ wird auch das zweite Nyquistkriterium erfüllt.
• Falsch ist dagegen die mittlere Aussage, da $g(t = T/2) \neq 0$ ist.

• Die Bedingung für das zweite Nyquistkriterium lautet im Frequenzbereich:

$$G_{\rm Per}(f) = \sum_{k = -\infty}^{+\infty} \frac {G \left ( f - \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$$

• Die Bedingung ist beim cos$^{2}$–Spektrum tatsächlich erfüllt, wie man nach längerer Rechnung zeigen kann. Wir beschränken uns hier auf den Frequenzbereich $| f · T | \leq 1$ und setzen vereinfachend $g_{0} \cdot T = 1$:

$$G_{\rm Per}(f) = \frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]}+\frac {\cos^2 \left [\pi/2 \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\hspace{0.05cm}.$$

• Weiter gilt:

$$\frac {\cos^2 (x)}{\cos(2x)} = {1}/{2} \cdot \frac {1+\cos(2x)}{\cos(2x)}= {1}/{2} \cdot \left [1+ \frac {1}{\cos(2x)}\right ]$$

$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = {1}/{2} \cdot \left [1+ \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} - f) \cdot T \right ]} +1- \frac {1}{\cos \left [\pi \cdot ( f_{\rm Nyq} + f) \cdot T \right ]}\right ]\hspace{0.05cm}.$$

• Wegen $\cos \left [ \pi \cdot ( f_{\rm Nyq} \pm f) \cdot T \right] = \cos \left ( {\pi}/{2} \pm \pi f T \right) = \sin \left ( \pm \pi f T \right)\text{:}$

$$\Rightarrow \hspace{0.3cm} G_{\rm Per}(f) = 2 - \frac {1}{\sin (\pi f T)} + \frac {1}{\sin (\pi f T)} = 2 = {\rm const}\hspace{0.05cm}.$$

(5)  Für $t = T/2$ liefert die angegebene Gleichung einen unbestimmten Wert (0 geteilt durch 0), der mit der Regel von l'Hospital ermittelt werden kann.

• Dazu bildet man die Ableitungen von Zähler und Nenner und setzt in das Ergebnis den gewünschten Zeitpunkt $t = T/2$ ein:

$$\frac{g( t = T/2)}{g_0} = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{{\rm d}/{\rm d}t \left [ \cos(\pi \cdot t/T)\right]}{{\rm d}/{\rm d}t\left [ 1 - (2 \cdot t/T)^2\right]}} \bigg |_{t = T/2} = \ {{\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac{- \pi/T \cdot \sin(\pi \cdot t/T)}{-2 \cdot (2\cdot t/T) \cdot (2/T)}} \bigg |_{t = T/2} = \frac {2}{\pi}\cdot \frac {\pi}{4}\hspace{0.1cm}\underline { = 0.5}\hspace{0.05cm}.$$

• Ein zweiter Lösungsweg führt zu der Darstellung:

$$\frac{g( t )}{g_0} = {\rm si}(\pi \cdot \frac{t}{T}) \cdot \frac {\pi}{4} \cdot \big [ {\rm si}(\pi \cdot (t/T + 1/2)) + {\rm si}(\pi \cdot (t/T - 1/2))\big] \hspace{0.05cm}.$$

• Der zweite Klammerausdruck kann wie folgt umgeformt werden:

$$\frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {\pi}{4} \cdot \left [ \frac {{\rm sin}(\pi \cdot t/T + \pi/2)}{\pi \cdot t/T + \pi/2} + \frac {{\rm sin}(\pi \cdot t/T - \pi/2)}{\pi \cdot t/T - \pi/2}\right] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \left [ \frac {1}{2 \cdot t/T + 1} - \frac {1}{ 2 \cdot t/T - 1}\right]$$

$$\Rightarrow \hspace{0.3cm} \frac {\pi}{4} \cdot \bigg [ \hspace{0.1cm}... \hspace{0.1cm} \bigg ] = \ \frac {1}{2} \cdot {\rm cos}(\pi \cdot t/T )\cdot \frac{1- 2 \cdot t/T + 1+ 2 \cdot t/T}{(1+ 2 \cdot t/T)(1- 2 \cdot t/T)}= \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$$

• Daraus folgt, dass beide Ausdrücke tatsächlich gleich sind. Für den Zeitpunkt $t = T/2$ gilt somit weiterhin:

$$\frac{g( t = T/2)}{g_0} = {\rm si}( \frac{\pi}{2}) \cdot \frac {\pi}{4} \cdot \left [ {\rm si}(\pi ) + {\rm si}(0)\right]= \frac {2}{\pi}\cdot \frac {\pi}{4} = 0.5 \hspace{0.05cm}.$$