Difference between revisions of "Aufgaben:Exercise 1.1Z: Non-redundant Binary Source"
m (Guenter moved page Exercise 1.1Z: Nonredundant Binary Source to Exercise 1.1Z: Non-redundant Binary Source) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System |
}} | }} | ||
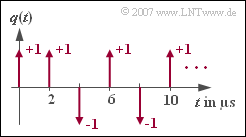
| − | [[File:P_ID1257__Dig_Z_1_1.png|right|frame| | + | [[File:P_ID1257__Dig_Z_1_1.png|right|frame|Dirac-shaped source signal]] |
| − | + | Any digital source can be completely described by its source symbol sequence | |
:$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | :$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | ||
| − | + | Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source. | |
| − | + | Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal | |
:$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$ | :$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$ | ||
| − | + | which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients. | |
| − | * | + | *In the case of a binary unipolar digital signal transmission, holds: |
:$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | :$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| − | * | + | *Correspondingly, in the case of a bipolar system: |
:$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | :$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| − | + | The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems. | |
| Line 24: | Line 24: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System|System Components of a Baseband Transmission System]]. |
| − | * | + | *Reference is made in particular to the section [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System#Descriptive_variables_of_the_digital_source|Descriptive variables of the digital source]]. |
| − | *In | + | *In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$. |
| − | * | + | *To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the symbol distance $T$? |
|type="{}"} | |type="{}"} | ||
$T \ = \ $ { 2 3% } $\ \rm µ s$ | $T \ = \ $ { 2 3% } $\ \rm µ s$ | ||
| − | { | + | {What is the bit rate $R$ output by the source? |
|type="{}"} | |type="{}"} | ||
$R \ = \ $ { 500 3% } $\ \rm kbit/s$ | $R \ = \ $ { 500 3% } $\ \rm kbit/s$ | ||
| − | { | + | {Is this representation unipolar or bipolar? |
|type="()"} | |type="()"} | ||
| − | - | + | - The symbol sequence is unipolar. |
| − | + | + | + The symbol sequence is bipolar. |
| − | { | + | {What is the source symbol $q_2$? |
|type="()"} | |type="()"} | ||
+ $q_2 = \rm L$, | + $q_2 = \rm L$, | ||
- $q_2 = \rm H$. | - $q_2 = \rm H$. | ||
| − | { | + | {What is the symbol probability $p_{\rm H} = {\rm Pr}(q_\nu = \rm H$)? |
|type="{}"} | |type="{}"} | ||
$p_{\rm H} \ = \ $ { 0.5 3% } | $p_{\rm H} \ = \ $ { 0.5 3% } | ||
| Line 59: | Line 59: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the diagram, the distance between two symbols is $\underline{T = 2\ \rm µ s}$. |
| − | '''(2)''' | + | '''(2)''' With this redundancy-free binary source – and only with such a source – the bit rate is $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$. |
| − | '''(3)''' | + | '''(3)''' The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is <u>bipolar</u>. |
| − | '''(4)''' | + | '''(4)''' The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. |
| − | * | + | *With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$. |
| − | '''(5)''' | + | '''(5)''' Even if the diagram suggests otherwise for the short time interval shown here: |
| − | * | + | *For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 17:37, 10 February 2022
Any digital source can be completely described by its source symbol sequence
- $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$
Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source.
Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal
- $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$
which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients.
- In the case of a binary unipolar digital signal transmission, holds:
- $$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
- Correspondingly, in the case of a bipolar system:
- $$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems.
Notes:
- The exercise belongs to the chapter System Components of a Baseband Transmission System.
- Reference is made in particular to the section Descriptive variables of the digital source.
- In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$.
- To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial.
Questions
Solution
(2) With this redundancy-free binary source – and only with such a source – the bit rate is $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$.
(3) The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is bipolar.
(4) The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$.
- With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$.
(5) Even if the diagram suggests otherwise for the short time interval shown here:
- For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold.