Difference between revisions of "Aufgaben:Exercise 5.4: Sine Wave Generator"
From LNTwww
| (21 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Digital_Filters |
}} | }} | ||
| − | [[File:P_ID622__Sto_A_5_4.png|right| | + | [[File:P_ID622__Sto_A_5_4.png|right|frame|Proposed filter structure]] |
| − | + | The diagram shows a second-order digital filter suitable for generating a discrete-time sinusoidal function on a digital signal processor $\rm (DSP)$, for example: | |
| − | :$$\left\langle {y_\nu } \right\rangle = \left\langle {\, \sin ( {\nu T | + | :$$\left\langle \hspace{0.05cm}{y_\nu }\hspace{0.05cm} \right\rangle = \left\langle {\, \sin ( {\nu T \cdot \omega _0 } )\, }\right\rangle .$$ |
| − | * | + | *It is assumed that the input sequence $\left\langle \hspace{0.05cm} {x_\nu } \hspace{0.05cm}\right\rangle$ describes a (discrete-time) Dirac delta function. Thus, all output values $y_\nu$ are simultaneously identical to zero for times $\nu\lt 0$. |
| − | * | + | *The total of five filter coefficients result from the [https://en.wikipedia.org/wiki/Z-transform $Z$-transform]: |
| − | :$$ | + | :$$Z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$ |
| − | * | + | *Substituting this equation by a recursive second order filter $(M = 2)$, we obtain the following filter coefficients: |
| − | :$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0,\ | + | :$$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0, \quad b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$ |
| − | + | In the diagram it is already marked by the lighter border that the filter coefficients $a_0$ and $a_2$ can be omitted. | |
| − | + | ||
| − | * | + | |
| − | * | + | |
| − | + | ||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Digital_Filters|Digital Filters]] in this book. | ||
| + | *The HTML5/JavaScript applet [[Applets:Digital_Filters|"Digital Filters"]] illustrates the subject matter of this chapter. | ||
| + | *For the subtasks '''(1)''' to '''(3)''' the following apply: | ||
:$$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$ | :$$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Let $a_1 = 0.5$ and $b_1 = \sqrt 3 $. Calculate the initial values $y_\nu$ at time points $\nu = 0$, $\nu = 1$ and $\nu = 2$. |
|type="{}"} | |type="{}"} | ||
| − | $y_0$ | + | $y_0 \ = \ $ { 0. } |
| − | $y_1$ | + | $y_1 \ = \ $ { 0.5 3% } |
| − | $y_2$ | + | $y_2 \ = \ $ { 0.866 3% } |
| − | { | + | {What is the initial value $y_\nu$ for $\nu \ge 2$ in general? Calculate the values $y_3$, ... , $y_7$ and enter $y_7$ as a check. |
|type="{}"} | |type="{}"} | ||
| − | $y_7$ | + | $y_7 \ = \ $ { -0.515--0.485 } |
| − | { | + | {How many grid points $(T_0/T)$ represent a period $(T_0)$? |
|type="{}"} | |type="{}"} | ||
| − | $T_0/T$ | + | $T_0/T\ = \ $ { 12 3% } |
| − | { | + | {Now $T = 1 \hspace{0.05cm} \rm µ s$ is valid. How must the coefficients $a_1$ and $b_1$ be selected so that a $\text{10 kHz}$ sine wave is generated? |
|type="{}"} | |type="{}"} | ||
| − | $a_1$ | + | $a_1 \ = \ $ { 0.062 3% } |
| − | $b_1$ | + | $b_1 \ = \ $ { 1.996 3% } |
| Line 50: | Line 54: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The "$1$" at the input affects $($because of $a_0= 0)$ at the output only at the time $\nu = 1$: | |
:$$y_0 \hspace{0.15cm} \underline{= 0},\quad y_1 \hspace{0.15cm} \underline{ = 0.5}.$$ | :$$y_0 \hspace{0.15cm} \underline{= 0},\quad y_1 \hspace{0.15cm} \underline{ = 0.5}.$$ | ||
| − | + | *At $\nu = 2$, the recursive part of the filter also takes effect: | |
:$$y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \hspace{0.15cm} \underline{ \approx 0.866}.$$ | :$$y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \hspace{0.15cm} \underline{ \approx 0.866}.$$ | ||
| − | + | ||
| + | |||
| + | '''(2)''' For $\nu \ge 2$, the filter is purely recursive: | ||
:$$y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2} .$$ | :$$y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2} .$$ | ||
| − | + | *In particular, one obtains | |
:$$y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1;$$ | :$$y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1;$$ | ||
:$$y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$$ | :$$y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$$ | ||
:$$y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = {1}/{2};$$ | :$$y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = {1}/{2};$$ | ||
:$$y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$$ | :$$y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$$ | ||
| − | :$$y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} \hspace{0.15cm} \underline{= - | + | :$$y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} \hspace{0.15cm} \underline{= - 0.5}.$$ |
| + | |||
| + | |||
| − | + | '''(3)''' By continuing the recursive algorithm of subtask '''(2)''', we obtain for large $\nu$–values: | |
:$$y_\nu = y_{\nu - 12} .$$ | :$$y_\nu = y_{\nu - 12} .$$ | ||
| + | *From this follows $T_0/T\hspace{0.15cm} \underline{= 12}$. The same result is obtained by the following considerations: | ||
| + | :$$a_1 = \sin \left( {\omega _0 \cdot T} \right) = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right)\mathop = \limits^! {1}/{2} = \sin \left( {{{\rm{\pi }}}/{6}} \right) \;\;{\rm \Rightarrow} \;\;{2T}/{T_0 } = {1}/{6}\quad \Rightarrow \;\;{T_0 }/{T} = 12.$$ | ||
| + | |||
| + | *Checking the coefficient $b_1$ confirms the calculation: | ||
| + | :$$b_1 = 2 \cdot \cos \left( {{{\rm{\pi }}}/{6}} \right) = 2 \cdot {\sqrt 3 }/{2} = \sqrt 3 .$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' From $f_0 = 10 \hspace{0.15cm} \rm kHz$ follows $T_0 = 100 \hspace{0.05cm} \rm µ s$ or $T_0/T = 100$ . This gives: | |
:$$a_1 = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = \sin \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 0.062},$$ | :$$a_1 = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = \sin \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 0.062},$$ | ||
:$$b_1 = 2 \cdot \cos \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = 2 \cdot \cos \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 1.996}.$$ | :$$b_1 = 2 \cdot \cos \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = 2 \cdot \cos \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 1.996}.$$ | ||
| Line 85: | Line 93: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^5.2 Digital Filters^]] |
Latest revision as of 18:53, 10 February 2022
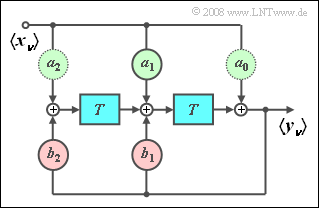
The diagram shows a second-order digital filter suitable for generating a discrete-time sinusoidal function on a digital signal processor $\rm (DSP)$, for example:
- $$\left\langle \hspace{0.05cm}{y_\nu }\hspace{0.05cm} \right\rangle = \left\langle {\, \sin ( {\nu T \cdot \omega _0 } )\, }\right\rangle .$$
- It is assumed that the input sequence $\left\langle \hspace{0.05cm} {x_\nu } \hspace{0.05cm}\right\rangle$ describes a (discrete-time) Dirac delta function. Thus, all output values $y_\nu$ are simultaneously identical to zero for times $\nu\lt 0$.
- The total of five filter coefficients result from the $Z$-transform:
- $$Z \{ {\sin ( {\nu T \omega _0 } )} \} = \frac{{z \cdot \sin \left( {\omega _0 T} \right)}}{{z^2 - 2 \cdot z \cdot \cos \left( {\omega _0 T} \right) + 1}}.$$
- Substituting this equation by a recursive second order filter $(M = 2)$, we obtain the following filter coefficients:
- $$a_0 = 0,\quad a_1 = \sin \left( {\omega _0 T} \right),\quad a_2 = 0, \quad b_1 = 2 \cdot \cos \left( {\omega _0 T} \right),\quad b_2 = - 1.$$
In the diagram it is already marked by the lighter border that the filter coefficients $a_0$ and $a_2$ can be omitted.
Notes:
- The exercise belongs to the chapter Digital Filters in this book.
- The HTML5/JavaScript applet "Digital Filters" illustrates the subject matter of this chapter.
- For the subtasks (1) to (3) the following apply:
- $$a_1 = 0.5,\quad b_1 = \sqrt 3 .$$
Questions
Solution
(1) The "$1$" at the input affects $($because of $a_0= 0)$ at the output only at the time $\nu = 1$:
- $$y_0 \hspace{0.15cm} \underline{= 0},\quad y_1 \hspace{0.15cm} \underline{ = 0.5}.$$
- At $\nu = 2$, the recursive part of the filter also takes effect:
- $$y_2 = b_1 \cdot y_1 - y_0 = {\sqrt 3 }/{2} \hspace{0.15cm} \underline{ \approx 0.866}.$$
(2) For $\nu \ge 2$, the filter is purely recursive:
- $$y_\nu = b_1 \cdot y_{\nu - 1} - y_{\nu - 2} .$$
- In particular, one obtains
- $$y_3 = \sqrt 3 \cdot y_2 - y_1 = \sqrt 3 \cdot {\sqrt 3 }/{2} - {1}/{2} = 1;$$
- $$y_4 = \sqrt 3 \cdot y_3 - y_2 = \sqrt 3 \cdot 1 - {\sqrt 3 }/{2} = {\sqrt 3 }/{2};$$
- $$y_5 = \sqrt 3 \cdot y_4 - y_3 = \sqrt 3 \cdot {\sqrt 3 }/{2} - 1 = {1}/{2};$$
- $$y_6 = \sqrt 3 \cdot y_5 - y_4 = \sqrt 3 \cdot {1}/{2} - {\sqrt 3 }/{2} = 0;$$
- $$y_7 = \sqrt 3 \cdot y_6 - y_5 = \sqrt 3 \cdot 0 - {1}/{2} \hspace{0.15cm} \underline{= - 0.5}.$$
(3) By continuing the recursive algorithm of subtask (2), we obtain for large $\nu$–values:
- $$y_\nu = y_{\nu - 12} .$$
- From this follows $T_0/T\hspace{0.15cm} \underline{= 12}$. The same result is obtained by the following considerations:
- $$a_1 = \sin \left( {\omega _0 \cdot T} \right) = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right)\mathop = \limits^! {1}/{2} = \sin \left( {{{\rm{\pi }}}/{6}} \right) \;\;{\rm \Rightarrow} \;\;{2T}/{T_0 } = {1}/{6}\quad \Rightarrow \;\;{T_0 }/{T} = 12.$$
- Checking the coefficient $b_1$ confirms the calculation:
- $$b_1 = 2 \cdot \cos \left( {{{\rm{\pi }}}/{6}} \right) = 2 \cdot {\sqrt 3 }/{2} = \sqrt 3 .$$
(4) From $f_0 = 10 \hspace{0.15cm} \rm kHz$ follows $T_0 = 100 \hspace{0.05cm} \rm µ s$ or $T_0/T = 100$ . This gives:
- $$a_1 = \sin \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = \sin \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 0.062},$$
- $$b_1 = 2 \cdot \cos \left( {2{\rm{\pi }}\cdot{T}/{T_0 }} \right) = 2 \cdot \cos \left( {3.6^ \circ } \right) \hspace{0.15cm} \underline{\approx 1.996}.$$