Difference between revisions of "Aufgaben:Exercise 3.5: Triangular and Trapezoidal Signal"
m (Text replacement - "[[Stochastische_Signaltheorie/" to "[[Theory_of_Stochastic_Signals/") |
m (Text replacement - "rms value" to "standard deviation") |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Uniformly_Distributed_Random_Variables |
}} | }} | ||
| − | [[File:P_ID125__Sto_A_3_5.png|right|frame| | + | [[File:P_ID125__Sto_A_3_5.png|right|frame|Rectangle signal, triangle signal <br>and trapezoid signal ]] |
| − | + | We start from the rectangular signal $x(t)$ according to the upper graph. | |
| − | * | + | *The amplitude values are $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$. |
| − | * | + | *Let the duration of a rectangle and the distance between two successive rectangular pulses be equal to each $T$. |
| − | * | + | *The random variable $x$ – the instantaneous value of the rectangular signal $x(t)$ – thus has the characteristic values (mean, standard deviation): |
:$$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$ | :$$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$ | ||
| − | + | If we now apply this signal to a linear filter with the impulse response | |
| − | :$$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm | + | :$$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T} \\\ 0 & {\rm else} \end{array} \right. , $$ |
| − | + | then the triangular signal $y_1(t) = x(t) \star h_1(t)$ is obtained at its output according to the convolution with | |
| − | * | + | *the minimum values $0\hspace{0.05cm} \rm V$ $($at $t = 0, 2T, 4T, $ ...$)$, |
| − | * | + | *the maximum values $2\hspace{0.05cm} \rm V$ $($at $t = T, 3T, 5T, $ ...$)$. |
| − | + | Thus, this low-pass filter is an integrator over the time duration $T$.<br> | |
| − | + | If, on the other hand, we apply the signal $x(t)$ to the input of a filter with the impulse response | |
| − | :$$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm | + | :$$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T/2} \\\ 0 & {\rm else} \end{array} \right. , $$ |
| − | so | + | so the trapezoidal signal $y_2(t) = x(t) \star h_2(t)$. This second filter thus acts as an integrator over the time duration $T/2$. |
<br> | <br> | ||
| Line 31: | Line 31: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Uniformly_Distributed_Random_Variables|Uniformly distributed random variables]]. |
| − | * | + | *For the corresponding frequency responses $H_1(f=0)= 1$ or $H_2(f=0)= 0.5$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $y_1(t)$ | + | + $y_1(t)$ is a continuous valued random variable. |
| − | - $y_1(t)$ | + | - $y_1(t)$ has a triangular PDF. |
| − | + $y_1(t)$ | + | + $y_1(t)$ is uniformly distributed. |
| − | + $y_2(t)$ | + | + $y_2(t)$ has continuous and discrete valued components. |
| − | { | + | {How large is the uniform part of the signal $y_1(t)$? Check this value $m_{y1}$ also by using the variables $m_x$ and $H_1(f=0)$. |
|type="{}"} | |type="{}"} | ||
| − | $m_{y1} \ = \ $ | + | $m_{y1} \ = \ $ { 1 3% } $\ \rm V$ |
| − | { | + | {Determine the power of the signal $y_1(t)$ by both time averaging and coulter averaging. |
|type="{}"} | |type="{}"} | ||
$P_{y1} \ = \ $ { 1.333 3% } $\ \rm V^2$ | $P_{y1} \ = \ $ { 1.333 3% } $\ \rm V^2$ | ||
| − | { | + | {What is the standard deviation of the signal $y_1(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_{y1} \ = \ $ | + | $\sigma_{y1} \ = \ $ { 0.577 3% } $\ \rm V$ |
| − | { | + | {What is the probability that $y_1(t)$ is larger than $0.75\hspace{0.05cm} \rm V$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 62.5 3% } $ \ \%$ | ${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 62.5 3% } $ \ \%$ | ||
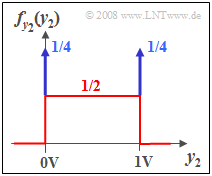
| − | { | + | {Determine the PDF of the signal $y_2(t)$ and sketch it. As a check, enter the PDF value at the point $y_2 = 0.5\hspace{0.05cm} \rm V$. |
|type="{}"} | |type="{}"} | ||
| − | $f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \ = \ $ | + | $f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \ = \ $ { 0.5 3% } $\ \rm 1/V$ |
| − | { | + | {What is the DC component of the signal $y_2(t)$? Check this value $m_{y2}$ also using the quantities $m_x$ and $H_2(f=0)$. |
|type="{}"} | |type="{}"} | ||
$m_{y2} \ = \ ${ 0.5 3% } $\ \rm V$ | $m_{y2} \ = \ ${ 0.5 3% } $\ \rm V$ | ||
| − | { | + | {What is the standard deviation of the signal $y_2(t)$? |
|type="{}"} | |type="{}"} | ||
$\sigma_{y2} \ = \ $ { 0.409 3% } $\ \rm V$ | $\sigma_{y2} \ = \ $ { 0.409 3% } $\ \rm V$ | ||
| − | { | + | {What is the probability that $y_2(t)$ is larger than $0.75\hspace{0.05cm} \rm V$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}(y_2 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 37.5 3% } $ \ \%$ | ${\rm Pr}(y_2 > 0.75\hspace{0.05cm} \rm V) \ = \ $ { 37.5 3% } $ \ \%$ | ||
| Line 91: | Line 91: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID121__Sto_A_3_5_a_neu.png|right|frame| | + | [[File:P_ID121__Sto_A_3_5_a_neu.png|right|frame|Amplitude limit, <br>readable in the PDF]] |
| − | '''(1)''' | + | '''(1)''' Correct are <u>the proposed solutions 1, 3 and 4</u>: |
| − | * | + | *The random variable $y_1$ is uniformly distributed and thus just like $x$ also a continuous valued random variable. |
| − | * | + | *The PDF of $y_2$ exhibits discrete proportions at $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$ on. |
| − | * | + | *There are, of course, continuous valued components between these two boundaries. |
| − | *In | + | *In this domain holds $f_{y2}(y_2) = 1/2$. |
| − | '''(2)''' | + | '''(2)''' The linear mean $m_x = 1\hspace{0.05cm} \rm V$ can be read directly from the data sketch, but could also be formally calculated using the equation for the uniform distribution $($between $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V)$. Another solution is provided by the relation: |
:$$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 1 \hspace{0.15cm}\underline{ =\rm 1\hspace{0.05cm} \rm V}.$$ | :$$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 1 \hspace{0.15cm}\underline{ =\rm 1\hspace{0.05cm} \rm V}.$$ | ||
| − | + | '''(3)''' Actually, the averaging should be done over the whole time domain (both sides to infinity). | |
| − | '''(3)''' | + | * However, for reasons of symmetry, the averaging over the time interval $0 \le t \le T$ is sufficient: |
| − | * | ||
:$$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}{\rm (}\it t{\rm {\rm )}}^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T}{\rm )}^{\rm 2} \hspace{0.1cm}{\rm d} t | :$$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}{\rm (}\it t{\rm {\rm )}}^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T}{\rm )}^{\rm 2} \hspace{0.1cm}{\rm d} t | ||
| − | = \rm {4}/{3}\, V^2 | + | = \rm {4}/{3}\, V^2 \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$ |
| − | * | + | *Sharp averaging gives the same result. Using the PDF $f_{y1}(y_1) = 1/(2\hspace{0.05cm} \rm V)$ namely: |
:$$P_{y_{\rm 1}}= | :$$P_{y_{\rm 1}}= | ||
\int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}{\rm (}\it y_{\rm 1}{\rm )}\it \hspace{0.1cm}{\rm d}y_{\rm 1} | \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}{\rm (}\it y_{\rm 1}{\rm )}\it \hspace{0.1cm}{\rm d}y_{\rm 1} | ||
| Line 119: | Line 118: | ||
| − | + | '''(4)''' The variance can be determined using Steiner's theorem: | |
| − | '''(4)''' | ||
:$$4/3\hspace{0.05cm} \rm V^2 - 1\hspace{0.05cm} \rm V^2 = 1/3\hspace{0.05cm} \rm V^2.$$ | :$$4/3\hspace{0.05cm} \rm V^2 - 1\hspace{0.05cm} \rm V^2 = 1/3\hspace{0.05cm} \rm V^2.$$ | ||
| − | * | + | *The root of this is the standard deviation (standard deviation) we are looking for: |
:$$\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$$ | :$$\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$$ | ||
| − | + | '''(5)''' The probability we are looking for is the integral over the PDF of $0.75\hspace{0.05cm} \rm V$ to $2\hspace{0.05cm} \rm V$, i.e. | |
| − | '''(5)''' | ||
:$${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{ = 62.5\%}.$$ | :$${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{ = 62.5\%}.$$ | ||
| − | + | '''(6)''' The PDF consists of two Dirac delta functions at $0\hspace{0.05cm} \rm V$ and $1\hspace{0.05cm} \rm V$ $($each with weight $1/4)$ and a constant continuous component of | |
| − | '''(6)''' | + | :$$f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{=0.5 \cdot\rm 1/V}.$$ |
| − | :$$f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{=0.5 | + | *At $y_2 = 0.5 \hspace{0.05cm} \rm V$ there is therefore only the continuous part. |
| − | * | ||
| − | + | '''(7)''' The mean value $m_{y_{\rm 2}}\hspace{0.15cm}\underline{ =\rm 0.5\hspace{0.05cm} \rm V}$ can be read directly from the above PDF sketch or calculated as in subtask '''(2)''' as follows: | |
| − | '''(7)''' | ||
:$$m_{y_{\rm 2}} = m_x\cdot H_{\rm 2}( f = 0) = 1\hspace{0.05cm} \rm V \cdot 0.5 {\hspace{0.1cm} = \rm 0.5\hspace{0.05cm} \rm V}.$$ | :$$m_{y_{\rm 2}} = m_x\cdot H_{\rm 2}( f = 0) = 1\hspace{0.05cm} \rm V \cdot 0.5 {\hspace{0.1cm} = \rm 0.5\hspace{0.05cm} \rm V}.$$ | ||
| − | + | '''(8)''' With the above PDF, for given power: | |
| − | '''(8)''' | ||
:$$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}{\rm (}\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 | :$$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}{\rm (}\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 | ||
= 5/12 \,V^2 | = 5/12 \,V^2 | ||
\hspace{0.15cm}{ =\rm 0.417\,V^2}.$$ | \hspace{0.15cm}{ =\rm 0.417\,V^2}.$$ | ||
| − | * | + | *The first part goes back to the continuous PDF, the second part to the PDF Dirac function at $1\hspace{0.05cm} \rm V$. |
| − | * | + | *The Dirac function at $0\hspace{0.05cm} \rm V$ does not contribute to the power. It follows for the standard deviation: |
:$$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= | :$$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= | ||
\sqrt{{\rm 1}/{\rm 6}\rm V^2} | \sqrt{{\rm 1}/{\rm 6}\rm V^2} | ||
| Line 155: | Line 149: | ||
| + | '''(9)''' This probability is also composed of two parts: | ||
| + | :$${\rm Pr}(y_2 > 0.75 {\rm V} ) = {\rm Pr}(0.75 {\rm V} \le y_2 < 1 {\rm V} ) + {\rm Pr}(y_2 = 1 {\rm V} ) = \frac{1}{2} \cdot \frac{1}{4}+ \frac{1}{4} = \frac{3}{8}\hspace{0.15cm}\underline{ = 37.5\%}. $$ | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 163: | Line 157: | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^3.4 Uniformly Distributed Random Variable^]] |
Latest revision as of 12:11, 17 February 2022
We start from the rectangular signal $x(t)$ according to the upper graph.
- The amplitude values are $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$.
- Let the duration of a rectangle and the distance between two successive rectangular pulses be equal to each $T$.
- The random variable $x$ – the instantaneous value of the rectangular signal $x(t)$ – thus has the characteristic values (mean, standard deviation):
- $$m_x = \sigma_x = 1\hspace{0.05cm} \rm V.$$
If we now apply this signal to a linear filter with the impulse response
- $$h_{\rm 1}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T} \\\ 0 & {\rm else} \end{array} \right. , $$
then the triangular signal $y_1(t) = x(t) \star h_1(t)$ is obtained at its output according to the convolution with
- the minimum values $0\hspace{0.05cm} \rm V$ $($at $t = 0, 2T, 4T, $ ...$)$,
- the maximum values $2\hspace{0.05cm} \rm V$ $($at $t = T, 3T, 5T, $ ...$)$.
Thus, this low-pass filter is an integrator over the time duration $T$.
If, on the other hand, we apply the signal $x(t)$ to the input of a filter with the impulse response
- $$h_{\rm 2}(t)=\left \{ \begin{array}{*{4}{c}} 1/T & {\; \rm for}\hspace{0.2cm}{ 0\le t \le T/2} \\\ 0 & {\rm else} \end{array} \right. , $$
so the trapezoidal signal $y_2(t) = x(t) \star h_2(t)$. This second filter thus acts as an integrator over the time duration $T/2$.
Hints:
- This exercise belongs to the chapter Uniformly distributed random variables.
- For the corresponding frequency responses $H_1(f=0)= 1$ or $H_2(f=0)= 0.5$.
Questions
Solution
(1) Correct are the proposed solutions 1, 3 and 4:
- The random variable $y_1$ is uniformly distributed and thus just like $x$ also a continuous valued random variable.
- The PDF of $y_2$ exhibits discrete proportions at $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V$ on.
- There are, of course, continuous valued components between these two boundaries.
- In this domain holds $f_{y2}(y_2) = 1/2$.
(2) The linear mean $m_x = 1\hspace{0.05cm} \rm V$ can be read directly from the data sketch, but could also be formally calculated using the equation for the uniform distribution $($between $0\hspace{0.05cm} \rm V$ and $2\hspace{0.05cm} \rm V)$. Another solution is provided by the relation:
- $$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}( f= 0) = 1\hspace{0.05cm} \rm V \cdot 1 \hspace{0.15cm}\underline{ =\rm 1\hspace{0.05cm} \rm V}.$$
(3) Actually, the averaging should be done over the whole time domain (both sides to infinity).
- However, for reasons of symmetry, the averaging over the time interval $0 \le t \le T$ is sufficient:
- $$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}{\rm (}\it t{\rm {\rm )}}^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T}{\rm )}^{\rm 2} \hspace{0.1cm}{\rm d} t = \rm {4}/{3}\, V^2 \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$
- Sharp averaging gives the same result. Using the PDF $f_{y1}(y_1) = 1/(2\hspace{0.05cm} \rm V)$ namely:
- $$P_{y_{\rm 1}}= \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}{\rm (}\it y_{\rm 1}{\rm )}\it \hspace{0.1cm}{\rm d}y_{\rm 1} =\rm\frac{1}{2V}\cdot \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\hspace{0.1cm}{\rm d}y_{\rm 1} =\rm \frac{8\,{\rm V^3}}{3 \cdot 2\,{\rm V}} \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$
(4) The variance can be determined using Steiner's theorem:
- $$4/3\hspace{0.05cm} \rm V^2 - 1\hspace{0.05cm} \rm V^2 = 1/3\hspace{0.05cm} \rm V^2.$$
- The root of this is the standard deviation (standard deviation) we are looking for:
- $$\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$$
(5) The probability we are looking for is the integral over the PDF of $0.75\hspace{0.05cm} \rm V$ to $2\hspace{0.05cm} \rm V$, i.e.
- $${\rm Pr}(y_1 > 0.75\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{ = 62.5\%}.$$
(6) The PDF consists of two Dirac delta functions at $0\hspace{0.05cm} \rm V$ and $1\hspace{0.05cm} \rm V$ $($each with weight $1/4)$ and a constant continuous component of
- $$f_{y2}(y_2= 0.5\hspace{0.05cm} \rm V) \hspace{0.15cm}\underline{=0.5 \cdot\rm 1/V}.$$
- At $y_2 = 0.5 \hspace{0.05cm} \rm V$ there is therefore only the continuous part.
(7) The mean value $m_{y_{\rm 2}}\hspace{0.15cm}\underline{ =\rm 0.5\hspace{0.05cm} \rm V}$ can be read directly from the above PDF sketch or calculated as in subtask (2) as follows:
- $$m_{y_{\rm 2}} = m_x\cdot H_{\rm 2}( f = 0) = 1\hspace{0.05cm} \rm V \cdot 0.5 {\hspace{0.1cm} = \rm 0.5\hspace{0.05cm} \rm V}.$$
(8) With the above PDF, for given power:
- $$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}{\rm (}\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 = 5/12 \,V^2 \hspace{0.15cm}{ =\rm 0.417\,V^2}.$$
- The first part goes back to the continuous PDF, the second part to the PDF Dirac function at $1\hspace{0.05cm} \rm V$.
- The Dirac function at $0\hspace{0.05cm} \rm V$ does not contribute to the power. It follows for the standard deviation:
- $$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= \sqrt{{\rm 1}/{\rm 6}\rm V^2} \hspace{0.15cm}\underline{=0.409\, \rm V}.$$
(9) This probability is also composed of two parts:
- $${\rm Pr}(y_2 > 0.75 {\rm V} ) = {\rm Pr}(0.75 {\rm V} \le y_2 < 1 {\rm V} ) + {\rm Pr}(y_2 = 1 {\rm V} ) = \frac{1}{2} \cdot \frac{1}{4}+ \frac{1}{4} = \frac{3}{8}\hspace{0.15cm}\underline{ = 37.5\%}. $$