Aufgaben:Exercise 4.1: PCM System 30/32

• Return to book

Binärdarstellung mit Dualcode

Über viele Jahre wurde in Deutschland das PCM–System 30/32 eingesetzt, das folgende Spezifikationen aufweist:

• Es erlaubt die digitale Übertragung von 30 Sprachkanälen im Zeitmultiplex zusammen mit je einem Sychronisations– und Wählzeichenkanal   ⇒   die Gesamtkanalzahl ist  $Z = 32$.
• Jeder einzelne Sprachkanal ist auf den Frequenzbereich von  $300 \ \rm Hz$  bis  $3400 \ \rm Hz$  bandbegrenzt.
• Jeder einzelne Abtastwert wird durch  $N = 8$  Bit dargestellt, wobei vom so genannten Dualcode ausgegangen wird.
• Die Gesamtbitrate beträgt  $R_{\rm B} = 2.048 \ \rm Mbit/s$.

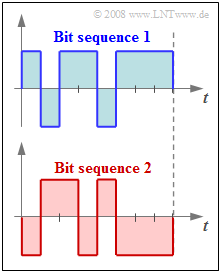
Die Grafik zeigt die Binärdarstellung zweier willkürlich ausgewählter Abtastwerte.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Pulscodemodulation.
• Bezug genommen wird insbesondere auf die Seite  PCM-Codierung und -Decodierung.

• Für die Lösung der Teilaufgabe  (2)  ist vorauszusetzen:  Alle Sprachsignale sind normiert und auf den Bereich  $±1$  amplitudenbegrenzt.

Fragebogen

1

Wie groß ist die Quantisierungsstufenzahl  $M$?

$M \ = \ $

2

Wie wird der Abtastwert  $-0.182$  dargestellt? Mit

	der Bitfolge 1,
	der Bitfolge 2,
	keiner von beiden.

3

Wie groß ist die Bitdauer  $T_{\rm B}$?

$T_{\rm B} \ = \ $ $\ \rm µ s$

4

In welchem Abstand  $T_{\rm A}$  werden die Sprachsignale abgetastet?

$T_{\rm A} \ = \ $ $\ \rm µ s$

5

Wie groß ist die Abtastrate  $f_{\rm A}$?

$f_{\rm A} \ = \ $ $\ \rm kHz$

6

Welche der folgenden Aussagen ist richtig?

	Das Abtasttheorem wird nicht erfüllt.
	Das Abtasttheorem wird gerade noch erfüllt.
	Die Abtastfrequenz ist größer als der kleinstmögliche Wert.

Musterlösung

Solution

(1)  Mit  $N = 8$  Bit können insgesamt  $2^8$  Quantisierungsintervalle dargestellt werden   ⇒   $\underline{M = 256}$.

(2)  Nummeriert man die Quantisierungsintervalle von  $0$  bis  $255$, so steht die "Bitfolge 1" für

$$ \mu_1 = 2^7 + 2^5 +2^4 +2^2 +2^1 +2^0 = 255 -2^6 -2^3 = 183\hspace{0.05cm},$$

und die "Bitfolge 2" für

$$\mu_2 = 2^6 + 2^5 +2^3 = 104\hspace{0.05cm}.$$

• Mit dem Wertebereich  $±1$  hat jedes Quantisierungsintervall die Breite  ${\it Δ} = 1/128$.
• Der Index  $μ = 183$  steht somit für das Intervall von  $183/128 - 1 = 0.4297$  bis  $184/128 - 1 = 0.4375$.
• $μ = 104$  kennzeichnet das Intervall von  $-0.1875$  bis  $-0.1797$.
• Der Abtastwert $–0.182$ wird somit durch die Bitfolge 2 dargestellt.

(3)  Die Bitdauer  $T_{\rm B}$  ist der Kehrwert der Bitrate  $R_{\rm B}$:

$$T_{\rm B} = \frac{1}{R_{\rm B} }= \frac{1}{2.048 \cdot 10^6\,{\rm 1/s} } \hspace{0.15cm}\underline {= 0.488\,{\rm µ s}} \hspace{0.05cm}.$$

(4)  Während der Zeitdauer  $T_{\rm A}$  werden  $Z · N$  Binärsymbole übertragen:

$$T_{\rm A} = Z \cdot N \cdot {T_{\rm B} } = 32 \cdot 8 \cdot 0.488\,{\rm µ s} \hspace{0.15cm}\underline {= 125\,{\rm µ s}} \hspace{0.05cm}.$$

(5)  Den Kehrwert von  $T_{\rm A}$  bezeichnet man als die Abtastrate:

$$f_{\rm A} = \frac{1}{T_{\rm A} } \hspace{0.15cm}\underline {= 8\,{\rm kHz}} \hspace{0.05cm}.$$

(6)  Das Abtasttheorem wäre bereits mit  $f_{\rm A} ≥ 2 · f_\text{N, max} = 6.8 \ \rm kHz$  erfüllt.  Richtig ist somit der letzte Lösungsvorschlag.