Difference between revisions of "Aufgaben:Exercise 4.09: Cyclo-Ergodicity"
From LNTwww
| (9 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Auto-Correlation_Function |
}} | }} | ||
| − | [[File:P_ID379__Sto_A_4_9.png|right|frame| | + | [[File:P_ID379__Sto_A_4_9.png|right|frame|"Cyclo–ergodicity property"]] |
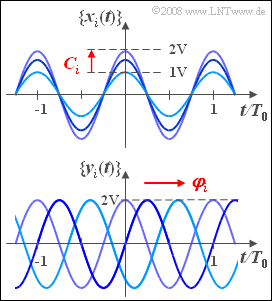
| − | + | We consider two different random processes whose pattern functions are harmonic oscillations, each with the same frequency $f_0 = 1/T_0$, where $T_0$ denotes the period duration. | |
| − | * | + | *In the random process $\{x_i(t)\}$ shown above, the stochastic component is the amplitude, where the random parameter $C_i$ can take all values between $1\hspace{0.05cm}\rm V$ and $2\hspace{0.05cm}\rm V$ with equal probability: |
| − | :$$\{ x_i(t) \} = \{ C_i \cdot \cos (2 \pi | + | :$$\{ x_i(t) \} = \{ C_i \cdot \cos (2 \pi f_{\rm 0} t)\}. $$ |
| − | * | + | *In the process $\{y_i(t)\}$, all pattern functions have the same amplitude: $x_0 = 2\hspace{0.05cm}\rm V$. Here the phase $\varphi_i$ varies, which averaged over all pattern functions is uniformly distributed between $0$ and $2\pi$ |
| − | :$$\{ y_i(t) \} = \{ x_{\rm 0} \cdot \cos (2 \pi | + | :$$\{ y_i(t) \} = \{ x_{\rm 0} \cdot \cos (2 \pi f_{\rm 0} t - \varphi_i)\}. $$ |
| − | + | The properties "cyclo-stationary" and "cyclo-ergodic" state, | |
| − | * | + | *that although the processes cannot be described as stationary and ergodic in the strict sense, |
| − | * | + | *but all statistical characteristics are the same for multiples of the period duration $T_0$ in each case. |
| − | In | + | In these cases, most of the calculation rules, which actually apply only to ergodic processes, are also applicable. |
| − | + | '''Hint''': This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '' | ||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The process $\{x_i(t)\}$ is stationary. |
| − | - | + | - The process $\{x_i(t)\}$ is ergodic. |
| − | + | + | + The process $\{y_i(t)\}$ is stationary. |
| − | + | + | + The process $\{y_i(t)\}$ is ergodic. |
| − | { | + | {Calculate the auto-correlation function $\varphi_y(\tau)$ for different $\tau$ values. |
|type="{}"} | |type="{}"} | ||
$\varphi_y(\tau=0)\ = \ $ { 2 3% } $\ \rm V^2$ | $\varphi_y(\tau=0)\ = \ $ { 2 3% } $\ \rm V^2$ | ||
| − | $\varphi_y(\tau=0.25 \cdot T_0)\ = | + | $\varphi_y(\tau=0.25 \cdot T_0)\ = \ $ { 0. } $\ \rm V^2$ |
| − | $\varphi_y(\tau=1.50 \cdot T_0)\ = | + | $\varphi_y(\tau=1.50 \cdot T_0)\ = \ $ { -2.06--1.94 }$\ \rm V^2$ |
| − | { | + | {Which of the following statements are true regarding $\{y_i(t)\}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + All pattern signals are free of DC signals. |
| − | + | + | + All pattern signals have the rms value $2\hspace{0.05cm}\rm V$. |
| − | - | + | - The ACF has twice the period $(2T_0)$ as the pattern signals $(T_0)$. |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>proposed solutions 3 and 4</u>: |
| − | * | + | *At time $t = 0$ $($and all multiples of the period $T_0)$ each pattern signal $x_i(t)$ has a value between $1\hspace{0.05cm}\rm V$ and $2\hspace{0.05cm}\rm V$. The mean value is $1.5\hspace{0.05cm}\rm V$. |
| − | * | + | *In contrast, for $t = T_0/4$ the signal value of the entire ensemble is identically zero. That is: <br> Even the linear mean does not satisfy the stationarity condition: The process $\{x_i(t)\}$ is not stationary and therefore cannot be ergodic. |
| − | + | *In contrast, for the process $\{y_i(t)\}$ the same moments are expected at all times due to the uniformly distributed phase ⇒ the process is stationary. | |
| − | * | + | *Since the phase relations are lost in the ACF calculation, each individual pattern function is representative of the entire process. Therefore, ergodicity can be hypothetically assumed here. |
| − | * | + | *At the end of the exercise, check whether this assumption is justified. |
| − | * | ||
| − | '''(2)''' | + | '''(2)''' Due to ergodicity, any pattern function can be used for ACF calculation. We arbitrarily use here the phase $\varphi_i = 0$. |
| − | * | + | *Because of the periodicity, it is sufficient to report only one period $T_0$. Then holds: |
:$$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$ | :$$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$ | ||
| + | *Using the trigonometric relation $\cos (\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \cos (\alpha + \beta) + {1}/{2} \cdot \cos (\alpha - \beta)$ it further follows: | ||
| + | :$$\varphi_y (\tau) = \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (4 \pi \it{f_{\rm 0} t} + {\rm 2} \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t \ {\rm +} \ \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (-2 \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t. $$ | ||
| + | *The first integral is zero (integration over two periods of the cosine function). The second integrand is independent of the integration variable $t$. It follows: | ||
| + | :$$\varphi_y (\tau) ={{ x}_0^2}/{\rm 2} \cdot \cos (2 \pi {f_{\rm 0} \tau}). $$ | ||
| + | *For the given time points, with $x_0 = 2\hspace{0.05cm}\rm V$: | ||
| + | :$$\varphi_y (0)\hspace{0.15cm}\underline{ = 2\hspace{0.05cm}{\rm V}^2}, \hspace{0.5cm} \varphi_y (0.25 \cdot { T}_{\rm 0}{\rm )} \hspace{0.15cm}\underline{ = 0}, \hspace{0.5cm} \varphi_y (\rm 1.5 \cdot {\it T}_{\rm 0} {\rm )} \hspace{0.15cm}\underline{= \rm -2\hspace{0.05cm}{\rm V}^2}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''(3)''' | + | '''(3)''' Correct are <u>both first proposed solutions</u>: |
| − | * | + | *The mean $m_y$ can be obtained from the limit of the ACF for $\tau \to \infty$ if one excludes the periodic parts. It follows $m_y= 0$. |
| − | * | + | *The variance (power) is equal to the ACF value at the point $\tau = 0$ ⇒ $\sigma_y^2 =2\hspace{0.05cm}\rm V^2$. The rms value is the square root of it: $\sigma_y \approx 1.414\hspace{0.05cm}\rm V$. |
| − | * | + | *The period of a periodic random process is preserved in the ACF, that is, the period of the ACF is also $T_0$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^4.4 Auto-Correlation Function^]] |
Latest revision as of 17:00, 19 March 2022
We consider two different random processes whose pattern functions are harmonic oscillations, each with the same frequency $f_0 = 1/T_0$, where $T_0$ denotes the period duration.
- In the random process $\{x_i(t)\}$ shown above, the stochastic component is the amplitude, where the random parameter $C_i$ can take all values between $1\hspace{0.05cm}\rm V$ and $2\hspace{0.05cm}\rm V$ with equal probability:
- $$\{ x_i(t) \} = \{ C_i \cdot \cos (2 \pi f_{\rm 0} t)\}. $$
- In the process $\{y_i(t)\}$, all pattern functions have the same amplitude: $x_0 = 2\hspace{0.05cm}\rm V$. Here the phase $\varphi_i$ varies, which averaged over all pattern functions is uniformly distributed between $0$ and $2\pi$
- $$\{ y_i(t) \} = \{ x_{\rm 0} \cdot \cos (2 \pi f_{\rm 0} t - \varphi_i)\}. $$
The properties "cyclo-stationary" and "cyclo-ergodic" state,
- that although the processes cannot be described as stationary and ergodic in the strict sense,
- but all statistical characteristics are the same for multiples of the period duration $T_0$ in each case.
In these cases, most of the calculation rules, which actually apply only to ergodic processes, are also applicable.
Hint: This exercise belongs to the chapter Auto-Correlation Function.
Questions
Solution
(1) Correct are the proposed solutions 3 and 4:
- At time $t = 0$ $($and all multiples of the period $T_0)$ each pattern signal $x_i(t)$ has a value between $1\hspace{0.05cm}\rm V$ and $2\hspace{0.05cm}\rm V$. The mean value is $1.5\hspace{0.05cm}\rm V$.
- In contrast, for $t = T_0/4$ the signal value of the entire ensemble is identically zero. That is:
Even the linear mean does not satisfy the stationarity condition: The process $\{x_i(t)\}$ is not stationary and therefore cannot be ergodic. - In contrast, for the process $\{y_i(t)\}$ the same moments are expected at all times due to the uniformly distributed phase ⇒ the process is stationary.
- Since the phase relations are lost in the ACF calculation, each individual pattern function is representative of the entire process. Therefore, ergodicity can be hypothetically assumed here.
- At the end of the exercise, check whether this assumption is justified.
(2) Due to ergodicity, any pattern function can be used for ACF calculation. We arbitrarily use here the phase $\varphi_i = 0$.
- Because of the periodicity, it is sufficient to report only one period $T_0$. Then holds:
- $$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$
- Using the trigonometric relation $\cos (\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \cos (\alpha + \beta) + {1}/{2} \cdot \cos (\alpha - \beta)$ it further follows:
- $$\varphi_y (\tau) = \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (4 \pi \it{f_{\rm 0} t} + {\rm 2} \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t \ {\rm +} \ \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (-2 \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t. $$
- The first integral is zero (integration over two periods of the cosine function). The second integrand is independent of the integration variable $t$. It follows:
- $$\varphi_y (\tau) ={{ x}_0^2}/{\rm 2} \cdot \cos (2 \pi {f_{\rm 0} \tau}). $$
- For the given time points, with $x_0 = 2\hspace{0.05cm}\rm V$:
- $$\varphi_y (0)\hspace{0.15cm}\underline{ = 2\hspace{0.05cm}{\rm V}^2}, \hspace{0.5cm} \varphi_y (0.25 \cdot { T}_{\rm 0}{\rm )} \hspace{0.15cm}\underline{ = 0}, \hspace{0.5cm} \varphi_y (\rm 1.5 \cdot {\it T}_{\rm 0} {\rm )} \hspace{0.15cm}\underline{= \rm -2\hspace{0.05cm}{\rm V}^2}.$$
(3) Correct are both first proposed solutions:
- The mean $m_y$ can be obtained from the limit of the ACF for $\tau \to \infty$ if one excludes the periodic parts. It follows $m_y= 0$.
- The variance (power) is equal to the ACF value at the point $\tau = 0$ ⇒ $\sigma_y^2 =2\hspace{0.05cm}\rm V^2$. The rms value is the square root of it: $\sigma_y \approx 1.414\hspace{0.05cm}\rm V$.
- The period of a periodic random process is preserved in the ACF, that is, the period of the ACF is also $T_0$.