Aufgaben:Exercise 4.1: PCM System 30/32

• Return to book

binary display with dual code

For many years, the PCM system 30/32 was used in Germany, which has the following specifications:

• It allows digital transmission of 30 voice channels in time division multiplex together with one each of synchronization and dial character channels   ⇒   the total number of channels is  $Z = 32$.
• Each individual voice channel is bandlimited to the frequency range of  $300 \ \rm Hz$  to  $3400 \ \rm Hz$  .
• Each individual sample is represented by  $N = 8$  bits, assuming the so-called dual code.
• The total bit rate is  $R_{\rm B} = 2.048 \rm Mbit/s$.

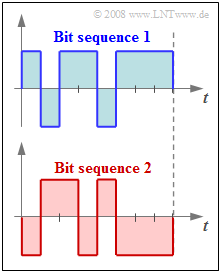
The graph shows the binary representation of two arbitrarily selected samples.

Hints:

• The exercise belongs to the chapter  Pulse Code Modulation.
• Reference is made in particular to the page  PCM encoding and decoding.

• For the solution of the subtask  (2)  it is to be assumed:  All speech signals are normalized and limited to the range  $±1$  amplitude.

Questions

1

What is the quantization step number  $M$?

$M \ = \ $

2

How is the sample value  $-0.182$  represented? With

	the bit sequence 1,
	the bit sequence 2,
	neither of them.

3

What is the bit duration  $T_{\rm B}$?

$T_{\rm B} \ = \ $ $\ \rm µ s$

4

At what distance  $T_{\rm A}$  are the speech signals sampled?

$T_{\rm A} \ = \ $ $\ \rm µ s$

5

What is the sampling rate  $f_{\rm A}$?

$f_{\rm A} \ = \ $ $\ \rm kHz$

6

Which of the following statements is correct?

	The sampling theorem is not satisfied.
	The sampling theorem is just fulfilled.
	The sampling frequency is greater than the smallest possible value.

Solution

Solution

(1)  With  $N = 8$  bits a total of  $2^8$  quantization intervals can be represented   ⇒   $\underline{M = 256}$.

(2)  Numbering the quantization intervals from  $0$  to  $255$, the "bit sequence 1" represents.

$$ \mu_1 = 2^7 + 2^5 +2^4 +2^2 +2^1 +2^0 = 255 -2^6 -2^3 = 183\hspace{0.05cm},$$

and the "bit sequence 2" for

$$\mu_2 = 2^6 + 2^5 +2^3 = 104\hspace{0.05cm}.$$

• With the value range  $±1$  each quantization interval has width  ${\it Δ} = 1/128$.
• The index  $μ = 183$  thus represents the interval from  $183/128 - 1 = 0.4297$  to  $184/128 - 1 = 0.4375$.
• $μ = 104$  denotes the interval from  $-0.1875$  to  $-0.1797$.
• The sample $-0.182$ is thus represented by the bit sequence 2.

(3)  The bit duration  $T_{\rm B}$  is the reciprocal of the bit rate  $R_{\rm B}$:

$$T_{\rm B} = \frac{1}{R_{\rm B} }= \frac{1}{2.048 \cdot 10^6\,{\rm 1/s} } \hspace{0.15cm}\underline {= 0.488\,{\rm µ s}} \hspace{0.05cm}.$$

(4)  During duration  $T_{\rm A}$  binary symbols are transmitted  $Z \cdot N$ :

$$T_{\rm A} = Z \cdot N \cdot {T_{\rm B} } = 32 \cdot 8 \cdot 0.488\,{\rm µ s} \hspace{0.15cm}\underline {= 125\,{\rm µ s}} \hspace{0.05cm}.$$

(5)  The reciprocal of  $T_{\rm A}$  is called the sampling rate:

$$f_{\rm A} = \frac{1}{T_{\rm A} } \hspace{0.15cm}\underline {= 8\,{\rm kHz}} \hspace{0.05cm}.$$

(6)  The sampling theorem would already be given by  $f_{\rm A} ≥ 2 \cdot f_\text{N, max} = 6.8 \ \rm kHz$  Thus the last proposed solution is correct.