Aufgaben:Exercise 4.2: Low-Pass for Signal Reconstruction

• Return to book

Continuous and discrete spectrum  (examples)

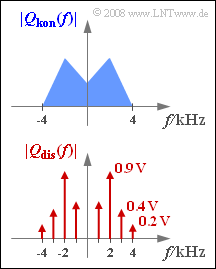
We consider in this exercise two different source signals  $q_{\rm kon}(t)$  and  $q_{\rm dis}(t)$ whose magnitude spectra  $|Q_{\rm kon}(f)|$  and  $|Q_{\rm dis}(f)|$  are plotted.   The highest frequency occurring in the signals is in each case  $4 \rm kHz$.

• Nothing more is known of the spectral function  $Q_{\rm kon}(f)$  than that it is a continuous spectrum, where:

$$Q_{\rm kon}(|f| \le 4\,{\rm kHz}) \ne 0 \hspace{0.05cm}.$$

• The spectrum  $Q_{\rm dis}(f)$  contains spectral lines at  $±1 \ \rm kHz$,  $±2 \ \rm kHz$,  $±3 \ \rm kHz$  and  $±4 \ \rm kHz$.  Thus:

$$q_{\rm dis}(t) = \sum_{i=1}^{4}C_i \cdot \cos (2 \pi \cdot f_i \cdot t - \varphi_i),$$

Amplitude values:   $C_1 = 1.0 \ \rm V$, $C_2 = 1.8 \ \rm V$, $C_3 = 0.8 \ \rm V$, $C_4 = 0.4 \ \rm V.$

The phase values  $φ_1$,  $φ_2$  and  $φ_3$  are respectively in the range  $±18^\circ$  and it holds  $φ_4 = 90^\circ$.

The signals are each sampled at frequency  $f_{\rm A}$  and immediately fed to an ideal rectangular lowpass filter with cutoff frequency  $f_{\rm G}$  This scenario applies, for example, to.

• the interference-free pulse amplitude modulation (PAM) and
• the interference-free pulse code modulation (PCM) at infinitely large quantization stage number  $M$.

The output signal of the (rectangular) low-pass filter is called the sink signal  $v(t)$  and for the error signal 

$$ε(t) = v(t) - q(t).$$

This is different from zero only if the parameters of the sampling  $($sampling frequency $f_{\rm A})$  and/or the signal reconstruction  $($cutoff frequency $f_{\rm G})$  are not dimensioned in the best possible way.

Hints:

• The exercise belongs to the chapter  Pulse Code Modulation.
• Reference is made in particular to the page  Sampling and Signal Reconstruction.

Questions

1

Which statements are true for  $f_{\rm A} = 8\ \rm kHz$  and  $f_{\rm G} = 4\ \rm kHz$ ?

	The signal  $q_{\rm kon}(t)$  can be completely reconstructed:   $ε_{\rm kon}(t) = 0$.
	The signal  $q_{\rm dis}(t)$  can be completely reconstructed:   $ε_{\rm dis}(t) = 0$.

2

Which statements are true for  $f_{\rm A} = 10\ \rm kHz$  and  $f_{\rm G} = 5\ \rm kHz$ ?

	The signal  $q_{\rm dis}(t)$  can be completely reconstructed:   $ε_{\rm dis}(t) = 0$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $4 \rm kHz$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $6 \rm kHz$.

3

Which statements are true for  $f_{\rm A} = 10\ \rm kHz$  and  $f_{\rm G} = 3.5\ \rm kHz$ ?

	The signal  $q_{\rm dis}(t)$  can be completely reconstructed:   $ε_{\rm dis}(t) = 0$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $4 \rm kHz$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $6 \rm kHz$.

4

Which statements are true for  $f_{\rm A} = 10\ \rm kHz$  and  $f_{\rm G} = 6.5\ \rm kHz$?

	The signal  $q_{\rm dis}(t)$  can be completely reconstructed:   $ε_{\rm dis}(t) = 0$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $4 \rm kHz$.
	$ε_{\rm dis}(t)$  is a harmonic oscillation with  $6 \ \rm kHz$.

Solution

Solution

(1)  Only the first statement is correct:

• Sampling  $q_{\rm dis}(t)$  with sampling frequency  $f_{\rm A} = 8 \ \rm kHz$  leads to an irreversible error, since  $Q_{\rm dis}(f)$  involves a discrete spectral component (diracline) at  $f_4 = 4\ \rm kHz$  and the phase value  $φ_4 ≠ 0$  is.
• With the phase value given here  $φ_4 = 90^\circ$  $(4 \ \rm kHz$- sinusoidal component$)$  holds  $ε_{\rm dis}(t) = v_{\rm dis}(t) - q_{\rm dis}(t) = -0. 4 \ \rm V - \sin(2π \cdot f_4 \cdot t)$.  See also sample solution to exercise 4.2Z.
• On the other hand, the signal  $q_{\rm kon}(t)$  with the continuous spectrum  $Q_{\rm kon}(f)$  can also then be measured with a square-wave low-pass filter  $($with cutoff frequency  $f_{\rm G} = 4\ \rm kHz)$  be completely reconstructed if sampling frequency  $f_{\rm A} = 8\ \rm kHz$  was used.   For all frequencies not equal to  $f_4$  the sampling theorem is satisfied.
• But the contribution of the  $f_4$ component to the total spectrum  $Q_{\rm kon}(f)$  is only vanishingly small   ⇒   ${\rm Pr}(f_4) → 0$ as long as the spectrum at  $f_4$  has no diracline.

(2)  Only the proposed solution 1 is correct:

• With  $f_{\rm A} = 10\ \rm kHz$  the sampling theorem is satisfied in both cases.
• With  $f_{\rm G} = f_{\rm A} /2$  both error signals  $ε_{\rm kon}(t)$ and $ε_{\rm dis}(t)$ are identically zero.
• In addition, the signal reconstruction also works as long as  $f_{\rm G} > 4 \ \rm kHz$  and  $f_{\rm G} < 6 \ \rm kHz$  holds.

(3)  The correct solution here is suggested solution 2:

• With  $f_{\rm G} = 3.5 \ \rm kHz$  the lowpass incorrectly removes the  $4\ \rm kHz$ component, that is, then holds:

$$v_{\rm dis}(t) = q_{\rm dis}(t) - 0.4\,{\rm V} \cdot \sin (2 \pi \cdot f_{\rm 4} \cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \varepsilon_{\rm dis}(t) = - 0.4\,{\rm V} \cdot \sin (2 \pi \cdot f_{\rm 4} \cdot t)\hspace{0.05cm}.$$

Signal reconstruction with too large cutoff frequency

(4)  The correct solution here is suggested solution 3:

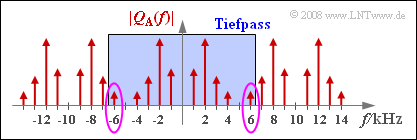
• Sampling with  $f_{\rm A} = 10\ \rm kHz$  yields the periodic spectrum sketched on the right.
• The low pass with  $f_{\rm G} = 6.5 \ \rm kHz$  removes all discrete frequency components with  $|f| ≥ 7\ \rm kHz$, but not the  $6\ \rm kHz$ component.

The error signal  $ε_{\rm dis}(t) = v_{\rm dis}(t) - q_{\rm dis}(t)$  is then a harmonic oscillation with

• the frequency  $f_6 = f_{\rm A} - f_4 = 6\ \rm kHz$,
• the amplitude  $A_4$ of the  $f_4$ component,
• the phase  $φ_{-4} = -φ_4$  of the  $Q(f)$ component at  $f = -f_4$.