Difference between revisions of "Aufgaben:Exercise 4.1: PCM System 30/32"
From LNTwww
| (3 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:EN_Mod_A_4_1.png|right|frame| | + | [[File:EN_Mod_A_4_1.png|right|frame|Binary display with dual code]] |
| − | For many years, the PCM system 30/32 was used in Germany, which has the following specifications: | + | For many years, the '''PCM system 30/32''' was used in Germany, which has the following specifications: |
| − | * It allows digital transmission of 30 voice channels in time division multiplex together with one each of synchronization and dial character | + | * It allows digital transmission of 30 voice channels in time division multiplex together with one channel each of synchronization and dial character ⇒ the total number of channels is $Z = 32$. |
| − | * Each individual voice channel is bandlimited to the frequency range of $300 \ \rm Hz$ to $3400 \ \rm Hz$ | + | * Each individual voice channel is bandlimited to the frequency range of $300 \ \rm Hz$ to $3400 \ \rm Hz$. |
| − | * Each individual sample is represented by $N = 8$ bits, assuming the so-called dual code. | + | * Each individual sample is represented by $N = 8$ bits, assuming the so-called "dual code". |
| − | * The total bit rate is $R_{\rm B} = 2.048 \rm Mbit/s$. | + | * The total bit rate is $R_{\rm B} = 2.048\ \rm Mbit/s$. |
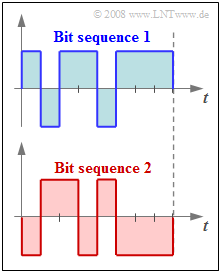
The graph shows the binary representation of two arbitrarily selected samples. | The graph shows the binary representation of two arbitrarily selected samples. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 24: | Line 18: | ||
Hints: | Hints: | ||
*The exercise belongs to the chapter [[Modulation_Methods/Pulse_Code_Modulation|Pulse Code Modulation]]. | *The exercise belongs to the chapter [[Modulation_Methods/Pulse_Code_Modulation|Pulse Code Modulation]]. | ||
| − | *Reference is made in particular to the page [[Modulation_Methods/Pulse_Code_Modulation#PCM_encoding_and_decoding|PCM encoding and decoding]]. | + | *Reference is made in particular to the page [[Modulation_Methods/Pulse_Code_Modulation#PCM_encoding_and_decoding|PCM encoding and decoding]]. |
| − | + | *For the solution of subtask '''(2)''' it is to be assumed: All speech signals are normalized and limited to the amplitude range $±1$. | |
| − | *For the solution of | ||
| Line 37: | Line 30: | ||
| − | {How is the sample value $-0.182$ represented? With | + | {How is the sample value "$-0.182$" represented? With |
|type="()"} | |type="()"} | ||
- the bit sequence 1, | - the bit sequence 1, | ||
| Line 51: | Line 44: | ||
$T_{\rm A} \ = \ $ { 125 3% } $\ \rm µ s$ | $T_{\rm A} \ = \ $ { 125 3% } $\ \rm µ s$ | ||
| − | {What is the sampling rate | + | {What is the sampling rate $f_{\rm A}$? |
|type="{}"} | |type="{}"} | ||
$f_{\rm A} \ = \ $ { 8 3% } $\ \rm kHz$ | $f_{\rm A} \ = \ $ { 8 3% } $\ \rm kHz$ | ||
| Line 70: | Line 63: | ||
| − | '''(2)''' Numbering the quantization intervals from $0$ to $255$, the "bit sequence 1" represents | + | '''(2)''' Numbering the quantization intervals from $0$ to $255$, the "bit sequence 1" represents |
:$$ \mu_1 = 2^7 + 2^5 +2^4 +2^2 +2^1 +2^0 = 255 -2^6 -2^3 = 183\hspace{0.05cm},$$ | :$$ \mu_1 = 2^7 + 2^5 +2^4 +2^2 +2^1 +2^0 = 255 -2^6 -2^3 = 183\hspace{0.05cm},$$ | ||
| − | and the "bit sequence 2" | + | and the "bit sequence 2" represents |
:$$\mu_2 = 2^6 + 2^5 +2^3 = 104\hspace{0.05cm}.$$ | :$$\mu_2 = 2^6 + 2^5 +2^3 = 104\hspace{0.05cm}.$$ | ||
*With the value range $±1$ each quantization interval has width ${\it Δ} = 1/128$. | *With the value range $±1$ each quantization interval has width ${\it Δ} = 1/128$. | ||
*The index $μ = 183$ thus represents the interval from $183/128 - 1 = 0.4297$ to $184/128 - 1 = 0.4375$. | *The index $μ = 183$ thus represents the interval from $183/128 - 1 = 0.4297$ to $184/128 - 1 = 0.4375$. | ||
| − | * $μ = 104$ denotes the interval from $-0.1875$ to $-0.1797$. | + | * $μ = 104$ denotes the interval from "$-0.1875$" to $-0.1797$. |
| − | *The sample $-0.182$ is thus represented by | + | *The sample $-0.182$ is thus represented by <u>bit sequence 2</u>. |
| Line 84: | Line 77: | ||
| − | '''(4)''' During duration $T_{\rm A}$ | + | '''(4)''' During duration $T_{\rm A}$ ⇒ $Z \cdot N$ binary symbols are transmitted: |
:$$T_{\rm A} = Z \cdot N \cdot {T_{\rm B} } = 32 \cdot 8 \cdot 0.488\,{\rm µ s} \hspace{0.15cm}\underline {= 125\,{\rm µ s}} \hspace{0.05cm}.$$ | :$$T_{\rm A} = Z \cdot N \cdot {T_{\rm B} } = 32 \cdot 8 \cdot 0.488\,{\rm µ s} \hspace{0.15cm}\underline {= 125\,{\rm µ s}} \hspace{0.05cm}.$$ | ||
| Line 92: | Line 85: | ||
| − | '''(6)''' The sampling theorem would already be given by $f_{\rm A} ≥ 2 | + | '''(6)''' The sampling theorem would already be given by $f_{\rm A} ≥ 2 \cdot f_\text{N, max} = 6.8 \ \rm kHz$. Thus the <u>last proposed solution</u> is correct. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:23, 7 April 2022
For many years, the PCM system 30/32 was used in Germany, which has the following specifications:
- It allows digital transmission of 30 voice channels in time division multiplex together with one channel each of synchronization and dial character ⇒ the total number of channels is $Z = 32$.
- Each individual voice channel is bandlimited to the frequency range of $300 \ \rm Hz$ to $3400 \ \rm Hz$.
- Each individual sample is represented by $N = 8$ bits, assuming the so-called "dual code".
- The total bit rate is $R_{\rm B} = 2.048\ \rm Mbit/s$.
The graph shows the binary representation of two arbitrarily selected samples.
Hints:
- The exercise belongs to the chapter Pulse Code Modulation.
- Reference is made in particular to the page PCM encoding and decoding.
- For the solution of subtask (2) it is to be assumed: All speech signals are normalized and limited to the amplitude range $±1$.
Questions
Solution
(1) With $N = 8$ bits a total of $2^8$ quantization intervals can be represented ⇒ $\underline{M = 256}$.
(2) Numbering the quantization intervals from $0$ to $255$, the "bit sequence 1" represents
- $$ \mu_1 = 2^7 + 2^5 +2^4 +2^2 +2^1 +2^0 = 255 -2^6 -2^3 = 183\hspace{0.05cm},$$
and the "bit sequence 2" represents
- $$\mu_2 = 2^6 + 2^5 +2^3 = 104\hspace{0.05cm}.$$
- With the value range $±1$ each quantization interval has width ${\it Δ} = 1/128$.
- The index $μ = 183$ thus represents the interval from $183/128 - 1 = 0.4297$ to $184/128 - 1 = 0.4375$.
- $μ = 104$ denotes the interval from "$-0.1875$" to $-0.1797$.
- The sample $-0.182$ is thus represented by bit sequence 2.
(3) The bit duration $T_{\rm B}$ is the reciprocal of the bit rate $R_{\rm B}$:
- $$T_{\rm B} = \frac{1}{R_{\rm B} }= \frac{1}{2.048 \cdot 10^6\,{\rm 1/s} } \hspace{0.15cm}\underline {= 0.488\,{\rm µ s}} \hspace{0.05cm}.$$
(4) During duration $T_{\rm A}$ ⇒ $Z \cdot N$ binary symbols are transmitted:
- $$T_{\rm A} = Z \cdot N \cdot {T_{\rm B} } = 32 \cdot 8 \cdot 0.488\,{\rm µ s} \hspace{0.15cm}\underline {= 125\,{\rm µ s}} \hspace{0.05cm}.$$
(5) The reciprocal of $T_{\rm A}$ is called the sampling rate:
- $$f_{\rm A} = \frac{1}{T_{\rm A} } \hspace{0.15cm}\underline {= 8\,{\rm kHz}} \hspace{0.05cm}.$$
(6) The sampling theorem would already be given by $f_{\rm A} ≥ 2 \cdot f_\text{N, max} = 6.8 \ \rm kHz$. Thus the last proposed solution is correct.