Difference between revisions of "Aufgaben:Exercise 3.7: Angular Modulation of a Harmonic Oscillation"
m |
m (→Solution) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Frequency_Modulation_(FM) |
}} | }} | ||
| Line 56: | Line 56: | ||
|type="[]"} | |type="[]"} | ||
+ The phase deviation is $ϕ_{\rm max} = 3$. | + The phase deviation is $ϕ_{\rm max} = 3$. | ||
| − | + The | + | + The frequency deviation is $Δf_{\rm A} = 30 \ \rm kHz$. |
| − | + | + | + The instantaneous frequencies are between $0.97\ \rm MHz$ and $1.03 \ \rm MHz$ . |
- If $f_{\rm N} = 5 \ \rm kHz$ , the phase deviation would be unchanged. | - If $f_{\rm N} = 5 \ \rm kHz$ , the phase deviation would be unchanged. | ||
+ If $f_{\rm N} = 5 \ \rm kHz$ the frequency deviation would be unchanged. | + If $f_{\rm N} = 5 \ \rm kHz$ the frequency deviation would be unchanged. | ||
| Line 65: | Line 65: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' <u>Answers 1, 2 and 4</u> are correct: | '''(1)''' <u>Answers 1, 2 and 4</u> are correct: | ||
| − | *From the | + | *From the equation for $r(t)$ it can only be ascertained that it is an angle modulation, |
*but not whether it is a phase modulation (PM) or a frequency modulation (FM). | *but not whether it is a phase modulation (PM) or a frequency modulation (FM). | ||
*Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ . | *Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ . | ||
Latest revision as of 16:14, 9 April 2022
The signal arriving at a receiver is:
- $$ r(t) = 3\,{\rm V} \cdot \cos \hspace{-0.05cm} \big[2 \pi \cdot 1\,{\rm MHz} \cdot t + 3 \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\big]\hspace{0.05cm}.$$
$r(t)$ is an angle-modulated signal that was neither distorted nor influenced by noise during transmission.
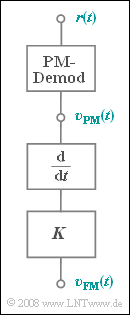
The signals $v_{\rm PM}(t)$ and $v_{\rm FM}(t)$ result after ideal demodulation by means of
- a phase demodulator, given by the equation
- $$ v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) \hspace{0.05cm},\hspace{0.3cm} {K_{\rm PM}} = 2\,{\rm V}^{-1}\hspace{0.05cm},$$
- a frequency demodulator, consisting of a PM demodulator, a differentiator and a constant $K$.
In order for all signals to have equal units, this constant $K$ is dimensionally constrained.
Hints:
- This exercise belongs to the chapter Frequency Modulation.
- Reference is also made to the chapter Phase Modulation and particularly to the section Signal characteristics with frequency modulation.
Questions
Solution
- From the equation for $r(t)$ it can only be ascertained that it is an angle modulation,
- but not whether it is a phase modulation (PM) or a frequency modulation (FM).
- Based on the equation, it is clear that the message frequency is $f_{\rm N} = 10 \ \rm kHz$ .
- The phase $ϕ_{\rm N} = 0$ of the source signal would then only apply, if phase modulation were present.
(2) With the modulator constant $K_{\rm PM} = 2 \ \rm V^{–1}$ this is given by:
- $$v_{\rm PM}(t) = \frac{1}{K_{\rm PM}} \cdot \phi_r(t) = \frac{3}{2\,{\rm V}^{-1}} \cdot \cos(2 \pi \cdot 10\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
- At time $t = 0$ it therefore holds that:
- $$v_{\rm PM}(t = 0) = {A_{\rm N}} \hspace{0.15cm}\underline {= 1.5\,{\rm V}}\hspace{0.05cm}.$$
(3) The output signal $v_{\rm FM}(t)$ of the FM demodulator – consisting of a PM–demodulator and differentiator – can be written as:
- $$v_{\rm FM}(t) = \frac{{\rm d}v_{\rm PM}(t)}{{\rm d}t} \cdot K = \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot (- \sin(2 \pi \cdot {f_{\rm N}} \cdot t))= \frac{K \cdot A_{\rm N}}{2 \pi \cdot f_{\rm N}} \cdot \cos(2 \pi \cdot {f_{\rm N}} \cdot t + 90^\circ)\hspace{0.05cm}.$$
- The message phase is thus $ϕ_{\rm N} \hspace{0.15cm}\underline {= 90^\circ}$.
(4) In this case, it must hold that:
- $$ K ={2 \pi \cdot f_{\rm N}} \hspace{0.15cm}\underline { = 6.28 \cdot 10^{4} \,\,{1}/{ s}} \hspace{0.05cm}.$$
(5) Answers 1, 2, 3 and 5 are correct:
- The phase deviation is identical to the modulation index, which can be discerned from the equation given:
- $$\phi_{\rm max} = \eta = 3 = \frac{\Delta f_{\rm A}}{ f_{\rm N}} \hspace{0.05cm}.$$
- This leads to the frequency deviation $Δf_{\rm A} = 3 · f_{\rm N} = 30 \ \rm kHz$.
- With a carrier frequency of $f_{\rm T} = 1 \ \rm MHz$ , the instantaneous frequency $f_{\rm T}(t)$ can only take values between $1±0.03 \ \rm MHz$ .
Thus, the following statement is also valid::
At half the message frequency, the phase deviation $η$ doubles, while the frequency deviation $Δf_{\rm A}$ is unaffected:
- $$\eta = \frac{K_{\rm PM} \cdot A_{\rm N}}{ f_{\rm N}} = 6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} = \eta \cdot f_{\rm N} = 6 \cdot 5\,{\rm kHz} = 30\,{\rm kHz}\hspace{0.05cm}.$$