Difference between revisions of "Aufgaben:Exercise 4.4: About the Quantization Noise"
| (12 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Modulation_Methods/Pulse_Code_Modulation |
}} | }} | ||
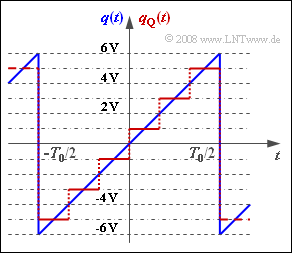
| − | [[File:P_ID1616__Mod_A_4_4.png|right|frame| | + | [[File:P_ID1616__Mod_A_4_4.png|right|frame|Quantization error with sawtooth input]] |
| − | + | To calculate the quantization noise power $P_{\rm Q}$ we assume a periodic sawtooth-shaped source signal $q(t)$ with value range $±q_{\rm max}$ and period duration $T_0$ . | |
| − | * | + | *In the mean time domain $-T_0/2 ≤ t ≤ T_0/2$ holds: $q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$ |
| − | * | + | *We refer to the power of the signal $q(t)$ here as the transmit power $P_{\rm S}$. |
| − | + | The signal $q(t)$ is quantized according to the graph with $M = 6$ steps. The quantized signal is $q_{\rm Q}(t)$, where: | |
| − | * | + | *The linear quantizer is designed for the amplitude range $±Q_{\rm max}$ such that each quantization interval has width ${\it Δ} = 2/M \cdot Q_{\rm max}$. |
| − | * | + | *The diagram shows this fact for $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$. These numerical values shall be assumed up to and including the subtask '''(5)'''. |
| − | + | The "quantization noise power" is defined as the second moment of the difference signal $ε(t) = q_{\rm Q}(t) - q(t)$. It holds: | |
:$$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ | :$$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$ | ||
| − | + | where the time $T_0'$ is to be chosen appropriately. The "quantization SNR" is the ratio $\rho_{\rm Q} = {P_{\rm S}}/{P_{\rm Q}}\hspace{0.05cm}$, which is usually given logarithmically (in dB). | |
| − | |||
| Line 24: | Line 23: | ||
| − | + | ||
| − | * | + | |
| − | * | + | Hints: |
| + | *The exercise belongs to the chapter [[Modulation_Methods/Pulse_Code_Modulation|"Pulse Code Modulation"]]. | ||
| + | *Reference is made in particular to the page [[Modulation_Methods/Pulse_Code_Modulation#Quantization_and_quantization_noise|"Quantization and quantization Noise"]]. | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the signal power $P_{\rm S}$ $($referred to the resistor $1 \ \rm Ω)$. |
|type="{}"} | |type="{}"} | ||
| − | $P_{\rm S} \ = \ $ | + | $P_{\rm S} \ = \ $ { 12 3% } $\ \rm V^2$ |
| − | { | + | {Which statements are true for the error signal $ε(t)= q_{\rm Q}(t)-q(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $ε(t)$ | + | + $ε(t)$ has a sawtooth shape. |
| − | - $ε(t)$ | + | - $ε(t)$ has a step-like progression. |
| − | + $ε(t)$ | + | + $ε(t)$ is restricted to the range $±{\it Δ}/2 = ±1 \ \rm V$. |
| − | + $ε(t)$ | + | + $ε(t)$ has period $T_0' = T_0/M$. |
| − | { | + | {What is the quantization noise power $P_{\rm Q}$ for $M=6$? |
|type="{}"} | |type="{}"} | ||
| − | $P_{\rm Q} \ = \ $ { 0.333 3% | + | $P_{\rm Q} \ = \ $ { 0.333 3% } $\ \rm V^2$ |
| − | { | + | {Calculate the quantization noise ratio for $M = 6$. |
|type="{}"} | |type="{}"} | ||
| − | $10 | + | $10 \cdot \lg \ ρ_{\rm Q} \ = \ $ { 15.56 3% } $\ \rm dB$ |
| − | { | + | {What values result from quantization with $N = 8$ or $N = 16$ bits? |
|type="{}"} | |type="{}"} | ||
| − | $N = 8\text{:}\hspace{0.35cm}10 | + | $N = 8\text{:}\hspace{0.35cm}10 ⋅ \lg \ ρ_{\rm Q} \ = \ $ { 48.16 3% } $\ \rm dB$ |
| − | $N = 16\text{:}\hspace{0.15cm}10 | + | $N = 16\text{:}\hspace{0.15cm}10 ⋅ \lg \ ρ_{\rm Q} \ = \ ${ 96.32 3% } $\ \rm dB$ |
| − | { | + | {What conditions must be met for the derived equation to apply to $ρ_{\rm Q}$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + All amplitude values are equally probable. |
| − | + | + | + A linear quantizer is present. |
| − | + | + | + The quantizer is exactly matched to the signal $(Q_{\rm max} = q_{\rm max})$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The signal power $P_{\rm S} $ is equal to the second moment of $q(t)$ if the reference resistance $1 \rm Ω$ is used and therefore the unit $\rm V^2$ is accepted for the power. |
| − | :$$P_{\rm S} | + | *Due to periodicity and symmetry, averaging over the time domain $T_0/2$ is sufficient: |
| − | + | :$$P_{\rm S} = \frac{1}{T_0/2} \cdot \int_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t= \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$ | |
| + | *Here the substitution $x = 2 - t/T_0$ was used. With $q_{\rm max} = 6 \ \rm V$ one gets $P_\rm S\hspace{0.15cm}\underline { = 12 \ V^2}$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
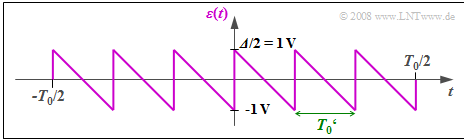
| + | [[File:Mod_A_4_4b_neu.png|right|frame|Error signal for $Q_{\rm max} = q_{\rm max}$]] | ||
| + | '''(2)''' Correct are <u>suggested solutions 1, 3, and 4</u>: | ||
| + | *We assume here $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$. | ||
| + | *This gives the sawtooth-shaped error signal $ε(t)$ between $±1\ \rm V$. | ||
| + | *The period duration is $T_0' = T_0/6$. | ||
| − | '''(3)''' | + | |
| + | '''(3)''' The error signal $ε(t)$ proceeds in the same way as $q(t)$ sawtooth. | ||
| + | *Thus, the same equation as in subtask '''(1)''' is suitable for calculating the power. | ||
| + | *Note, however, that the amplitude is smaller by a factor $M$ while the different period duration does not matter for the averaging: | ||
:$$P_{\rm Q} = \frac{P_{\rm S}}{M^2} = \frac{12\,{\rm V}^2}{36}\hspace{0.15cm}\underline {= 0.333\,{\rm V}^2 }\hspace{0.05cm}.$$ | :$$P_{\rm Q} = \frac{P_{\rm S}}{M^2} = \frac{12\,{\rm V}^2}{36}\hspace{0.15cm}\underline {= 0.333\,{\rm V}^2 }\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| + | |||
| + | '''(4)''' The results of the subtasks '''(1)''' and '''(3)''' lead to the quantization SNR: | ||
:$$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}} = M^2 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q}\hspace{0.15cm}\underline { =15.56\,{\rm dB}} \hspace{0.05cm}.$$ | :$$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}} = M^2 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q}\hspace{0.15cm}\underline { =15.56\,{\rm dB}} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | |
| − | :$$ \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\ | + | |
| − | + | '''(5)''' With $M = 2^N$ we obtain in general: | |
| + | :$$ \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} =20 \cdot {\rm lg}\hspace{0.1cm}(2)\cdot N \approx 6.02\,{\rm dB} \cdot N .$$ | ||
| + | *This results in the special cases we are looking for: | ||
:$$N = 8:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline {= 48.16\,{\rm dB}}\hspace{0.05cm},$$ | :$$N = 8:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline {= 48.16\,{\rm dB}}\hspace{0.05cm},$$ | ||
:$$N = 16:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline { = 96.32\,{\rm dB}}\hspace{0.05cm}.$$ | :$$N = 16:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline { = 96.32\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
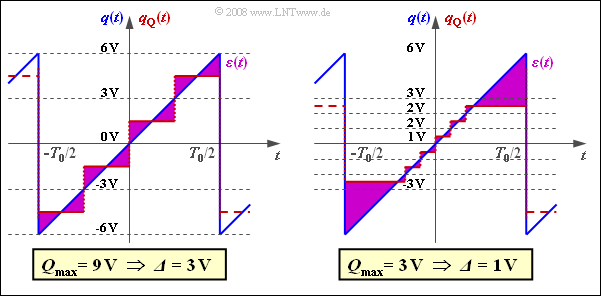
| − | [[File:P_ID1618__Mod_A_4_4f.png| | + | [[File:P_ID1618__Mod_A_4_4f.png|right|frame|Quantization with $Q_{\rm max} \ne q_{\rm max}$]] |
| + | '''(6)''' <u>All of the above preconditions</u> must be satisfied: | ||
| + | *For non-linear quantization, the simple relation $ρ_{\rm Q} = M^2$ does not hold. | ||
| + | *For an PDF other than the uniform distribution $ρ_{\rm Q} = M^2$ is also only an approximation, but this is usually accepted. | ||
| + | *If $Q_{\rm max} < q_{\rm max}$, truncation of the peaks occurs, while with $Q_{\rm max} > q_{\rm max}$ the quantization intervals are larger than required. | ||
| + | |||
| + | |||
| + | The graph shows the error signals $ε(t)$ | ||
| + | #for $Q_{\rm max} > q_{\rm max}$ (left) | ||
| + | #and $Q_{\rm max} < q_{\rm max}$ (right): | ||
| + | |||
| − | + | :In both cases, the quantization noise power is significantly larger than calculated in sub-task '''(3)'''. | |
| Line 111: | Line 126: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.1 Pulse Code Modulation^]] |
Latest revision as of 14:57, 11 April 2022
To calculate the quantization noise power $P_{\rm Q}$ we assume a periodic sawtooth-shaped source signal $q(t)$ with value range $±q_{\rm max}$ and period duration $T_0$ .
- In the mean time domain $-T_0/2 ≤ t ≤ T_0/2$ holds: $q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$
- We refer to the power of the signal $q(t)$ here as the transmit power $P_{\rm S}$.
The signal $q(t)$ is quantized according to the graph with $M = 6$ steps. The quantized signal is $q_{\rm Q}(t)$, where:
- The linear quantizer is designed for the amplitude range $±Q_{\rm max}$ such that each quantization interval has width ${\it Δ} = 2/M \cdot Q_{\rm max}$.
- The diagram shows this fact for $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$. These numerical values shall be assumed up to and including the subtask (5).
The "quantization noise power" is defined as the second moment of the difference signal $ε(t) = q_{\rm Q}(t) - q(t)$. It holds:
- $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$
where the time $T_0'$ is to be chosen appropriately. The "quantization SNR" is the ratio $\rho_{\rm Q} = {P_{\rm S}}/{P_{\rm Q}}\hspace{0.05cm}$, which is usually given logarithmically (in dB).
Hints:
- The exercise belongs to the chapter "Pulse Code Modulation".
- Reference is made in particular to the page "Quantization and quantization Noise".
Questions
Solution
- Due to periodicity and symmetry, averaging over the time domain $T_0/2$ is sufficient:
- $$P_{\rm S} = \frac{1}{T_0/2} \cdot \int_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t= \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$
- Here the substitution $x = 2 - t/T_0$ was used. With $q_{\rm max} = 6 \ \rm V$ one gets $P_\rm S\hspace{0.15cm}\underline { = 12 \ V^2}$.
(2) Correct are suggested solutions 1, 3, and 4:
- We assume here $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$.
- This gives the sawtooth-shaped error signal $ε(t)$ between $±1\ \rm V$.
- The period duration is $T_0' = T_0/6$.
(3) The error signal $ε(t)$ proceeds in the same way as $q(t)$ sawtooth.
- Thus, the same equation as in subtask (1) is suitable for calculating the power.
- Note, however, that the amplitude is smaller by a factor $M$ while the different period duration does not matter for the averaging:
- $$P_{\rm Q} = \frac{P_{\rm S}}{M^2} = \frac{12\,{\rm V}^2}{36}\hspace{0.15cm}\underline {= 0.333\,{\rm V}^2 }\hspace{0.05cm}.$$
(4) The results of the subtasks (1) and (3) lead to the quantization SNR:
- $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}} = M^2 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q}\hspace{0.15cm}\underline { =15.56\,{\rm dB}} \hspace{0.05cm}.$$
(5) With $M = 2^N$ we obtain in general:
- $$ \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} =20 \cdot {\rm lg}\hspace{0.1cm}(2)\cdot N \approx 6.02\,{\rm dB} \cdot N .$$
- This results in the special cases we are looking for:
- $$N = 8:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline {= 48.16\,{\rm dB}}\hspace{0.05cm},$$
- $$N = 16:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline { = 96.32\,{\rm dB}}\hspace{0.05cm}.$$
(6) All of the above preconditions must be satisfied:
- For non-linear quantization, the simple relation $ρ_{\rm Q} = M^2$ does not hold.
- For an PDF other than the uniform distribution $ρ_{\rm Q} = M^2$ is also only an approximation, but this is usually accepted.
- If $Q_{\rm max} < q_{\rm max}$, truncation of the peaks occurs, while with $Q_{\rm max} > q_{\rm max}$ the quantization intervals are larger than required.
The graph shows the error signals $ε(t)$
- for $Q_{\rm max} > q_{\rm max}$ (left)
- and $Q_{\rm max} < q_{\rm max}$ (right):
- In both cases, the quantization noise power is significantly larger than calculated in sub-task (3).