Difference between revisions of "Aufgaben:Exercise 4.15Z: MSK Basic Pulse and MSK Spectrum"
From LNTwww
m (Text replacement - "[[Signaldarstellung/" to "[[Signal_Representation/") |
|||
| (14 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
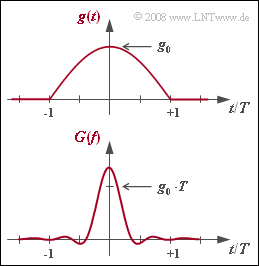
| − | [[File:P_ID1744__Mod_Z_4_14.png|right|frame|MSK | + | [[File:P_ID1744__Mod_Z_4_14.png|right|frame|MSK basic pulse and its spectrum]] |
| − | + | The fundamental pulse that is always required to [[Modulation_Methods/Nonlinear_Digital_Modulation#Realizing_MSK_as_Offset.E2.80.93QPSK|realize MSK as Offset–QPSK]] has the form shown in the graph above: | |
| − | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm | + | :$$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
| − | + | The spectral function $G(f)$ is drawn below, that is, the [[Signal_Representation/Fourier_Transform_and_its_Inverse#The_first_Fourier_integral|Fourier transform]] of $g(t)$. | |
| − | + | The corresponding equation is to be determined in this task, by considering: | |
:$$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$ | :$$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$ | ||
| − | + | The following abbreviations are used here: | |
| − | * $c(t)$ | + | * $c(t)$ is a cosine oscillation with amplitude $1$ and frequency $f_0$ (yet to be determined). |
| − | * $r(t)$ | + | * $r(t)$ is a square wave function with amplitude $g_0$ and duration $2T$. |
| Line 21: | Line 21: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Modulation_Methods/Nonlinear_Digital_Modulation|Nonlinear Digital Modulation]]. |
| − | * | + | *Particular reference is made to the page [[Modulation_Methods/Nonlinear_Digital_Modulation#Realizing_MSK_as_Offset.E2.80.93QPSK|Realizing MSK as Offset–QPSK]]. |
| − | * | + | *The result obtained here is also used in [[Aufgaben:Exercise_4.15:_MSK_Compared_with_BPSK_and_QPSK|Exercise 4.15]] . |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {How should one choose the frequency $f_0$ of the cosine oscillation $c(t)$ so that $g(t) = c(t) · r(t)$ ? |
|type="{}"} | |type="{}"} | ||
$f_0 \ = \ $ { 0.25 3% } $\ \cdot 1/T$ | $f_0 \ = \ $ { 0.25 3% } $\ \cdot 1/T$ | ||
| − | { | + | {What is the spectrum $R(f)$ of the rectangular function $r(t)$? What spectral value occurs when $f = 0$ ? |
|type="{}"} | |type="{}"} | ||
$R(f=0) \ = \ $ { 2 3% } $\ \cdot g_0 \cdot T$ | $R(f=0) \ = \ $ { 2 3% } $\ \cdot g_0 \cdot T$ | ||
| − | { | + | {Calculate the spectrun $G(f)$ of the MSK pulse $g(t)$, particularly the spectral value at $f = 0$. |
|type="{}"} | |type="{}"} | ||
$G(f=0) \ = \ $ { 1.273 3% } $\ \cdot g_0 \cdot T$ | $G(f=0) \ = \ $ { 1.273 3% } $\ \cdot g_0 \cdot T$ | ||
| − | { | + | {Summarize the result of question '''(3)''' in one term. At what frequency $f_1$ does $G(f)$ have its first zero? |
|type="{}"} | |type="{}"} | ||
$f_1 \ = \ $ { 0.75 3% } $\ \cdot 1/T$ | $f_1 \ = \ $ { 0.75 3% } $\ \cdot 1/T$ | ||
| Line 49: | Line 49: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The period of the cosine signal must be $T_0 = 4T$ . Thus, the frequency is $f_0 = 1/T_0\hspace{0.15cm}\underline {= 0.25} · 1/T$. |
| − | '''(2)''' | + | '''(2)''' The spectral function of a rectangular pulse of height $g_0$ and duration $ 2T$ is: |
:$$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} | :$$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' When $g(t) = c(t) · r(t)$ , it follows from the convolution theorem that: $ G(f) = C(f) \star R(f)\hspace{0.05cm}.$ |
| − | * | + | *The spectral function $C(f)$ consists of two Dirac functions at $± f_0$, each with weight $1/2$. From this follows: |
:$$ G(f) = 2 \cdot g_0 \cdot T \cdot \big [ 1/2 \cdot \delta (f - f_0 ) + 1/2 \cdot \delta (f + f_0 )\big ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \big ] \hspace{0.05cm}.$$ | :$$ G(f) = 2 \cdot g_0 \cdot T \cdot \big [ 1/2 \cdot \delta (f - f_0 ) + 1/2 \cdot \delta (f + f_0 )\big ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \big ] \hspace{0.05cm}.$$ | ||
| − | * | + | *Using the result $f_0 = 1/(4T)$ from question '''(1)''' , it further holds that: |
:$$G(f) = g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \big ]$$ | :$$G(f) = g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \big ]$$ | ||
:$$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \big [ {\rm si} ( - \pi/2 ) + {\rm si} ( +\pi/2 ) \big ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \pi/2 ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$ | :$$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \big [ {\rm si} ( - \pi/2 ) + {\rm si} ( +\pi/2 ) \big ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \pi/2 ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$ | ||
| − | '''(4)''' | + | '''(4)''' By writing out the $\rm si$–function, with $\sin (α ± π/2) = ± \cos(α)$, one gets: |
:$$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$ | :$$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$ | ||
:$$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$ | :$$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$ | ||
| − | * | + | *The zeroes of $G(f)$ are exclusively determined by the cosine function in the numerator, and are found at the frequencies $f · T = 0.25,\ 0.75,\ 1.25,$ ... |
| − | * | + | *However, the first zero at $f · T = 0.25$ is cancelled out by the simultaneously occuring zero in the denominator. Therefore: |
:$$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$ | :$$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$ | ||
| Line 80: | Line 80: | ||
| − | [[Category: | + | [[Category:Modulation Methods: Exercises|^4.4 Non-linear Digital Modulation^]] |
Latest revision as of 10:50, 12 April 2022
The fundamental pulse that is always required to realize MSK as Offset–QPSK has the form shown in the graph above:
- $$g_{\rm MSK}(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} | t | \le T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
The spectral function $G(f)$ is drawn below, that is, the Fourier transform of $g(t)$.
The corresponding equation is to be determined in this task, by considering:
- $$g(t) = c(t) \cdot r(t)\hspace{0.05cm}.$$
The following abbreviations are used here:
- $c(t)$ is a cosine oscillation with amplitude $1$ and frequency $f_0$ (yet to be determined).
- $r(t)$ is a square wave function with amplitude $g_0$ and duration $2T$.
Hints:
- This exercise belongs to the chapter Nonlinear Digital Modulation.
- Particular reference is made to the page Realizing MSK as Offset–QPSK.
- The result obtained here is also used in Exercise 4.15 .
Questions
Solution
(1) The period of the cosine signal must be $T_0 = 4T$ . Thus, the frequency is $f_0 = 1/T_0\hspace{0.15cm}\underline {= 0.25} · 1/T$.
(2) The spectral function of a rectangular pulse of height $g_0$ and duration $ 2T$ is:
- $$R(f) = g_0 \cdot 2 T \cdot {\rm si} ( \pi f \cdot 2T )\hspace{0.2cm}{\rm mit}\hspace{0.2cm}{\rm si} (x) = \sin(x)/x \hspace{0.3cm} \Rightarrow \hspace{0.3cm}R(f = 0) \hspace{0.15cm}\underline {= 2} \cdot g_0 \cdot T\hspace{0.05cm}.$$
(3) When $g(t) = c(t) · r(t)$ , it follows from the convolution theorem that: $ G(f) = C(f) \star R(f)\hspace{0.05cm}.$
- The spectral function $C(f)$ consists of two Dirac functions at $± f_0$, each with weight $1/2$. From this follows:
- $$ G(f) = 2 \cdot g_0 \cdot T \cdot \big [ 1/2 \cdot \delta (f - f_0 ) + 1/2 \cdot \delta (f + f_0 )\big ] \star {\rm si} ( 2 \pi f T )= g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi T \cdot (f - f_0 ) ) + {\rm si} ( 2 \pi T \cdot (f + f_0 ) ) \big ] \hspace{0.05cm}.$$
- Using the result $f_0 = 1/(4T)$ from question (1) , it further holds that:
- $$G(f) = g_0 \cdot T \cdot \big [ {\rm si} ( 2 \pi f T - \pi / 2 ) + {\rm si} ( 2 \pi f T + \pi / 2) \big ]$$
- $$\Rightarrow \hspace{0.3cm} G(f = 0) = g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \big [ {\rm si} ( - \pi/2 ) + {\rm si} ( +\pi/2 ) \big ] = 2 \cdot g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} {\rm si} ( \pi/2 ) = 2 \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{-0.02cm}\cdot\hspace{-0.02cm} \frac {{\rm sin}({\pi}/{2}) } { {\pi}/{2} } ={4}/{\pi} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T \hspace{0.15cm}\underline {\approx 1.273} \hspace{-0.02cm}\cdot\hspace{-0.02cm} g_0 \hspace{-0.02cm}\cdot\hspace{-0.02cm} T .$$
(4) By writing out the $\rm si$–function, with $\sin (α ± π/2) = ± \cos(α)$, one gets:
- $$G(f) = g_0 \cdot T \cdot \left [ \frac{{\rm sin} ( 2 \pi f T - \pi / 2 )}{2 \pi f T - \pi / 2 } + \frac{{\rm sin} ( 2 \pi f T + \pi / 2 )}{2 \pi f T + \pi / 2 } \right ]= g_0 \cdot T \cdot \frac {2}{\pi}\cdot\left [ \frac{-{\rm cos} ( 2 \pi f T )}{4 f T - 1 } + \frac{{\rm cos} ( 2 \pi f T )}{4 f T + 1 } \right ]$$
- $$\Rightarrow \hspace{0.3cm} G(f) = g_0 \cdot T \cdot \frac {2}{\pi}\cdot \frac{(1+4 f T ) \cdot {\rm cos} ( 2 \pi f T )+ (1-4 f T ) \cdot {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 } = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$
- The zeroes of $G(f)$ are exclusively determined by the cosine function in the numerator, and are found at the frequencies $f · T = 0.25,\ 0.75,\ 1.25,$ ...
- However, the first zero at $f · T = 0.25$ is cancelled out by the simultaneously occuring zero in the denominator. Therefore:
- $$f_1 \hspace{0.15cm}\underline {= 0.75} \cdot 1/T \hspace{0.05cm}.$$