Difference between revisions of "Aufgaben:Exercise 1.1Z: Non-redundant Binary Source"
| (31 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System |
}} | }} | ||
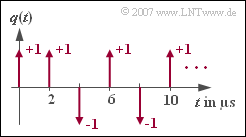
| + | [[File:P_ID1257__Dig_Z_1_1.png|right|frame|Dirac-shaped source signal]] | ||
| + | Any digital source can be completely described by its source symbol sequence | ||
| + | :$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle.$$ | ||
| + | Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source. | ||
| + | Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal | ||
| + | :$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T),$$ | ||
| + | which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients. | ||
| + | *In the case of a binary unipolar digital signal transmission holds: | ||
| + | :$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| + | *Correspondingly, in the case of a bipolar system: | ||
| + | :$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ | ||
| − | + | The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems. | |
| − | |||
| − | $$ | ||
| − | |||
| − | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System|"System Components of a Baseband Transmission System"]]. | ||
| + | *Reference is made in particular to the section [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System#Descriptive_variables_of_the_digital_source|"Descriptive variables of the digital source"]]. | ||
| + | *In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$. | ||
| + | *To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial. | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| + | {What is the symbol distance $T$? | ||
| + | |type="{}"} | ||
| + | $T \ = \ $ { 2 3% } $\ \rm µ s$ | ||
| − | { | + | {What is the bit rate $R$ output by the source? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $R \ = \ $ { 500 3% } $\ \rm kbit/s$ |
| + | |||
| + | {Is this representation unipolar or bipolar? | ||
| + | |type="()"} | ||
| + | - The symbol sequence is unipolar. | ||
| + | + The symbol sequence is bipolar. | ||
| − | { | + | {What is the source symbol $q_2$? |
| − | |type=" | + | |type="()"} |
| − | - | + | + $q_2 = \rm L$, |
| − | + | - $q_2 = \rm H$. | |
| + | {What is the symbol probability $p_{\rm H} = {\rm Pr}(q_\nu = \rm H$)? | ||
| + | |type="{}"} | ||
| + | $p_{\rm H} \ = \ $ { 0.5 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' According to the diagram, the distance between two symbols is $\underline{T = 2\ \rm µ s}$. |
| − | '''(2)''' | + | |
| − | '''(3)''' | + | |
| − | '''(4)''' | + | '''(2)''' With this redundancy-free binary source – and only with such a source – the bit rate is $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$. |
| − | '''(5)''' | + | |
| − | + | ||
| + | '''(3)''' The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is <u>bipolar</u>. | ||
| + | |||
| + | |||
| + | '''(4)''' The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$. | ||
| + | |||
| + | |||
| + | '''(5)''' Even if the diagram suggests otherwise for the short time interval shown here: For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 38: | Line 76: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.1 Baseband System Components^]] |
Latest revision as of 12:45, 29 April 2022
Any digital source can be completely described by its source symbol sequence
- $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle.$$
Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source.
Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal
- $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T),$$
which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients.
- In the case of a binary unipolar digital signal transmission holds:
- $$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
- Correspondingly, in the case of a bipolar system:
- $$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems.
Notes:
- The exercise belongs to the chapter "System Components of a Baseband Transmission System".
- Reference is made in particular to the section "Descriptive variables of the digital source".
- In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$.
- To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial.
Questions
Solution
(2) With this redundancy-free binary source – and only with such a source – the bit rate is $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$.
(3) The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is bipolar.
(4) The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$.
(5) Even if the diagram suggests otherwise for the short time interval shown here: For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold.