Difference between revisions of "Aufgaben:Exercise 1.1Z: Non-redundant Binary Source"
| (2 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System | {{quiz-Header|Buchseite=Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System | ||
}} | }} | ||
| − | |||
| − | |||
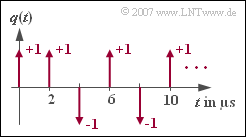
[[File:P_ID1257__Dig_Z_1_1.png|right|frame|Dirac-shaped source signal]] | [[File:P_ID1257__Dig_Z_1_1.png|right|frame|Dirac-shaped source signal]] | ||
Any digital source can be completely described by its source symbol sequence | Any digital source can be completely described by its source symbol sequence | ||
| − | :$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle$$ | + | :$$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle.$$ |
| − | Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source. | + | Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source. |
Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal | Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal | ||
| − | :$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T)$$ | + | :$$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T),$$ |
| − | which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients. | + | which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients. |
| − | *In the case of a binary unipolar digital signal transmission | + | *In the case of a binary unipolar digital signal transmission holds: |
| − | :$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{ | + | :$$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ |
| − | *Correspondingly, in the case of a bipolar system: | + | *Correspondingly, in the case of a bipolar system: |
| − | :$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{ | + | :$$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$ |
| − | The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems. | + | The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems. |
| Line 24: | Line 22: | ||
| − | + | Notes: | |
| − | *The exercise belongs to the chapter [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System|System Components of a Baseband Transmission System]]. | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System|"System Components of a Baseband Transmission System"]]. |
| − | *Reference is made in particular to the section [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System#Descriptive_variables_of_the_digital_source|Descriptive variables of the digital source]]. | + | *Reference is made in particular to the section [[Digital_Signal_Transmission/System_Components_of_a_Baseband_Transmission_System#Descriptive_variables_of_the_digital_source|"Descriptive variables of the digital source"]]. |
| − | + | *In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$. | |
| − | *In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$. | ||
*To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial. | *To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial. | ||
| Line 61: | Line 58: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' According to the diagram, the distance between two symbols is $\underline{T = 2\ \rm µ s}$. | + | '''(1)''' According to the diagram, the distance between two symbols is $\underline{T = 2\ \rm µ s}$. |
| Line 67: | Line 64: | ||
| − | '''(3)''' The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is <u>bipolar</u>. | + | '''(3)''' The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is <u>bipolar</u>. |
| − | '''(4)''' The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. | + | '''(4)''' The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$. |
| − | |||
| − | '''(5)''' Even if the diagram suggests otherwise for the short time interval shown here: | + | '''(5)''' Even if the diagram suggests otherwise for the short time interval shown here: For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold. |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 12:45, 29 April 2022
Any digital source can be completely described by its source symbol sequence
- $$\langle q_\nu \rangle = \langle \hspace{0.05cm}q_0 \hspace{0.05cm}, q_1 \hspace{0.05cm}, q_2 \hspace{0.05cm}, ... \hspace{0.05cm} \rangle.$$
Contrary to the theory part, here the control variable $\nu$ starts with zero. If each individual symbol $q_\nu$ originates from the symbol set $\{\rm L, \ H\}$, it is called a binary source.
Using the symbol spacing $T$, one can also characterize the source symbol sequence $\langle q_\nu \rangle$ in an equivalent way by the Dirac-shaped source signal
- $$q(t) = \sum_{(\nu)} a_\nu \cdot {\rm \delta} ( t - \nu \cdot T),$$
which rather corresponds to a system-theoretic approach. Here, we denote $a_\nu$ as the amplitude coefficients.
- In the case of a binary unipolar digital signal transmission holds:
- $$a_\nu = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
- Correspondingly, in the case of a bipolar system:
- $$a_\nu = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} q_\nu = \mathbf{H} \hspace{0.05cm}, \\ q_\nu = \mathbf{L} \hspace{0.05cm}. \\ \end{array}$$
The diagram shows the Dirac-shaped source signal $q(t)$ of a binary source. It is known from this source that it is redundancy-free. This statement is quite relevant for solving the problems.
Notes:
- The exercise belongs to the chapter "System Components of a Baseband Transmission System".
- Reference is made in particular to the section "Descriptive variables of the digital source".
- In the literature, the two possible binary symbols are usually designated as $\rm L$ and $\rm 0$.
- To avoid the somewhat confusing mapping $a_\nu = 1$ for $q_\nu =\rm 0$ and $a_\nu = 0$ for $q_\nu =\rm L$, we use the symbols $\rm L$ ("Low") and $\rm H$ ("High") in our learning tutorial.
Questions
Solution
(2) With this redundancy-free binary source – and only with such a source – the bit rate is $R = 1/T\hspace{0.15cm}\underline{=500 \ \rm kbit/s}$.
(3) The possible amplitude coefficients are $\pm 1$. Therefore, the given symbol sequence is bipolar.
(4) The amplitude coefficient $a_2$ can be read at $2T = 4 \ \rm µ s$. With bipolar mapping, it follows that $a_2 = -1$ for symbol $q_2 \hspace{0.15cm}\underline {=\rm L}$.
(5) Even if the diagram suggests otherwise for the short time interval shown here: For a redundancy-free binary source, in addition to the statistical independence of the symbols, $p_{\rm H} = p_{\rm L}\hspace{0.15cm}\underline{ = 0.5}$ (equally probable symbols) must also hold.