Difference between revisions of "Aufgaben:Exercise 1.6Z: Two Optimal Systems"
From LNTwww
| (8 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems |
}} | }} | ||
| − | [[File:P_ID1293__Dig_Z_1_6.png|right|frame| | + | [[File:P_ID1293__Dig_Z_1_6.png|right|frame|Optimal systems in time and frequency domain]] |
| − | + | Consider two binary transmission systems $\rm A$ and $\rm B$, which have the same error behavior for an AWGN channel with noise power density $N_{0}$. In both cases, the bit error probability is: | |
:$$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$ | :$$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$ | ||
| − | * | + | *System $\rm A$ uses the NRZ basic transmission pulse $g_{s}(t)$ according to the upper sketch with amplitude $s_{0} = 1 \ \rm V$ and duration $T = 0.5\ \rm µ s$. |
| − | * | + | *In contrast, system $\rm B$, which is to operate at the same bit rate as system $\rm A$, has a rectangular basic transmission pulse spectrum: |
:$$G_s(f) = \left\{ \begin{array}{c} G_0 \\ | :$$G_s(f) = \left\{ \begin{array}{c} G_0 \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm{ | + | \begin{array}{*{1}c} {\rm{for}} |
| − | \\ {\rm{ | + | \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |
|f| < f_0 \hspace{0.05cm}, \\ | |f| < f_0 \hspace{0.05cm}, \\ | ||
|f| > f_0 \hspace{0.05cm}.\\ | |f| > f_0 \hspace{0.05cm}.\\ | ||
| Line 21: | Line 21: | ||
| − | + | Notes: | |
| − | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Optimization_of_Baseband_Transmission_Systems|"Optimization of Baseband Transmission Systems"]]. | |
| − | * | ||
| − | * | + | *Here, the pulse amplitude is given in "volts", so that the average energy per bit $(E_{\rm B})$ has the unit $\rm V^{2}/Hz$. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {At what bit rate do the two systems operate? |
|type="{}"} | |type="{}"} | ||
$R \ = \ $ { 2 3% } $\ \rm Mbit/s$ | $R \ = \ $ { 2 3% } $\ \rm Mbit/s$ | ||
| − | { | + | {Calculate the energy per bit for system $\rm A$. |
|type="{}"} | |type="{}"} | ||
$E_{\rm B} \ = \ $ { 0.5 3% } $\ \cdot 10^{-6} \ \rm V^{2}/Hz$ | $E_{\rm B} \ = \ $ { 0.5 3% } $\ \cdot 10^{-6} \ \rm V^{2}/Hz$ | ||
| − | { | + | {Which statements are true for the receiver filters of systems $\rm A$ and $\rm B$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | +For system $\rm A$, $H_{\rm E}(f)$ has a sinc-shaped curve. |
| − | + | + | +For system $\rm B$, $H_{\rm E}(f)$ is an ideal rectangular low-pass filter. |
| − | -$H_{\rm E}(f)$ | + | -$H_{\rm E}(f)$ can be realized by an integrator in system $\rm B$. |
| − | { | + | {For which cutoff frequency $f_{0}$ does system $\rm B$ have the symbol duration $T$? |
|type="{}"} | |type="{}"} | ||
$f_{0} \ = \ ${ 1 3% } $\ \rm MHz$ | $f_{0} \ = \ ${ 1 3% } $\ \rm MHz$ | ||
| − | { | + | {How large should the constant height $G_{0}$ of the spectrum $\rm B$ be chosen so that the same energy per bit results as for system $\rm A$? |
|type="{}"} | |type="{}"} | ||
$G_{0} \ = \ $ { 0.5 3% } $\ \cdot 10^{-6} \ \rm V/Hz$ | $G_{0} \ = \ $ { 0.5 3% } $\ \cdot 10^{-6} \ \rm V/Hz$ | ||
| − | { | + | {Would one of the two systems be suitable even with peak limitation? |
|type="[]"} | |type="[]"} | ||
+System $\rm A$, | +System $\rm A$, | ||
| Line 63: | Line 62: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Both systems operate according to the specification with the same bit rate. |
| + | *The NRZ basic transmission pulse of system $\rm A$ has the symbol duration $T = 0.5\ \rm µ s$. | ||
| + | *This results in the bit rate $R = 1/T$ $ \underline{= 2\ \rm Mbit/s}$. | ||
| + | |||
| − | '''(2)''' | + | '''(2)''' The energy of the NRZ basic transmission pulse of system $\rm A$ is given by |
:$$E_{\rm B} = | :$$E_{\rm B} = | ||
\int_{-\infty}^{+\infty}g_s^2 (t)\,{\rm d} t = | \int_{-\infty}^{+\infty}g_s^2 (t)\,{\rm d} t = | ||
s_0^2 \cdot T = {1\,{\rm V^2}}\cdot {0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline { = 0.5 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | s_0^2 \cdot T = {1\,{\rm V^2}}\cdot {0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline { = 0.5 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | |
| − | *In | + | '''(3)''' The <u>first two statements are true</u>: |
| − | * | + | *In both cases $h_{\rm E}(t)$ must be equal in form to $g_{s}(t)$ and $H_{\rm E}(f)$ must be equal in form to $G_{s}(f)$. |
| − | * | + | *Thus, for system $\rm A$, the impulse response $h_{\rm E}(t)$ is rectangular and the frequency response $H_{\rm E}(f)$ is sinc-shaped. |
| + | *For system $\rm B$, $H_{\rm E}(f)$ is rectangular like $G_{s}(f)$ and thus the impulse response $h_{\rm E}(t)$ is an sinc-function. | ||
| + | *Statement 3 is false: An integrator has a rectangular impulse response and would be suitable for the realization of system $\rm A$, but not for system $\rm B$. | ||
| − | '''(4)''' | + | '''(4)''' For system $\rm B$ ⇒ $G_{d}(f)$ nearly coincides with $G_{s}(f)$. |
| + | *There is only a difference in the Nyquist frequency, but this does not affect the considerations here: | ||
| + | *While $G_{s}(f_{\rm Nyq}) = 1/2$, $G_{d}(f_{\rm Nyq}) = 1/4$. | ||
| − | + | *This results in a Nyquist system with rolloff factor $r = 0$. | |
| + | *From this follows for the Nyquist frequency from the condition that the symbol duration should also be $T = 0.5\ \rm µ s$: | ||
:$$f_{\rm 0} = f_{\rm Nyq} = \frac{1 } {2 \cdot T} = \frac{1 } {2 \cdot 0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline {= 1\,{\rm MHz}}\hspace{0.05cm}.$$ | :$$f_{\rm 0} = f_{\rm Nyq} = \frac{1 } {2 \cdot T} = \frac{1 } {2 \cdot 0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline {= 1\,{\rm MHz}}\hspace{0.05cm}.$$ | ||
| − | + | ||
| − | '''(5)''' | + | |
| + | '''(5)''' For the energy of the basic transmission pulse can also be written: | ||
:$$E_{\rm B} = | :$$E_{\rm B} = | ||
\int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = G_0^2 | \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = G_0^2 | ||
\cdot 2 f_0\hspace{0.05cm}.$$ | \cdot 2 f_0\hspace{0.05cm}.$$ | ||
| − | + | *Using the results from '''(2)''' and '''(4)''', it follows: | |
:$$G_0^2 = \frac{E_{\rm B}}{2 f_0} = \frac{5 \cdot 10^{-7}\,{\rm V^2/Hz}}{2 \cdot 10^{6}\,{\rm | :$$G_0^2 = \frac{E_{\rm B}}{2 f_0} = \frac{5 \cdot 10^{-7}\,{\rm V^2/Hz}}{2 \cdot 10^{6}\,{\rm | ||
Hz}}= 2.5 \cdot 10^{-13}\,{\rm V^2/Hz^2} | Hz}}= 2.5 \cdot 10^{-13}\,{\rm V^2/Hz^2} | ||
| Line 94: | Line 102: | ||
| − | '''(6)''' | + | '''(6)''' <u>Solution 1</u> is correct: |
| − | * | + | *System $\rm A$ represents the optimal system even with peak limitation. |
| − | * | + | *On the other hand, system $\rm B$ would be unsuitable due to the extremely unfavorable crest factor. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 102: | Line 110: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^1.4 Optimization of Baseband Systems^]] |
Latest revision as of 10:24, 4 May 2022
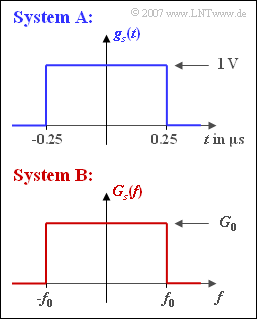
Consider two binary transmission systems $\rm A$ and $\rm B$, which have the same error behavior for an AWGN channel with noise power density $N_{0}$. In both cases, the bit error probability is:
- $$p_{\rm B} = {\rm Q} \left( \sqrt{{2 \cdot E_{\rm B}}/{N_0}}\right)\hspace{0.05cm}.$$
- System $\rm A$ uses the NRZ basic transmission pulse $g_{s}(t)$ according to the upper sketch with amplitude $s_{0} = 1 \ \rm V$ and duration $T = 0.5\ \rm µ s$.
- In contrast, system $\rm B$, which is to operate at the same bit rate as system $\rm A$, has a rectangular basic transmission pulse spectrum:
- $$G_s(f) = \left\{ \begin{array}{c} G_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} |f| < f_0 \hspace{0.05cm}, \\ |f| > f_0 \hspace{0.05cm}.\\ \end{array}$$
Notes:
- The exercise belongs to the chapter "Optimization of Baseband Transmission Systems".
- Here, the pulse amplitude is given in "volts", so that the average energy per bit $(E_{\rm B})$ has the unit $\rm V^{2}/Hz$.
Questions
Solution
(1) Both systems operate according to the specification with the same bit rate.
- The NRZ basic transmission pulse of system $\rm A$ has the symbol duration $T = 0.5\ \rm µ s$.
- This results in the bit rate $R = 1/T$ $ \underline{= 2\ \rm Mbit/s}$.
(2) The energy of the NRZ basic transmission pulse of system $\rm A$ is given by
- $$E_{\rm B} = \int_{-\infty}^{+\infty}g_s^2 (t)\,{\rm d} t = s_0^2 \cdot T = {1\,{\rm V^2}}\cdot {0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline { = 0.5 \cdot 10^{-6}\,{\rm V^2/Hz}}\hspace{0.05cm}.$$
(3) The first two statements are true:
- In both cases $h_{\rm E}(t)$ must be equal in form to $g_{s}(t)$ and $H_{\rm E}(f)$ must be equal in form to $G_{s}(f)$.
- Thus, for system $\rm A$, the impulse response $h_{\rm E}(t)$ is rectangular and the frequency response $H_{\rm E}(f)$ is sinc-shaped.
- For system $\rm B$, $H_{\rm E}(f)$ is rectangular like $G_{s}(f)$ and thus the impulse response $h_{\rm E}(t)$ is an sinc-function.
- Statement 3 is false: An integrator has a rectangular impulse response and would be suitable for the realization of system $\rm A$, but not for system $\rm B$.
(4) For system $\rm B$ ⇒ $G_{d}(f)$ nearly coincides with $G_{s}(f)$.
- There is only a difference in the Nyquist frequency, but this does not affect the considerations here:
- While $G_{s}(f_{\rm Nyq}) = 1/2$, $G_{d}(f_{\rm Nyq}) = 1/4$.
- This results in a Nyquist system with rolloff factor $r = 0$.
- From this follows for the Nyquist frequency from the condition that the symbol duration should also be $T = 0.5\ \rm µ s$:
- $$f_{\rm 0} = f_{\rm Nyq} = \frac{1 } {2 \cdot T} = \frac{1 } {2 \cdot 0.5 \cdot 10^{-6}\,{\rm s}}\hspace{0.1cm}\underline {= 1\,{\rm MHz}}\hspace{0.05cm}.$$
(5) For the energy of the basic transmission pulse can also be written:
- $$E_{\rm B} = \int_{-\infty}^{+\infty}|G_s(f)|^2 \,{\rm d} f = G_0^2 \cdot 2 f_0\hspace{0.05cm}.$$
- Using the results from (2) and (4), it follows:
- $$G_0^2 = \frac{E_{\rm B}}{2 f_0} = \frac{5 \cdot 10^{-7}\,{\rm V^2/Hz}}{2 \cdot 10^{6}\,{\rm Hz}}= 2.5 \cdot 10^{-13}\,{\rm V^2/Hz^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_0 \hspace{0.1cm}\underline {= 0.5 \cdot 10^{-6}\,{\rm V/Hz}} \hspace{0.05cm}.$$
(6) Solution 1 is correct:
- System $\rm A$ represents the optimal system even with peak limitation.
- On the other hand, system $\rm B$ would be unsuitable due to the extremely unfavorable crest factor.