Difference between revisions of "Aufgaben:Exercise 2.6: Modified MS43 Code"
| Line 60: | Line 60: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u>Statements 2 and 3</u> are correct: | + | '''(1)''' <u>Statements 2 and 3</u> are correct: |
| − | *The first statement, on the other hand, is not true: For example, the AWGN ( | + | *The first statement, on the other hand, is not true: For example, the AWGN ("Additive White Gaussian Noise") channel with a 4B3T code results in a much larger symbol error probability due to the ternary decision compared to the redundancy-free binary code. |
| − | *The $25 \%$ smaller | + | |
| + | *The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel". | ||
| + | |||
| + | *The $25 \%$ smaller baud rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency). | ||
| + | |||
| + | *For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal. | ||
| Line 68: | Line 73: | ||
'''(2)''' The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$: | '''(2)''' The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$: | ||
| − | * | + | *$\rm HHLL$ ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$, |
| − | * | + | *$\rm LHLL$ ⇒ $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$, |
| − | * | + | *$\rm LHHL$ ⇒ $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$, |
| − | * | + | *$\rm HLHL$ ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$. |
| − | Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$. | + | Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$. |
| − | '''(3)''' From the coloring of the code table, the Markov diagram can be obtained. From it, one can read the transition probabilities we are looking for: | + | '''(3)''' From the coloring of the code table, the Markov diagram can be obtained. |
| + | *From it, one can read the transition probabilities we are looking for: | ||
:$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$ | :$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$ | ||
| Line 83: | Line 89: | ||
| − | '''(4)''' <u>Statements 2 and 3</u> are correct: | + | '''(4)''' <u>Statements 2 and 3</u> are correct: |
| − | *Statement 1 is false, recognizable by the asymmetries in the Markov diagram. | + | *Statement 1 is false, recognizable by the asymmetries in the Markov diagram. |
| − | *On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$". | + | |
| − | *In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0$ we write $ {\rm Pr}(0)$ in a simplified way. | + | *On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$". |
| − | *Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram: | + | |
| + | *In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0)$ we write $ {\rm Pr}(0)$ in a simplified way. | ||
| + | |||
| + | *Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram: | ||
:$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | :$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | ||
| − | From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further: | + | *From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further: |
:$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | :$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | ||
| − | This calculation is based on the "sum of incoming arrows in state $0$". | + | :This calculation is based on the "sum of incoming arrows in state $0$". |
| − | One could also give equations for the other three states, but they all give the same result: | + | One could also give equations for the other three states, but they all give the same result: |
:$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
:$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
Revision as of 15:57, 19 May 2022
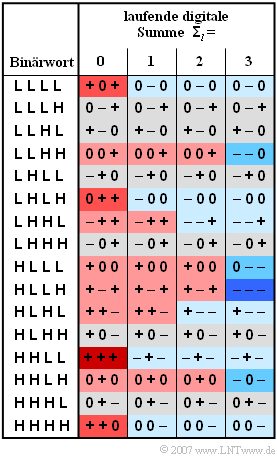
For ISDN data transmission, the MMS43 code ("Modified Monitored Sum 4B3T") is used in Germany and Belgium on the so-called $\rm {U_{K0}}$ interface, which describes the transmission path between the exchange and home. This is a 4B3T code with four code tables, which are used for coding according to the running digital sum (after $l$ blocks):
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu.$$
${\it \Sigma}_{0} = 0$ is used for initialization.
The colorings in the table mean:
- If the running digital sum does not change $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, a field is grayed out.
- An increase $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ is highlighted in red, a decrease $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ in blue.
- The more intense the coloring, the larger the change.
Notes:
- The exercise belongs to the chapter "Block Coding with 4B3T Codes".
- The binary symbols are denoted by $\rm L$ ("Low") and $\rm H$ ("High") in this learning tutorial. Often you can find the binary symbols $\rm L$ and $\rm 0$ $($instead of $\rm H)$ in the literature. Sometimes, however, $\rm L$ corresponds to our $\rm H$ and $\rm 0$ to $\rm L$.
- To avoid such confusion and to prevent the $\rm 0$ from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
- You can check the results with the (German language) SWF applet "Principle of 4B3T coding".
Questions
Solution
- The first statement, on the other hand, is not true: For example, the AWGN ("Additive White Gaussian Noise") channel with a 4B3T code results in a much larger symbol error probability due to the ternary decision compared to the redundancy-free binary code.
- The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel".
- The $25 \%$ smaller baud rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency).
- For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal.
(2) The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$:
- $\rm HHLL$ ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$,
- $\rm LHLL$ ⇒ $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$,
- $\rm LHHL$ ⇒ $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$,
- $\rm HLHL$ ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$.
Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$.
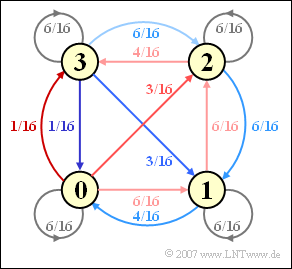
(3) From the coloring of the code table, the Markov diagram can be obtained.
- From it, one can read the transition probabilities we are looking for:
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 0)= 3/16 \ \underline{= 0.1875},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ \underline{= 0}.$$
(4) Statements 2 and 3 are correct:
- Statement 1 is false, recognizable by the asymmetries in the Markov diagram.
- On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$".
- In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0)$ we write $ {\rm Pr}(0)$ in a simplified way.
- Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram:
- $${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$
- From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further:
- $${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$
- This calculation is based on the "sum of incoming arrows in state $0$".
One could also give equations for the other three states, but they all give the same result:
- $${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$