Difference between revisions of "Aufgaben:Exercise 1.1: For Labeling Books"
From LNTwww
| (36 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Objective_of_Channel_Coding |
| − | |||
}} | }} | ||
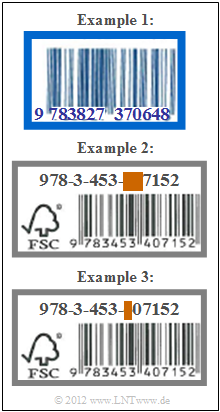
| − | [[File: | + | [[File:EN_KC_A_1_1.png|right|frame|'''ISBN–10'''? Or '''ISBN–13'''?]] |
| − | + | Since the 1960s, all books are provided with a 10-digit "International Standard Book Number" $\rm (ISBN)$. The last digit of this so-called '''ISBN-10 specification''' is calculated according to the following rule: | |
:$$ z_{10}= \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 \hspace{0.05cm}.$$ | :$$ z_{10}= \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 \hspace{0.05cm}.$$ | ||
| − | + | Since 2007, the specification according to the standard '''ISBN-13''' is additionally mandatory, whereby the check digit $z_{\rm 13}$ then results as follows: | |
:$$z_{13} = 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1)\mod 2} \right ) \hspace{-0.2cm} \mod 10 \hspace{0.05cm}.$$ | :$$z_{13} = 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1)\mod 2} \right ) \hspace{-0.2cm} \mod 10 \hspace{0.05cm}.$$ | ||
| − | |||
| − | + | Some exemplary "ISBNs" are given opposite. The following questions refer to these. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hints: This exercise belongs to the chapter [[Channel_Coding/Objective_of_Channel_Coding|"Objective of Channel Coding"]] | |
| − | | | + | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Questions=== | |
| − | |||
| − | |||
| − | + | <quiz display=simple> | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | What is the standard for $\text{Example 1}$? | ||
| + | |type="()"} | ||
| + | - ISBN-10, | ||
| + | +ISBN-13. | ||
| + | {Accordingly $\text{Example 2}$ two digits of an ISBN-13 are deleted. Is it possible to reconstruct the ISBN? If yes: Specify the ISBN-13. | ||
| + | |type="()"} | ||
| + | - Yes, | ||
| + | +No. | ||
| + | {According to $\text{Example 3}$ one digit of an ISBN-13 is erased. Can the ISBN be reconstructed? If Yes: Specify the ISBN-13. | ||
| + | |type="()"} | ||
| + | +Yes, | ||
| + | -No. | ||
| − | { | + | {How many different values $(M)$ can the check digit $z_{\rm 10}$ take for ISBN-10? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $M \ = \ $ { 11 3% } $\ \rm$ |
| + | {Assumed as ISBN-10 is "3-8273-7064-7". Which statement is true? | ||
| + | |type="()"} | ||
| + | - This is not a valid ISBN. | ||
| + | + The ISBN could be correct. | ||
| + | - The ISBN is certainly correct. | ||
| + | </quiz> | ||
| + | |||
| + | ===Solution=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' Just by counting the ISBN digits, you can tell that <u>answer 2</u> is correct. The weighted sum over all digits is a multiple of 10: | ||
| + | :$$S \ = \ \hspace{-0.1cm} \sum_{i=1}^{13} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \cdot 2} = (9+8+8+7+6+8) \cdot 1 + (7+3+2+3+0+4) \cdot 3 = 110\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} S \hspace{-0.2cm} \mod 10 \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' The answer is <u>No</u>. Only one cancellation can be reconstructed with a single check digit. | ||
| + | |||
| + | |||
| + | '''(3)''' One digit can be reconstructed ⇒ <u>Yes</u>. For the digit $z_{\rm 8}$, it must hold: | ||
| + | :$$[(9+8+4+3+0+1+2) \cdot 1 + (7+3+5+z_8+7+5) \cdot 3] \hspace{-0.2cm} \mod 10 = 0\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} [108 + 3z_8] \hspace{-0.2cm} \mod 10 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_8 \hspace{0.15cm}\underline {= 4} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' By the modulo 11 operation, $z_{10}$ can take the values $0,\ 1,\ \text{...} ,\ 10$ ⇒ $\underline{M =11}$. | ||
| + | *Since "10" is not a digit, one makes do with $z_{10} = \rm X$. | ||
| + | *This corresponds to the Roman representation of the number "10". | ||
| − | |||
| − | == | + | '''(5)''' The test condition is: |
| − | {{ | + | :$$\ \ S= \left ( \sum_{i=1}^{10} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 = 0 \hspace{0.05cm}.$$ |
| − | + | ||
| − | + | *The given ISBN satisfies this condition: | |
| − | + | :$$3 \cdot 1 + 8 \cdot 2 + 2 \cdot 3 + 7 \cdot 4 + 3 \cdot 5 + 7 \cdot 6 + 0 \cdot 7 + 6 \cdot 8 + 4 \cdot 9 + 7 \cdot 10 = 264\hspace{0.3cm} | |
| − | + | ⇒\hspace{0.3cm} S= 264 \hspace{-0.3cm} \mod 11 = 0 \hspace{0.05cm}.$$ | |
| − | + | *Correct is <u>statement 2</u>, since the check sum $S = 0$ could result even with more than one error. | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^1.1 Objective of Channel Coding^]] |
| − | |||
| − | ^]] | ||
Latest revision as of 12:53, 6 June 2022
ISBN–10? Or ISBN–13?
Since the 1960s, all books are provided with a 10-digit "International Standard Book Number" $\rm (ISBN)$. The last digit of this so-called ISBN-10 specification is calculated according to the following rule:
- $$ z_{10}= \left ( \sum_{i=1}^{9} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 \hspace{0.05cm}.$$
Since 2007, the specification according to the standard ISBN-13 is additionally mandatory, whereby the check digit $z_{\rm 13}$ then results as follows:
- $$z_{13} = 10 - \left ( \sum_{i=1}^{12} \hspace{0.2cm} z_i \cdot 3^{(i+1)\mod 2} \right ) \hspace{-0.2cm} \mod 10 \hspace{0.05cm}.$$
Some exemplary "ISBNs" are given opposite. The following questions refer to these.
Hints: This exercise belongs to the chapter "Objective of Channel Coding"
Questions
Solution
(1) Just by counting the ISBN digits, you can tell that answer 2 is correct. The weighted sum over all digits is a multiple of 10:
- $$S \ = \ \hspace{-0.1cm} \sum_{i=1}^{13} \hspace{0.2cm} z_i \cdot 3^{(i+1) \hspace{-0.2cm} \cdot 2} = (9+8+8+7+6+8) \cdot 1 + (7+3+2+3+0+4) \cdot 3 = 110\hspace{0.3cm} \Rightarrow \hspace{0.3cm} S \hspace{-0.2cm} \mod 10 \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$
(2) The answer is No. Only one cancellation can be reconstructed with a single check digit.
(3) One digit can be reconstructed ⇒ Yes. For the digit $z_{\rm 8}$, it must hold:
- $$[(9+8+4+3+0+1+2) \cdot 1 + (7+3+5+z_8+7+5) \cdot 3] \hspace{-0.2cm} \mod 10 = 0\hspace{0.3cm} \Rightarrow \hspace{0.3cm} [108 + 3z_8] \hspace{-0.2cm} \mod 10 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_8 \hspace{0.15cm}\underline {= 4} \hspace{0.05cm}.$$
(4) By the modulo 11 operation, $z_{10}$ can take the values $0,\ 1,\ \text{...} ,\ 10$ ⇒ $\underline{M =11}$.
- Since "10" is not a digit, one makes do with $z_{10} = \rm X$.
- This corresponds to the Roman representation of the number "10".
(5) The test condition is:
- $$\ \ S= \left ( \sum_{i=1}^{10} \hspace{0.2cm} i \cdot z_i \right ) \hspace{-0.2cm} \mod 11 = 0 \hspace{0.05cm}.$$
- The given ISBN satisfies this condition:
- $$3 \cdot 1 + 8 \cdot 2 + 2 \cdot 3 + 7 \cdot 4 + 3 \cdot 5 + 7 \cdot 6 + 0 \cdot 7 + 6 \cdot 8 + 4 \cdot 9 + 7 \cdot 10 = 264\hspace{0.3cm} ⇒\hspace{0.3cm} S= 264 \hspace{-0.3cm} \mod 11 = 0 \hspace{0.05cm}.$$
- Correct is statement 2, since the check sum $S = 0$ could result even with more than one error.
