Difference between revisions of "Aufgaben:Exercise 3.3: Noise at Channel Equalization"
| Line 77: | Line 77: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' From $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$ follows $\rho_{\rm U} = 10^{\rm 1.48} ≈ 30.2$ and | + | '''(1)''' From $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$ follows $\rho_{\rm U} = 10^{\rm 1.48} ≈ 30.2$ and with the given equation: |
:$$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow | :$$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} | \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} | ||
| Line 83: | Line 83: | ||
| − | '''(2)''' With the same error probability $p_{\rm U}$ (and thus the same $\rho_{\rm U}$), $\sigma_d$ must have exactly the same value as calculated in subtask '''(1)''', since the eye opening also remains the same ⇒ $\sigma_d/s_0 \underline{= 0.044}.$ | + | '''(2)''' With the same worst-case error probability $p_{\rm U}$ (and thus the same $\rho_{\rm U}$), $\sigma_d$ must have exactly the same value as calculated in subtask '''(1)''', since the eye opening also remains the same ⇒ $\sigma_d/s_0 \underline{= 0.044}.$ |
| Line 95: | Line 95: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Expressed in ${\rm dB}$, one thus obtains | + | Expressed in ${\rm dB}$, one thus obtains |
:$$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = | :$$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = | ||
-70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = | -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = | ||
| Line 101: | Line 101: | ||
| − | '''(4)''' For system $\rm B$, because $H_{\rm E}(f = 0) = 1$, the normalized value is equal to $1$, that means, it is ${\it \Phi}_{d \rm N}(f = 0) = N_0/2$. | + | '''(4)''' For system $\rm B$, because of $H_{\rm E}(f = 0) = 1$, the normalized value is equal to $1$, that means, it is ${\it \Phi}_{d \rm N}(f = 0) = N_0/2$. |
| − | In contrast, for system $\rm A$, this value is larger by $1/\alpha^2$ due to the components of the frequency-independent cable attenuation $\alpha$: | + | In contrast, for system $\rm A$, this value is larger by the factor $1/\alpha^2$ due to the components of the frequency-independent cable attenuation $\alpha$: |
:$${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, \hspace{1.05cm}{\rm System\hspace{0.15cm}B}: \frac{{\it \Phi}_{d \rm N}(f = 0)}{N_0/2} \, \underline {= 1}.$$ | :$${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, \hspace{1.05cm}{\rm System\hspace{0.15cm}B}: \frac{{\it \Phi}_{d \rm N}(f = 0)}{N_0/2} \, \underline {= 1}.$$ | ||
| − | '''(5)''' ${\it \Phi}_{d \rm N}(f)$ is maximal if the exponent | + | '''(5)''' ${\it \Phi}_{d \rm N}(f)$ is maximal if the exponent |
:$$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$ | :$$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$ | ||
| − | has the maximum value. Thus, with $x = f \cdot T$, the optimization function is: | + | has the maximum value. Thus, with $x = f \cdot T$, the optimization function is: |
:$$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot | :$$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot | ||
\sqrt{x} - 13 \cdot x^2 \hspace{0.3cm} | \sqrt{x} - 13 \cdot x^2 \hspace{0.3cm} | ||
| Line 121: | Line 121: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | This gives $f_{\rm max} \cdot T\hspace{0.15cm}\underline {\approx 0.63}$. | + | This gives $f_{\rm max} \cdot T\hspace{0.15cm}\underline {\approx 0.63}$. |
| − | '''(6)''' With $x_{\rm max} = 0.63$ we get the function value | + | '''(6)''' With $x_{\rm max} = 0.63$ we get the function value |
:$$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 | :$$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 | ||
\hspace{0.15cm}\underline {\approx 15.477}.$$ | \hspace{0.15cm}\underline {\approx 15.477}.$$ | ||
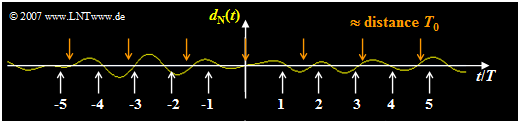
| − | [[File:EN_Dig_A_3_3f.png|frame|right|Noise component $d_{\rm N}(t)$]] | + | [[File:EN_Dig_A_3_3f.png|frame|right|Noise component $d_{\rm N}(t)$ of the detection signal]] |
It follows: | It follows: | ||
| − | *The noise | + | *The noise PSD at the (normalized) frequency $f \cdot T \approx 0.63$ is larger than at the frequency $f = 0$ by a factor of $e^{\rm 15.5} \ \underline{\approx 5.4 \cdot 10^6}$. |
| − | *Thus, periodic components with period $T_0 \approx 1.6 \cdot T$ predominate in the noise component $d_{\rm N}(t)$. | + | *Thus, periodic components with period $T_0 \approx 1.6 \cdot T$ predominate in the noise component $d_{\rm N}(t)$. |
| + | |||
*The graph shows a simulation and confirms this result. | *The graph shows a simulation and confirms this result. | ||
Latest revision as of 13:17, 17 June 2022
We consider two different system variants, both using NRZ rectangular transmission pulses and are affected by AWGN noise.
- To limit the noise power, in both cases a Gaussian low-pass filter
- $$H_{\rm G}(f) = {\rm exp}(- \pi \cdot \frac{f^2}{(2f_{\rm G})^2})$$
- with normalized cutoff frequency $f_{\rm G} \cdot T = 0.35$ is used, so that both systems also have the same eye opening with $\ddot{o}(T_{\rm D} = 0) = 0.478 \cdot s_0$.
- The transmission energy $E_{\rm B} = s_0^2 \cdot T$ spent per bit is larger than the noise power density $N_0$ by a factor of $10^9$ ⇒ $10\cdot {\rm lg} \, E_{\rm B}/N_0 = 90 \, {\rm dB}$.
- The channel frequency response of system $\rm A$ is frequency-independent: $H_{\rm K}(f) = \alpha$. Accordingly, for the receiver filter $H_{\rm E}(f) = H_{\rm G}(f)/\alpha$ must be assumed, so that the following applies to the detection noise power:
- $$\sigma_d^2 = {N_0}/{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \alpha^2} \hspace{0.05cm}.$$
- In contrast, system $\rm B$ assumes a coaxial cable with characteristic attenuation $($at half the bit rate$)$ $a_* = 80 \, {\rm dB}$ $($or $9.2 \, {\rm Np})$ so that the channel magnitude frequency response is:
- $$|H_{\rm K}(f)| = {\rm e}^{- 9.2 \hspace{0.05cm} \cdot \hspace{0.05cm}\sqrt{2 f T}}\hspace{0.05cm}.$$
- Thus, the equation for the noise power density $\rm (PSD)$ before the decision is $($with $f_{\rm G} \cdot T = 0.35)$:
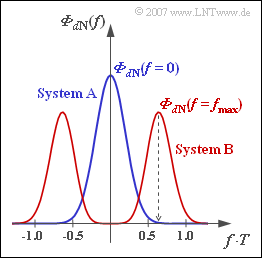
- $${\it \Phi}_{d{\rm N}}(f) = {N_0}/{2} \cdot \frac{|H_{\rm G }(f)|^2}{|H_{\rm K}(f)|^2} = {N_0}/{2} \cdot {\rm exp}\left [18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{(2 \cdot 0.35)^2} \right ] \hspace{0.05cm}.$$
- The noise PSD of system $\rm B$ is shown in red in the above graph and the noise PSD of system $\rm A$ is drawn in blue.
- For the system $\rm B$, the worst-case error probability
- $$p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right) \hspace{0.4cm}{\rm with} \hspace{0.4cm} \rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}$$
- was determined. The measurement resulted in $p_{\rm U} = 4 \cdot 10^{\rm -8}$, which corresponds to the signal-to-noise ratio $10 \cdot {\rm lg} \, \rho_{\rm U} = 14.8 \, {\rm dB}$.
Notes:
- The exercise belongs to the chapter "Consideration of Channel Distortion and Equalization".
- Use the "Complementary Gaussian Error Functions" interaction module for numerical evaluation of the Q–function.
Questions
Solution
- $$\sqrt{\rho_{\rm U}} = \frac{\ddot{o}(T_{\rm D})/2}{ \sigma_d}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma_d = \frac{0.478 \cdot s_0/2}{ \sqrt{30.2}} \hspace{0.15cm}\underline { \approx 0.044 \cdot s_0 }\hspace{0.05cm}.$$
(2) With the same worst-case error probability $p_{\rm U}$ (and thus the same $\rho_{\rm U}$), $\sigma_d$ must have exactly the same value as calculated in subtask (1), since the eye opening also remains the same ⇒ $\sigma_d/s_0 \underline{= 0.044}.$
(3) According to the specification section:
- $$\alpha^2 = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = \frac{10^{-9} \cdot s_0^2 \cdot T \cdot f_{\rm G}}{\sqrt{2} \cdot \sigma_d^2} = 10^{-9} \cdot \frac{ f_{\rm G} \cdot T}{\sqrt{2} \cdot (\sigma_d/s_0)^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \alpha^2 = 10^{-9} \cdot \frac{ 0.35}{\sqrt{2} \cdot 0.044^2} \approx 1.28 \cdot 10^{-7} \hspace{0.05cm}.$$
Expressed in ${\rm dB}$, one thus obtains
- $$20 \cdot {\rm lg}\hspace{0.1cm}\alpha = 10 \cdot {\rm lg}\hspace{0.1cm}\alpha^2 = -70\,{\rm dB}\hspace{0.1cm}+\hspace{0.1cm}10 \cdot {\rm lg}\hspace{0.1cm}1.28\hspace{0.15cm}\underline { = -68.9\,{\rm dB}} \hspace{0.05cm}.$$
(4) For system $\rm B$, because of $H_{\rm E}(f = 0) = 1$, the normalized value is equal to $1$, that means, it is ${\it \Phi}_{d \rm N}(f = 0) = N_0/2$.
In contrast, for system $\rm A$, this value is larger by the factor $1/\alpha^2$ due to the components of the frequency-independent cable attenuation $\alpha$:
- $${\rm System}\hspace{0.15cm}{\rm A:}\hspace{0.1cm}\frac{{\it \Phi}_{d{\rm N}}(f = 0)}{N_0/2} = \frac{1}{\alpha^2} \hspace{0.15cm}\underline {\approx 7.8 \cdot 10^{6}} \hspace{0.05cm}, \hspace{1.05cm}{\rm System\hspace{0.15cm}B}: \frac{{\it \Phi}_{d \rm N}(f = 0)}{N_0/2} \, \underline {= 1}.$$
(5) ${\it \Phi}_{d \rm N}(f)$ is maximal if the exponent
- $$18.4 \cdot \sqrt{2 f T} - 2\pi \cdot \frac{(f \cdot T)^2}{0.49}$$
has the maximum value. Thus, with $x = f \cdot T$, the optimization function is:
- $$y(x) = 26.022 \cdot \sqrt{x} - 12.823 \cdot x^2 \approx 26 \cdot \sqrt{x} - 13 \cdot x^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{{\rm d}y}{{\rm d}x} = \frac{26} {2\cdot \sqrt{x}} - 13 \cdot 2 \cdot x = 0$$
- $$\Rightarrow \hspace{0.3cm} \frac{1} { \sqrt{x}} = 2 \cdot x \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\frac{1} { x} = 4 \cdot x^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x^3 = 0.25 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x \approx 0.63 \hspace{0.05cm}.$$
This gives $f_{\rm max} \cdot T\hspace{0.15cm}\underline {\approx 0.63}$.
(6) With $x_{\rm max} = 0.63$ we get the function value
- $$y(x_{\rm max}) \approx 26 \cdot \sqrt{0.63} - 13 \cdot 0.63^2 \hspace{0.15cm}\underline {\approx 15.477}.$$
It follows:
- The noise PSD at the (normalized) frequency $f \cdot T \approx 0.63$ is larger than at the frequency $f = 0$ by a factor of $e^{\rm 15.5} \ \underline{\approx 5.4 \cdot 10^6}$.
- Thus, periodic components with period $T_0 \approx 1.6 \cdot T$ predominate in the noise component $d_{\rm N}(t)$.
- The graph shows a simulation and confirms this result.