Difference between revisions of "Linear and Time Invariant Systems/Inverse Laplace Transform"
| Line 19: | Line 19: | ||
*Verwendet man ein diracförmiges Eingangssignal $x(t) = δ(t) ⇒ X_{\rm L}(p) = 1 ⇒ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt das Ausgangssignal $y(t)$ die Impulsantwort $h(t)$ des kausalen Übertragungssystems. Zur Berechnung dürfen nur die grün eingezeichneten Singularitäten herangezogen werden. | *Verwendet man ein diracförmiges Eingangssignal $x(t) = δ(t) ⇒ X_{\rm L}(p) = 1 ⇒ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt das Ausgangssignal $y(t)$ die Impulsantwort $h(t)$ des kausalen Übertragungssystems. Zur Berechnung dürfen nur die grün eingezeichneten Singularitäten herangezogen werden. | ||
*Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p =$ 0 zu berücksichtigen. | *Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p =$ 0 zu berücksichtigen. | ||
| − | *Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \ | + | *Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel 3.2), zum Beispiel ein zum Zeitpunkt $t =$ 0 eingeschaltetes Cosinus– oder Sinussignal. Deren Laplace–Transformierte sind in der obigen Grafik ebenfalls angegeben. |
| + | |||
| + | |||
| + | Bei der hier beschriebenen Vorgehensweise ist ein Rechteck $x(t) ⇒ X_{\rm L}(p) = (1 – e^{pT})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden. | ||
| + | |||
| + | ==Einige Ergebnisse der Funktionentheorie== | ||
| + | Im Gegensatz zu den Fourierintegralen, die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei Laplace die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation – | ||
| + | *sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$, | ||
| + | *auf elementarem Weg nicht oder nur sehr umständlich lösbar. | ||
| + | |||
| + | |||
| + | {{Definition}} | ||
| + | Allgemein gilt für die Laplace–Rücktransformation: | ||
| + | $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{{\rm j} \cdot 2 \pi}\cdot \int\limits_{\alpha-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta}^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} { Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{p \hspace{0.05cm}t}}\hspace{0.1cm}{\rm | ||
| + | d}p \hspace{0.05cm} .$$ | ||
| + | Die Integration erfolgt parallel zur imaginären Achse (gepunktete Linie in der Grafik). Der Realteil $α$ muss dabei so gewählt werden, dass alle Pole links vom Integrationsweg liegen. | ||
| + | {{end}} | ||
| + | |||
| + | |||
| − | |||
Revision as of 18:44, 12 May 2016
Problemstellung und Voraussetzungen
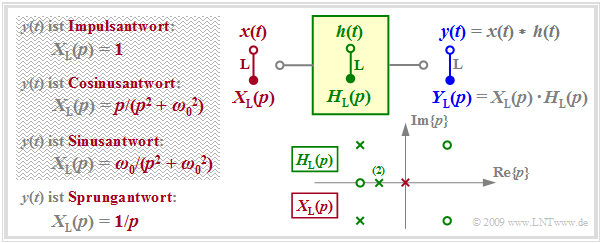
Das Kapitel 3.3 behandelt die folgende Problemstellung: Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. Gesucht ist die Laplace–Rücktransformierte, die die dazugehörige Zeitfunktion $y(t)$ angibt und die in diesem Tutorial wie folgt bezeichnet wird: $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$
In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt:
$H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem, während $Y_{\rm L}(p)$ die Laplace–Transformierte des gesuchten Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ bezeichnet. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$
- Die Pole und Nullstellen zeigen die in Kapitel 3.2 genannten Eigenschaften. Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind auch in der rechten $p$–Halbebene erlaubt.
- Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind ebenfalls erlaubt.
- Verwendet man ein diracförmiges Eingangssignal $x(t) = δ(t) ⇒ X_{\rm L}(p) = 1 ⇒ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt das Ausgangssignal $y(t)$ die Impulsantwort $h(t)$ des kausalen Übertragungssystems. Zur Berechnung dürfen nur die grün eingezeichneten Singularitäten herangezogen werden.
- Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p =$ 0 zu berücksichtigen.
- Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel 3.2), zum Beispiel ein zum Zeitpunkt $t =$ 0 eingeschaltetes Cosinus– oder Sinussignal. Deren Laplace–Transformierte sind in der obigen Grafik ebenfalls angegeben.
Bei der hier beschriebenen Vorgehensweise ist ein Rechteck $x(t) ⇒ X_{\rm L}(p) = (1 – e^{pT})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden.
Einige Ergebnisse der Funktionentheorie
Im Gegensatz zu den Fourierintegralen, die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei Laplace die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation –
- sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$,
- auf elementarem Weg nicht oder nur sehr umständlich lösbar.
Allgemein gilt für die Laplace–Rücktransformation: $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{{\rm j} \cdot 2 \pi}\cdot \int\limits_{\alpha-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta}^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} { Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{p \hspace{0.05cm}t}}\hspace{0.1cm}{\rm d}p \hspace{0.05cm} .$$ Die Integration erfolgt parallel zur imaginären Achse (gepunktete Linie in der Grafik). Der Realteil $α$ muss dabei so gewählt werden, dass alle Pole links vom Integrationsweg liegen.