Difference between revisions of "Aufgaben:Exercise 3.12: Trellis Diagram for Two Precursors"
From LNTwww
| (19 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Viterbi_Receiver}} |
| − | [[File:P_ID1478__Dig_A_3_12.png|right|frame| | + | [[File:P_ID1478__Dig_A_3_12.png|right|frame|Trellis diagram for two precursors]] |
| − | + | We assume the basic pulse values $g_0\ne 0$, $g_{\rm –1}\ne 0$ and $g_{\rm –2}\ne 0$: | |
| − | + | *This means that the decision on the symbol $a_{\rm \nu}$ is also influenced by the subsequent coefficients $a_{\rm \nu +1}$ and $a_{\rm \nu +2}$. | |
| − | + | ||
| + | *Thus, for each time point $\nu$, exactly eight '''metrics''' $\varepsilon_{\rm \nu}$ have to be determined, from which the '''minimum accumulated metrics''' ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ and ${\it \Gamma}_{\rm \nu}(11)$ can be calculated. | ||
| − | + | *For example, ${\it \Gamma}_{\rm \nu}(01)$ provides information about the symbol $a_{\rm \nu}$ under the assumption that $a_{\rm \nu +1} = 0$ and $a_{\rm \nu +2} = 1$ will be. | |
| − | * | + | |
| − | * | + | *Here, the minimum accumulated metric ${\it \Gamma}_{\rm \nu}(01)$ is the smaller value obtained from the comparison of |
| − | * | + | :$$\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001)\big] \hspace{0.15cm}{\rm and} |
| − | * | + | \hspace{0.15cm}\big[{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big].$$ |
| − | :$${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{ | + | |
| + | To calculate the minimum accumulated metric ${\it \Gamma}_2(10)$ in subtasks '''(1)''' and '''(2)''', assume the following numerical values: | ||
| + | * unipolar amplitude coefficients: $a_{\rm \nu} ∈ \{0, 1\}$, | ||
| + | |||
| + | * basic pulse values $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2$, | ||
| + | |||
| + | * applied noisy detection sample: $d_2 = 0.2$, | ||
| + | |||
| + | * minimum accumulated metric at time $\nu = 1$: | ||
| + | :$${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{0.2cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = | ||
1.2 | 1.2 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The graph shows the simplified trellis diagram for time points $\nu = 1$ to $\nu = 8$. | |
| + | *Blue branches come from either ${\it \Gamma}_{\rm \nu –1}(00)$ or ${\it \Gamma}_{\rm \nu –1}(01)$ and denote a hypothetical "$0$". | ||
| + | |||
| + | *In contrast, all red branches – starting from the ${\it \Gamma}_{\rm \nu –1}(10)$ or ${\it \Gamma}_{\rm \nu –1}(11)$ states – indicate the symbol "$1$". | ||
| + | |||
| + | |||
| − | + | Notes: | |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Viterbi_Receiver|"Viterbi Receiver"]]. |
| − | + | ||
| − | * | + | * All quantities here are to be understood normalized. |
| + | * Also, assume unipolar and equal probability amplitude coefficients: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$ | ||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the following metrics: |
| + | |type="{}"} | ||
| + | $\varepsilon_2(010) \ = \ $ { 0.01 3% } | ||
| + | $\varepsilon_2(011) \ = \ $ { 0.09 3% } | ||
| + | $\varepsilon_2(110) \ = \ $ { 0.36 3% } | ||
| + | $\varepsilon_2(111) \ = \ $ { 0.64 3% } | ||
| + | |||
| + | {Calculate the following minimum accumulated metrics: | ||
| + | |type="{}"} | ||
| + | ${\it \Gamma}_2(10) \ = \ $ { 0.21 3% } | ||
| + | ${\it \Gamma}_2(11) \ = \ $ { 0.29 3% } | ||
| + | |||
| + | {What are the symbols output by the Viterbi receiver? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | + The first seven symbols are "$1011010$". |
| − | + | + | - The first seven symbols are "$1101101$". |
| + | - The last symbol $a_8 = 1$ is safe. | ||
| + | + No definite statement can be made about the symbol $a_8$. | ||
| + | </quiz> | ||
| + | |||
| + | ===Solution=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' The first metric is calculated as follows: | ||
| + | :$$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | Correspondingly, for the other metrics: | ||
| + | :$$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$ | ||
| + | :$$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$ | ||
| + | :$$\varepsilon_{2}(111) \ = \ [0.2 -0.5- 0.3-0.2]^2\hspace{0.15cm}\underline {=0.64} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | { | + | '''(2)''' The task is to find the minimum value of each of two comparison values: |
| − | + | :$${\it \Gamma}_{2}(10) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(010), | |
| − | $\ | + | \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(110)\right] = {\rm Min}\left[0.2+ 0.01, 1.2 + 0.36\right]\hspace{0.15cm}\underline {= 0.21} |
| + | \hspace{0.05cm},$$ | ||
| + | :$${\it \Gamma}_{2}(11) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(011), | ||
| + | \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(111)\right] = {\rm Min}\left[0.2+ 0.09, 1.2 + 0.64\right]\hspace{0.15cm}\underline {= 0.29} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | '''(3)''' The <u>first and last solutions</u> are correct: | ||
| + | *The sequence "$1011010$" can be recognized from the continuous path: "red – blue – red – red – blue – red – blue". | ||
| − | + | *On the other hand, no final statement can be made about the symbol $a_8$ at time $\nu = 8$: | |
| − | === | + | *Only under the hypothesis $a_9 = 1$ <u>and</u> $a_{\rm 10} = 1$ one would decide for $a_8 = 0$, under other hypotheses for $a_8 = 1$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^3.8 Viterbi Receiver^]] |
Latest revision as of 16:34, 4 July 2022
We assume the basic pulse values $g_0\ne 0$, $g_{\rm –1}\ne 0$ and $g_{\rm –2}\ne 0$:
- This means that the decision on the symbol $a_{\rm \nu}$ is also influenced by the subsequent coefficients $a_{\rm \nu +1}$ and $a_{\rm \nu +2}$.
- Thus, for each time point $\nu$, exactly eight metrics $\varepsilon_{\rm \nu}$ have to be determined, from which the minimum accumulated metrics ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ and ${\it \Gamma}_{\rm \nu}(11)$ can be calculated.
- For example, ${\it \Gamma}_{\rm \nu}(01)$ provides information about the symbol $a_{\rm \nu}$ under the assumption that $a_{\rm \nu +1} = 0$ and $a_{\rm \nu +2} = 1$ will be.
- Here, the minimum accumulated metric ${\it \Gamma}_{\rm \nu}(01)$ is the smaller value obtained from the comparison of
- $$\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001)\big] \hspace{0.15cm}{\rm and} \hspace{0.15cm}\big[{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big].$$
To calculate the minimum accumulated metric ${\it \Gamma}_2(10)$ in subtasks (1) and (2), assume the following numerical values:
- unipolar amplitude coefficients: $a_{\rm \nu} ∈ \{0, 1\}$,
- basic pulse values $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2$,
- applied noisy detection sample: $d_2 = 0.2$,
- minimum accumulated metric at time $\nu = 1$:
- $${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{0.2cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = 1.2 \hspace{0.05cm}.$$
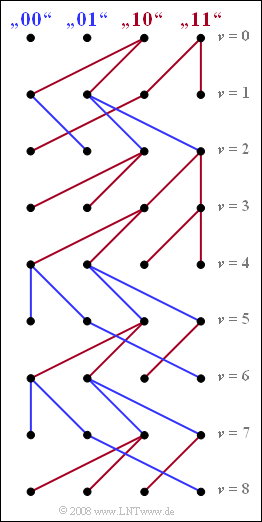
The graph shows the simplified trellis diagram for time points $\nu = 1$ to $\nu = 8$.
- Blue branches come from either ${\it \Gamma}_{\rm \nu –1}(00)$ or ${\it \Gamma}_{\rm \nu –1}(01)$ and denote a hypothetical "$0$".
- In contrast, all red branches – starting from the ${\it \Gamma}_{\rm \nu –1}(10)$ or ${\it \Gamma}_{\rm \nu –1}(11)$ states – indicate the symbol "$1$".
Notes:
- The exercise belongs to the chapter "Viterbi Receiver".
- All quantities here are to be understood normalized.
- Also, assume unipolar and equal probability amplitude coefficients: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
Questions
Solution
(1) The first metric is calculated as follows:
- $$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} \hspace{0.05cm}.$$
Correspondingly, for the other metrics:
- $$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$
- $$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$
- $$\varepsilon_{2}(111) \ = \ [0.2 -0.5- 0.3-0.2]^2\hspace{0.15cm}\underline {=0.64} \hspace{0.05cm}.$$
(2) The task is to find the minimum value of each of two comparison values:
- $${\it \Gamma}_{2}(10) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(010), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(110)\right] = {\rm Min}\left[0.2+ 0.01, 1.2 + 0.36\right]\hspace{0.15cm}\underline {= 0.21} \hspace{0.05cm},$$
- $${\it \Gamma}_{2}(11) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(011), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(111)\right] = {\rm Min}\left[0.2+ 0.09, 1.2 + 0.64\right]\hspace{0.15cm}\underline {= 0.29} \hspace{0.05cm}.$$
(3) The first and last solutions are correct:
- The sequence "$1011010$" can be recognized from the continuous path: "red – blue – red – red – blue – red – blue".
- On the other hand, no final statement can be made about the symbol $a_8$ at time $\nu = 8$:
- Only under the hypothesis $a_9 = 1$ and $a_{\rm 10} = 1$ one would decide for $a_8 = 0$, under other hypotheses for $a_8 = 1$.