Difference between revisions of "Aufgaben:Exercise 1.09Z: Extension and/or Puncturing"
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/General_Description_of_Linear_Block_Codes}} |
| − | + | [[File:EN_KC_Z_1_9.png|right|frame|Extension and puncturing]] | |
| − | + | Often you know a code that seems to be suitable for an application, but its code rate does not exactly match the specifications. | |
| − | + | There are several possibilities for rate adaptation: | |
| + | |||
| + | '''Extension''': | ||
| + | <br>Starting from the $(n, \, k)$ code whose parity-check matrix $\mathbf{H}$ is given, one obtains a $(n+1, \, k)$ code by extending the parity-check matrix by one row and one column and adding zeros and ones to the new matrix elements according to the upper graph. So, one adds a new parity bit | ||
| + | :$$x_{n+1} = x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n$$ | ||
| + | and thus a new parity-check equation is added, which is considered in $\mathbf{H}\hspace{0.05cm}'$ . | ||
| + | |||
| + | '''Puncturing''': | ||
| + | <br>According to the figure below, one arrives at a $(n-1, \, k)$ code of larger rate by omitting a parity bit and a parity-check equation, which is equivalent to deleting one row and one column from the parity-check matrix $\mathbf{H}$ . | ||
| + | |||
| + | '''Shortening''': | ||
| + | <br>If an information bit is omitted instead of a parity bit, the result is a $(n-1, \, k-1)$ code of smaller rate. | ||
| − | |||
| − | + | In this exercise, starting from a $(5, \, 2)$ block code | |
| − | + | ||
| − | + | :$$\mathcal{C} = \{ (0, 0, 0, 0, 0), \hspace{0.3cm} (0, 1, 0, 1, 1), \hspace{0.3cm} (1, 0, 1, 1, 0), \hspace{0.3cm} (1, 1, 1, 0, 1) \}$$ | |
| + | |||
| + | the following codes are to constructed and analyzed: | ||
| + | *one $(6, \, 2)$ code by single extension, | ||
| − | *$\ | + | *one $(7, \, 2)$ code by extending it again, |
| − | * | + | *one $(4, \, 2)$ code by puncturing. |
| − | |||
| − | + | The parity-check matrix and the generator matrix of the systematic $(5, \, 2)$ code are: | |
| − | + | :$${ \boldsymbol{\rm H}}_{(5,\ 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.3cm} \Leftrightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{(5,\ 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| − | + | Hints : | |
| − | + | *This exercise belongs to the chapter [[Channel_Coding/General_Description_of_Linear_Block_Codes|"General Description of Linear Block Codes"]]. | |
| − | + | *In the [[Aufgaben:Exercise_1.09:_Extended_Hamming_Code|"Exercise 1.9"]] it is exemplified how the $(7, \, 4, \, 3)$ Hamming code is turned into a $(8, \, 4, \, 4)$ code by extension. | |
| − | |||
| − | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | + | {Specify the characteristics of the given $(5, \, 2)$ code. | |
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $R \ = \ $ { 0.4 3% } |
| − | $ | + | $d_{\rm min} \ = \ $ { 3 3% } |
| − | { | + | {What code words does the $(6, \, 2)$ code have after expansion? |
|type="[]"} | |type="[]"} | ||
| − | - $(0 0 0 0 0 1), | + | - $(0 0 0 0 0 1), \ (0 1 0 1 1 0), \ (1 0 1 1 0 0), \ (1 1 1 0 1 1).$ |
| − | + $(0 0 0 0 0 0), | + | + $(0 0 0 0 0 0), \ (0 1 0 1 1 1), \ (1 0 1 1 0 1), \ (1 1 1 0 1 0).$ |
| − | { | + | {Specify the characteristics of the extended $(6, \, 2)$ code. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $R \ = \ $ { 0.333 3% } |
| − | $ | + | $d_{\rm min} \ = \ $ { 4 3% } |
| − | { | + | {What is the systematic generator matrix $\boldsymbol{\rm G}$ of the $(7, \, 2)$ code? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Row 1 of $\boldsymbol{\rm G} \text{:} \hspace{0.2cm} 1, \, 0, \, 1, \, 1, \, 0, \, 1, \, 0.$ |
| − | + | + | + Row 2 of $\boldsymbol{\rm G} \text{:} \hspace{0.2cm} 0, \, 1, \, 0, \, 1, \, 1, \, 1, \, 0.$ |
| − | { | + | {Specify the characteristics of the extended $(7, \, 2)$ code. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $R \ = \ $ { 0.266 3% } |
| − | $ | + | $d_{\rm min} \ = \ $ { 4 3% } |
| − | { | + | {Which statements are true for the $(4, \, 2)$ code (puncturing the last parity bit)? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The code rate is now $R = 2/4 = 0.5$. |
| − | + $C_{(4, 2)} = {(0, 0, 0, 0), (1, 0, 1, 1), | + | + $C_{(4,\ 2)} = \{(0, 0, 0, 0), \, (1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)\}$. |
| − | - | + | - The minimum distance remains unchanged from the $(5, \, 2)$ code. |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The rate of the $(5, \, 2)$ code is $R = 2/5 \ \underline{ = 0.4}$. |
| + | *From the given code, we further recognize the minimum distance $d_{\rm min} \ \underline{ = 3}$. | ||
| − | '''(2)''' | + | |
| + | |||
| + | '''(2)''' When extending from the $(5, \, 2)$ code to the $(6, \, 2)$ code, another parity bit is added. | ||
| + | *The code word thus has the form | ||
:$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6) = ( u_1, u_2, p_1, p_2, p_{3}, p_4) \hspace{0.05cm}.$$ | :$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6) = ( u_1, u_2, p_1, p_2, p_{3}, p_4) \hspace{0.05cm}.$$ | ||
| − | + | *For the added parity bit must be valid: | |
:$$p_4 = x_6 = x_1 \oplus x_2 \oplus x_3 \oplus x_4 \oplus x_5 \hspace{0.05cm}.$$ | :$$p_4 = x_6 = x_1 \oplus x_2 \oplus x_3 \oplus x_4 \oplus x_5 \hspace{0.05cm}.$$ | ||
| − | + | *That is, the new parity bit $p_{4}$ is chosen to result in an even number of ones in each code word ⇒ <u>Answer 2</u>. | |
| − | :$${ \boldsymbol{\rm H}}_{(6,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &0 &0 &0 &1 \end{pmatrix}$$ | + | |
| + | *Solving this task with the parity-check matrix, we get | ||
| + | :$${ \boldsymbol{\rm H}}_{(6,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &0 &0 &0 &1 \end{pmatrix}\hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &1 &0 &1\\ 0 &1 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | + | *The two rows of the generator matrix $\boldsymbol{\rm G}$ give two of the four code words, the modulo 2 sum gives the third, and finally the all zero word has to be considered. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' After extension from the $(5, \, 2)$ code to the $(6, \, 2)$ code. | ||
| + | *decreases the rate from $R = 2/5$ to $R = 2/6 \ \underline{= 0.333}$, | ||
| − | + | *increases the minimum distance from $d_{\rm min} = 3$ to $d_{\rm min} \ \underline{= 4}$ . | |
| − | |||
| − | |||
| − | : | + | <u>In general:</u> Extending a code, the rate decreases and the minimum distance increases by $1$ $($only if $d_{\rm min}$ was odd before$)$. |
| − | |||
| − | |||
| − | |||
| − | + | '''(4)''' Using the same procedure as in subtask '''(3)''', we obtain | |
| + | :$${ \boldsymbol{\rm H}}_{(7,\hspace{0.05cm} 2)} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm H}}_{{\rm (7,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 0 &0 &0 &0 &0 &0 &1 \end{pmatrix}\hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &1 &0 &1 &0 \\ 0 &1 &0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| + | ⇒ <u>Both answers</u> are correct. | ||
| − | '''(6)''' | + | |
| + | |||
| + | '''(5)''' The code rate is now $R = 2/7 \ \underline{=0.266}$. | ||
| + | *The minimum distance is still $d_{\rm min} \ \underline{= 4}$, as can be seen from the $(7, \, 2)$ code words: | ||
| + | :$$\mathcal{C} = \{ (0, 0, 0, 0, 0, 0, 0), \hspace{0.3cm}(0, 1, 0, 1, 1, 1, 0), \hspace{0.3cm}(1, 0, 1, 1, 0, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1, 0, 0) \}\hspace{0.05cm}.$$ | ||
| + | |||
| + | <u>In general:</u> If the minimum distance of a code is even, it cannot be increased by extension. | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Correct are the <u>statements 1 and 2</u>: | ||
| + | *By crossing out the last row and the last column, we obtain for parity-check matrix and generator matrix, respectively (each in systematic form): | ||
:$${ \boldsymbol{\rm H}}_{(4,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 \\ 1 &1 &0 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (4,\hspace{0.05cm} 2)}} = \begin{pmatrix} 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm H}}_{(4,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 \\ 1 &1 &0 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (4,\hspace{0.05cm} 2)}} = \begin{pmatrix} 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | + | *From the generator matrix we get the mentioned code words $(1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)$ as row sum as well as the null word $(0, 0, 0, 0)$. | |
| + | *The minimum distance of this code is $d_{\rm min}= 2$, which is smaller than the minimum distance $d_{\rm min}= 3$ of the $(5, \, 2)$ code. | ||
| − | <u> | + | |
| − | + | <u>In general:</u> Puncturing makes $d_{\rm min}$ smaller by $1$ (if it was even before) or it stays the same. | |
| − | + | ||
| + | *This can be illustrated by generating the $(3, \, 2)$ block code by another puncturing (of the parity bit $p_{2}$). | ||
| + | |||
| + | *This code $ \mathcal{C} = \{ (0, 0, 0), \hspace{0.3cm}(0, 1, 1), \hspace{0.3cm}(1, 0, 1), \hspace{0.3cm}(1, 1, 0) \}$ has the same minimum distance $d_{\rm min}= 2$ as the $(4, \, 2)$ code. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^1.4 Linear Block Code Description^]] |
| − | |||
| − | ^]] | ||
Latest revision as of 15:37, 11 July 2022
Often you know a code that seems to be suitable for an application, but its code rate does not exactly match the specifications.
There are several possibilities for rate adaptation:
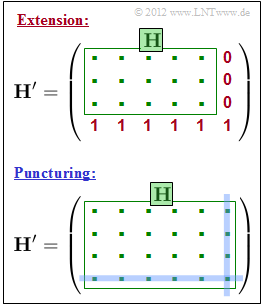
Extension:
Starting from the $(n, \, k)$ code whose parity-check matrix $\mathbf{H}$ is given, one obtains a $(n+1, \, k)$ code by extending the parity-check matrix by one row and one column and adding zeros and ones to the new matrix elements according to the upper graph. So, one adds a new parity bit
- $$x_{n+1} = x_1 \oplus x_2 \oplus ... \hspace{0.05cm} \oplus x_n$$
and thus a new parity-check equation is added, which is considered in $\mathbf{H}\hspace{0.05cm}'$ .
Puncturing:
According to the figure below, one arrives at a $(n-1, \, k)$ code of larger rate by omitting a parity bit and a parity-check equation, which is equivalent to deleting one row and one column from the parity-check matrix $\mathbf{H}$ .
Shortening:
If an information bit is omitted instead of a parity bit, the result is a $(n-1, \, k-1)$ code of smaller rate.
In this exercise, starting from a $(5, \, 2)$ block code
- $$\mathcal{C} = \{ (0, 0, 0, 0, 0), \hspace{0.3cm} (0, 1, 0, 1, 1), \hspace{0.3cm} (1, 0, 1, 1, 0), \hspace{0.3cm} (1, 1, 1, 0, 1) \}$$
the following codes are to constructed and analyzed:
- one $(6, \, 2)$ code by single extension,
- one $(7, \, 2)$ code by extending it again,
- one $(4, \, 2)$ code by puncturing.
The parity-check matrix and the generator matrix of the systematic $(5, \, 2)$ code are:
- $${ \boldsymbol{\rm H}}_{(5,\ 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.3cm} \Leftrightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{(5,\ 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
Hints :
- This exercise belongs to the chapter "General Description of Linear Block Codes".
- In the "Exercise 1.9" it is exemplified how the $(7, \, 4, \, 3)$ Hamming code is turned into a $(8, \, 4, \, 4)$ code by extension.
Questions
Solution
- From the given code, we further recognize the minimum distance $d_{\rm min} \ \underline{ = 3}$.
(2) When extending from the $(5, \, 2)$ code to the $(6, \, 2)$ code, another parity bit is added.
- The code word thus has the form
- $$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6) = ( u_1, u_2, p_1, p_2, p_{3}, p_4) \hspace{0.05cm}.$$
- For the added parity bit must be valid:
- $$p_4 = x_6 = x_1 \oplus x_2 \oplus x_3 \oplus x_4 \oplus x_5 \hspace{0.05cm}.$$
- That is, the new parity bit $p_{4}$ is chosen to result in an even number of ones in each code word ⇒ Answer 2.
- Solving this task with the parity-check matrix, we get
- $${ \boldsymbol{\rm H}}_{(6,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm H}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &0 &0 &0\\ 1 &1 &0 &1 &0 &0\\ 0 &1 &0 &0 &1 &0\\ 1 &1 &0 &0 &0 &1 \end{pmatrix}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} = \begin{pmatrix} 1 &0 &1 &1 &0 &1\\ 0 &1 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
- The two rows of the generator matrix $\boldsymbol{\rm G}$ give two of the four code words, the modulo 2 sum gives the third, and finally the all zero word has to be considered.
(3) After extension from the $(5, \, 2)$ code to the $(6, \, 2)$ code.
- decreases the rate from $R = 2/5$ to $R = 2/6 \ \underline{= 0.333}$,
- increases the minimum distance from $d_{\rm min} = 3$ to $d_{\rm min} \ \underline{= 4}$ .
In general: Extending a code, the rate decreases and the minimum distance increases by $1$ $($only if $d_{\rm min}$ was odd before$)$.
(4) Using the same procedure as in subtask (3), we obtain
- $${ \boldsymbol{\rm H}}_{(7,\hspace{0.05cm} 2)} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 1 &1 &1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm H}}_{{\rm (7,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &0 &0 &0 &0\\ 1 &1 &0 &1 &0 &0 &0\\ 0 &1 &0 &0 &1 &0 &0\\ 1 &1 &0 &0 &0 &1 &0\\ 0 &0 &0 &0 &0 &0 &1 \end{pmatrix}\hspace{0.15cm} \Rightarrow\hspace{0.15cm} { \boldsymbol{\rm G}}_{{\rm (6,\hspace{0.05cm} 2)\hspace{0.05cm}sys}} \hspace{-0.05cm}=\hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 &1 &0 &1 &0 \\ 0 &1 &0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm}.$$
⇒ Both answers are correct.
(5) The code rate is now $R = 2/7 \ \underline{=0.266}$.
- The minimum distance is still $d_{\rm min} \ \underline{= 4}$, as can be seen from the $(7, \, 2)$ code words:
- $$\mathcal{C} = \{ (0, 0, 0, 0, 0, 0, 0), \hspace{0.3cm}(0, 1, 0, 1, 1, 1, 0), \hspace{0.3cm}(1, 0, 1, 1, 0, 1, 0), \hspace{0.3cm}(1, 1, 1, 0, 1, 0, 0) \}\hspace{0.05cm}.$$
In general: If the minimum distance of a code is even, it cannot be increased by extension.
(6) Correct are the statements 1 and 2:
- By crossing out the last row and the last column, we obtain for parity-check matrix and generator matrix, respectively (each in systematic form):
- $${ \boldsymbol{\rm H}}_{(4,\hspace{0.05cm} 2)} = \begin{pmatrix} 1 &0 &1 &0 \\ 1 &1 &0 &1 \end{pmatrix} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} { \boldsymbol{\rm G}}_{{\rm (4,\hspace{0.05cm} 2)}} = \begin{pmatrix} 1 &0 &1 &1 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$
- From the generator matrix we get the mentioned code words $(1, 0, 1, 1), \, (0, 1, 0, 1), \, (1, 1, 1, 0)$ as row sum as well as the null word $(0, 0, 0, 0)$.
- The minimum distance of this code is $d_{\rm min}= 2$, which is smaller than the minimum distance $d_{\rm min}= 3$ of the $(5, \, 2)$ code.
In general: Puncturing makes $d_{\rm min}$ smaller by $1$ (if it was even before) or it stays the same.
- This can be illustrated by generating the $(3, \, 2)$ block code by another puncturing (of the parity bit $p_{2}$).
- This code $ \mathcal{C} = \{ (0, 0, 0), \hspace{0.3cm}(0, 1, 1), \hspace{0.3cm}(1, 0, 1), \hspace{0.3cm}(1, 1, 0) \}$ has the same minimum distance $d_{\rm min}= 2$ as the $(4, \, 2)$ code.