Difference between revisions of "Aufgaben:Exercise 4.1: About the Gram-Schmidt Process"
m (Guenter moved page Eercise 4.1: About the Gram-Schmidt Process to Exercise 4.1: About the Gram-Schmidt Process) |
|||
| (32 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} |
| − | [[File:P_ID1994__Dig_A_4_1.png|right|frame| | + | [[File:P_ID1994__Dig_A_4_1.png|right|frame|Specification for the Gram-Schmidt process]] |
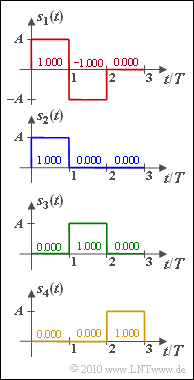
| − | + | For the four signals $s_1(t), \, \text{...} \, , s_4(t)$ defined by the figure, the three resulting basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$ are to be determined by applying the Gram-Schmidt process, so that for the signals with $i = 1, \, \text{...} \, , 4$ can be written: | |
:$$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$ | :$$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$ | ||
| − | In | + | *In subtask '''(1)''', let $A^2 = 1 \ \rm mW$ and $T = 1 \ \rm µ s$. |
| + | |||
| + | *In the later subtasks, the amplitude and the time are normalized quantities: $A = 1$, $T = 1$. | ||
| + | |||
| + | *Thus, both the coefficients $s_{\it ij}$ and the basis functions $\varphi_{\it j}(t)$ $($with $j = 1,\ 2,\ 3)$ are dimensionless quantities. | ||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| + | |||
| + | *Reference is made in particular to the sections [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#Orthonormal_basis_functions|"Orthonormal basis functions"]] and [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process|"Gram-Schmidt process"]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the units of the following quantities with $A^2 = 1 \, \rm mW$ and $T = 1 \, {\rm µ s}$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The basis functions $\varphi_j(t)$ are dimensionless. |
| − | + | + | + The basis functions $\varphi_j(t)$ have the unit $\rm \sqrt{\rm s}$. |
| + | - The coefficients $s_{\it ij}$ are dimensionless. | ||
| + | + The coefficients $s_{\it ij}$ have the unit $\rm \sqrt{\rm Ws}$. | ||
| + | |||
| + | {Perform the first step of the Gram-Schmidt process. As for the other tasks, let $A = 1$ and $T = 1$ hold. | ||
| + | |type="{}"} | ||
| + | $s_{\rm 11} \ = \ $ { 1.414 3% } | ||
| + | $s_{\rm 12} \ = \ $ { 0. } | ||
| + | $s_{\rm 13} \ = \ $ { 0. } | ||
| + | |||
| + | {What are the coefficients of the signal $s_2(t)$ with $A = 1$ and $T = 1$? | ||
| + | |type="{}"} | ||
| + | $s_{\rm 21} \ = \ $ { 0.707 3% } | ||
| + | $s_{\rm 22} \ = \ $ { 0.707 3% } | ||
| + | $s_{\rm 23} \ = \ $ { 0. } | ||
| + | |||
| + | {What are the coefficients of the signal $s_3(t)$ with $A = 1$ and $T = 1$? | ||
| + | |type="{}"} | ||
| + | $s_{\rm 31} \ = \ $ { -0.72821--0.68579 } | ||
| + | $s_{\rm 32} \ = \ $ { 0.707 3% } | ||
| + | $s_{\rm 33} \ = \ $ { 0. } | ||
| − | { | + | {What are the coefficients of the signal $s_4(t)$ with $A = 1$ and $T = 1$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $s_{\rm 41} \ = \ $ { 0. } |
| + | $s_{\rm 42} \ = \ $ { 0. } | ||
| + | $s_{\rm 43} \ = \ $ { 1 3% } | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Solutions 2 and 4</u> are correct: |
| − | '''(2)''' | + | *Every orthonormal basis function should have energy $1$, that is, it must hold: |
| − | '''(3)''' | + | :$$||\varphi_j(t)||^2 = \int_{-\infty}^{+\infty}\varphi_j(t)^2\,{\rm d} t = 1 |
| − | '''(4)''' | + | \hspace{0.05cm}.$$ |
| − | '''(5)''' | + | *For this condition to be satisfied, the basis function must have unit $\rm \sqrt{\rm s}$. |
| − | + | *Another equation to be considered is | |
| + | :$$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t).$$ | ||
| + | *Like the parameter $A$, the signals themselves have the unit $\rm \sqrt{\rm W}$. | ||
| + | *Because of the unit $\rm \sqrt{\rm 1/s}$ of $\varphi_{ j}(t)$, this equation can be satisfied with the correct dimension only if the coefficients $s_{\it ij}$ are given with the unit $\rm \sqrt{\rm Ws}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' The energy of the signal $s_1(t)$ is equal to $E_1 = 2$. | ||
| + | *It follows for the norm, the basis function $\varphi_1(t)$ and the coefficient $s_{\rm 11}$: | ||
| + | :$$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} | ||
| + | s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } | ||
| + | \hspace{0.05cm}.$$ | ||
| + | *The other coefficients are $\underline {s_{\rm 12} = s_{\rm 13} = 0}$, since the associated basis functions have not been found at all yet, while $\varphi_1(t)$ is equal in form to $s_1(t)$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Since at most two basis functions are found after considering $s_2(t)$ ⇒ $s_{\rm 23} \hspace{0.15cm} \underline{= 0}$ holds with certainty. On the other hand one obtains | ||
| + | *for the coefficient | ||
| + | :$$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} | ||
| + | s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } | ||
| + | \hspace{0.05cm};$$ | ||
| + | |||
| + | *for the auxiliary function $\theta_2(t)$: | ||
| + | :$$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = \left\{ \begin{array}{c} 1 - 0.707 \cdot 0.707 = 0.5\\ | ||
| + | 0 - 0.707 \cdot (-0.707) = 0.5 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} 0 \le t < 1 | ||
| + | \\ 1 \le t < 2 \\ \end{array} | ||
| + | \hspace{0.05cm}; $$ | ||
| + | |||
| + | *for the second basis function: | ||
| + | :$$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||},\hspace{0.2cm} | ||
| + | ||\theta_2(t)|| = \sqrt{0.5^2 + 0.5^2} = \sqrt{0.5} \approx 0.707$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \varphi_2(t) = \left\{ \begin{array}{c} 0.5/0.707 = 0.707\\ | ||
| + | 0 \end{array} \right.\quad | ||
| + | \begin{array}{*{1}c} 0 \le t < 2 | ||
| + | \\ 2 \le t < 3 \\ \end{array} | ||
| + | \hspace{0.05cm}; $$ | ||
| + | |||
| + | *and finally for the second coefficient | ||
| + | :$$s_{22} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 1 \cdot 0.707 + 0 \cdot 0.707 \hspace{0.1cm}\hspace{0.15cm}\underline { = 0.707} | ||
| + | \hspace{0.05cm}.$$ | ||
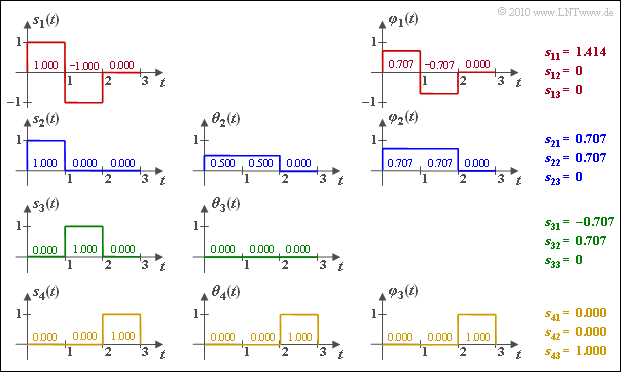
| + | [[File:P_ID1995__Dig_A_4_1c.png|right|frame|Gram-Schmidt calculations]] | ||
| + | |||
| + | The calculations are illustrated in the graph below. | ||
| + | |||
| + | |||
| + | '''(4)''' It can be seen immediately that $s_3(t)$ can be expressed as a linear combination of $s_1(t)$ and $s_2(t)$. | ||
| + | :$$s_{3}(t) = -s_{1}(t) + s_{2}(t),$$ | ||
| + | :$$s_{31} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{11} + s_{21} = -1.414 + 0.707 = \hspace{0.1cm}\hspace{0.15cm}\underline {-0.707}\hspace{0.05cm},$$ | ||
| + | :$$s_{32} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{12} + s_{22} = 0 + 0.707 \hspace{0.1cm}\underline {= 0.707}\hspace{0.05cm},$$ | ||
| + | :$$s_{33} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{13} + s_{23} = 0 + 0 \hspace{0.1cm}\underline {= 0}\hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| + | '''(5)''' The range $2 ≤ t ≤ 3$ is not covered by $\varphi_1(t)$ and $\varphi_2(t)$. | ||
| + | *Therefore, $s_4(t)$ provides the new basis function $\varphi_3(t)$. | ||
| + | *Since $s_4(t)$ has components only in the range $2 ≤ t ≤ 3$ and $||s_4(t)|| = 1$, we obtain $\varphi_3(t) = s_4(t)$ as well as | ||
| + | :$$s_{41} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{42} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1} \hspace{0.05cm}. $$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.1 Basis Functions & Vector Spaces^]] |
Latest revision as of 13:56, 13 July 2022
For the four signals $s_1(t), \, \text{...} \, , s_4(t)$ defined by the figure, the three resulting basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$ are to be determined by applying the Gram-Schmidt process, so that for the signals with $i = 1, \, \text{...} \, , 4$ can be written:
- $$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$
- In subtask (1), let $A^2 = 1 \ \rm mW$ and $T = 1 \ \rm µ s$.
- In the later subtasks, the amplitude and the time are normalized quantities: $A = 1$, $T = 1$.
- Thus, both the coefficients $s_{\it ij}$ and the basis functions $\varphi_{\it j}(t)$ $($with $j = 1,\ 2,\ 3)$ are dimensionless quantities.
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- Reference is made in particular to the sections "Orthonormal basis functions" and "Gram-Schmidt process".
Questions
Solution
- Every orthonormal basis function should have energy $1$, that is, it must hold:
- $$||\varphi_j(t)||^2 = \int_{-\infty}^{+\infty}\varphi_j(t)^2\,{\rm d} t = 1 \hspace{0.05cm}.$$
- For this condition to be satisfied, the basis function must have unit $\rm \sqrt{\rm s}$.
- Another equation to be considered is
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t).$$
- Like the parameter $A$, the signals themselves have the unit $\rm \sqrt{\rm W}$.
- Because of the unit $\rm \sqrt{\rm 1/s}$ of $\varphi_{ j}(t)$, this equation can be satisfied with the correct dimension only if the coefficients $s_{\it ij}$ are given with the unit $\rm \sqrt{\rm Ws}$.
(2) The energy of the signal $s_1(t)$ is equal to $E_1 = 2$.
- It follows for the norm, the basis function $\varphi_1(t)$ and the coefficient $s_{\rm 11}$:
- $$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm}.$$
- The other coefficients are $\underline {s_{\rm 12} = s_{\rm 13} = 0}$, since the associated basis functions have not been found at all yet, while $\varphi_1(t)$ is equal in form to $s_1(t)$.
(3) Since at most two basis functions are found after considering $s_2(t)$ ⇒ $s_{\rm 23} \hspace{0.15cm} \underline{= 0}$ holds with certainty. On the other hand one obtains
- for the coefficient
- $$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm};$$
- for the auxiliary function $\theta_2(t)$:
- $$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = \left\{ \begin{array}{c} 1 - 0.707 \cdot 0.707 = 0.5\\ 0 - 0.707 \cdot (-0.707) = 0.5 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 1 \\ 1 \le t < 2 \\ \end{array} \hspace{0.05cm}; $$
- for the second basis function:
- $$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||},\hspace{0.2cm} ||\theta_2(t)|| = \sqrt{0.5^2 + 0.5^2} = \sqrt{0.5} \approx 0.707$$
- $$\Rightarrow \hspace{0.3cm} \varphi_2(t) = \left\{ \begin{array}{c} 0.5/0.707 = 0.707\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 2 \\ 2 \le t < 3 \\ \end{array} \hspace{0.05cm}; $$
- and finally for the second coefficient
- $$s_{22} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 1 \cdot 0.707 + 0 \cdot 0.707 \hspace{0.1cm}\hspace{0.15cm}\underline { = 0.707} \hspace{0.05cm}.$$
The calculations are illustrated in the graph below.
(4) It can be seen immediately that $s_3(t)$ can be expressed as a linear combination of $s_1(t)$ and $s_2(t)$.
- $$s_{3}(t) = -s_{1}(t) + s_{2}(t),$$
- $$s_{31} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{11} + s_{21} = -1.414 + 0.707 = \hspace{0.1cm}\hspace{0.15cm}\underline {-0.707}\hspace{0.05cm},$$
- $$s_{32} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{12} + s_{22} = 0 + 0.707 \hspace{0.1cm}\underline {= 0.707}\hspace{0.05cm},$$
- $$s_{33} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{13} + s_{23} = 0 + 0 \hspace{0.1cm}\underline {= 0}\hspace{0.05cm}. $$
(5) The range $2 ≤ t ≤ 3$ is not covered by $\varphi_1(t)$ and $\varphi_2(t)$.
- Therefore, $s_4(t)$ provides the new basis function $\varphi_3(t)$.
- Since $s_4(t)$ has components only in the range $2 ≤ t ≤ 3$ and $||s_4(t)|| = 1$, we obtain $\varphi_3(t) = s_4(t)$ as well as
- $$s_{41} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{42} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1} \hspace{0.05cm}. $$