Difference between revisions of "Aufgaben:Exercise 4.2: AM/PM Oscillations"
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} |
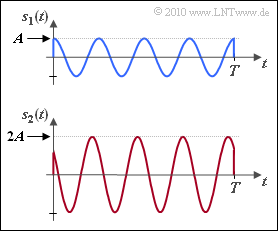
| − | [[File:P_ID1997__Dig_A_4_2.png|right|frame|AM/PM | + | [[File:P_ID1997__Dig_A_4_2.png|right|frame|Two possible AM/PM oscillations]] |
| − | + | We consider the signal set $\{s_i(t)\}$ with the indexing variable $i = 1, \ \text{...} \, M$. All signals $s_i(t)$ can be represented in the same way: | |
:$$s_i(t) = | :$$s_i(t) = | ||
\left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| − | \\ {\rm | + | \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
| − | + | The signal duration $T$ is an integer multiple of $1/f_{\rm T}$, where $f_{\rm T}$ is the signal frequency ("carrier frequency"). | |
| − | * | + | *For the sketch, the duration of the energy-limited signals is $T = 4/f_{\rm T}$, i.e. exactly four oscillations are recognized within $T$ in each case. |
| − | |||
| + | *The individual signals $s_i(t)$ differ in amplitude $(A_i)$ and/or phase $(\phi_i)$. | ||
| − | + | ||
| + | For the two signals (shown in the graph) holds: | ||
:$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$ | :$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$ | ||
:$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$ | :$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$ | ||
| − | + | If we first restrict ourselves to these two signals $s_1(t)$ and $s_2(t)$, they can be completely described by the basis functions $\varphi_1(t)$ and $\varphi_2(t)$. These are orthonormal to each other, that is, taking into account the time constraint on $T$ holds: | |
| − | :$$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm}, | + | :$$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm},$$ |
| − | \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 | + | :$$ \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | With these basis functions, the two signals can be represented as follows: | |
:$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$ | :$$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$ | ||
:$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | :$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | ||
| − | In | + | In subtask '''(7)''' we want to check whether all signals $s_i(t)$ according to the above definition $($with arbitrary amplitude $A_i$ and arbitrary phase $\phi_i)$ can be described by the following equation: |
:$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | :$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | ||
| − | + | The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are to be found here by the [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process|"Gram–Schmidt process"]], which was described in detail in the theory section. The required equations are summarized here again: | |
| − | :$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm | + | :$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm with}\hspace{0.4cm} |
s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} | s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} | ||
\hspace{0.05cm},\hspace{0.4cm} | \hspace{0.05cm},\hspace{0.4cm} | ||
| Line 45: | Line 46: | ||
| − | + | Notes: | |
| − | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | |
| − | * | + | |
| + | * For abbreviation, use the energy $E = 1/2 \cdot A^2 \cdot T$. | ||
| − | * | + | * Furthermore, the following trigonometric relation is given: |
| − | |||
:$$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$ | :$$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$ | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the energy and the "2–norm" of the signal $s_1(t)$, expressed by $E$? |
|type="{}"} | |type="{}"} | ||
$E_1\ = \ $ { 1 3% } $\ \cdot E$ | $E_1\ = \ $ { 1 3% } $\ \cdot E$ | ||
$||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | $||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \sqrt{E}$ | ||
| − | { | + | {What is the Gram–Schmidt basis function $\varphi_1(t)$? |
|type="[]"} | |type="[]"} | ||
- $\varphi_1(t) = \sqrt{E} \cdot {\rm cos}(2\pi f_{\rm T}t)$, | - $\varphi_1(t) = \sqrt{E} \cdot {\rm cos}(2\pi f_{\rm T}t)$, | ||
| Line 67: | Line 68: | ||
+ $\varphi_1(t) = \sqrt{2/T} \cdot {\rm cos}(2\pi f_{\rm T}t)$. | + $\varphi_1(t) = \sqrt{2/T} \cdot {\rm cos}(2\pi f_{\rm T}t)$. | ||
| − | { | + | {What is the relationship between $s_1(t)$ and $\varphi_1(t)$? |
|type="[]"} | |type="[]"} | ||
+ $s_1(t) = \sqrt{E} \cdot \varphi_1(t)$, | + $s_1(t) = \sqrt{E} \cdot \varphi_1(t)$, | ||
| Line 73: | Line 74: | ||
- $s_1(t) = \sqrt{2/T} \cdot \varphi_1(t)$. | - $s_1(t) = \sqrt{2/T} \cdot \varphi_1(t)$. | ||
| − | { | + | {What is the "inner product" $s_{\rm 21} = 〈 s_2(t) \cdot \varphi_1(t)〉$? |
|type="{}"} | |type="{}"} | ||
$s_{\rm 21} \ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 21} \ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
| − | { | + | {What is the auxiliary function $\theta_2(t)$? |
|type="[]"} | |type="[]"} | ||
- $\theta_2(t) = +\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, | - $\theta_2(t) = +\sqrt{2} \cdot A \cdot {\rm sin}(2\pi f_{\rm T}t)$, | ||
| Line 83: | Line 84: | ||
- $\theta_2(t) = \sqrt{2/T} \cdot {\rm sin}(2\pi f_{\rm T}t)$. | - $\theta_2(t) = \sqrt{2/T} \cdot {\rm sin}(2\pi f_{\rm T}t)$. | ||
| − | { | + | {Give the coefficients of $s_2(t) = s_{\rm 21} \cdot \varphi_1(t) + s_{\rm 22} \cdot \varphi_2(t)$. |
|type="{}"} | |type="{}"} | ||
$s_{\rm 21}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 21}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
$s_{\rm 22}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | $s_{\rm 22}\ = \ $ { 1.414 3% } $\ \cdot \sqrt{E}$ | ||
| − | { | + | {Which of the statements are generally true for the basis functions of the signal set $\{s_i(t)\}$ with $i = 1, \ \text{ ...} \ , M$, if $M \gg 2$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The number of basis functions is always $N = M$. |
| − | + | + | + The number of basis functions is always $N = 2$. |
| − | + | + | + Possible basis functions are cosine and (minus) sine. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The energy can be calculated using the following equation: |
:$$E_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | :$$E_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} | ||
\int_{0}^{T}A^2 \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2}\hspace{0.05cm}+\hspace{0.05cm} | \int_{0}^{T}A^2 \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2}\hspace{0.05cm}+\hspace{0.05cm} | ||
| Line 103: | Line 104: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *Here it is considered that $T$ is an even multiple of $1/f_{\rm T}$, so the second integral vanishes. |
| + | |||
| + | *Further: | ||
:$$||s_1(t)|| = \sqrt{E_1} = \sqrt{E} = \hspace{0.1cm}\hspace{0.15cm}\underline{1 \cdot\sqrt{E}} | :$$||s_1(t)|| = \sqrt{E_1} = \sqrt{E} = \hspace{0.1cm}\hspace{0.15cm}\underline{1 \cdot\sqrt{E}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' <u>Solution 3</u> is correct: The basis function $\varphi_1(t)$ is equal in form to $s_1(t)$, where holds: |
:$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{E}}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{1/2 \cdot A^2 \cdot T}} = \sqrt{{2}/{T}} | :$$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{E}}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{1/2 \cdot A^2 \cdot T}} = \sqrt{{2}/{T}} | ||
\cdot \cos(2\pi f_{\rm T}t ) | \cdot \cos(2\pi f_{\rm T}t ) | ||
| Line 114: | Line 117: | ||
| − | '''(3)''' | + | '''(3)''' <u>Solution 1</u> is correct since according to the equation given in '''(2)''': |
:$$s_1(t) = ||s_1(t)|| \cdot \varphi_1(t) = \sqrt{E} \cdot \varphi_1(t) | :$$s_1(t) = ||s_1(t)|| \cdot \varphi_1(t) = \sqrt{E} \cdot \varphi_1(t) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' Using the signal $s_2(t)$ according to the given information, the basis function $\varphi_1(t)$ according to subtask '''(2)''' and the given trigonometric relation we get: |
:$$s_{21} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = | :$$s_{21} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = | ||
\int_{0}^{T}2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) \cdot \sqrt{{2}/{T}} | \int_{0}^{T}2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) \cdot \sqrt{{2}/{T}} | ||
| Line 129: | Line 132: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *The second component yields the value $0$ (orthogonality). The first component yields: |
:$$s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \frac{1}{\sqrt{2}}\cdot \frac{T}{2} = \sqrt{A^2 \cdot T} = \sqrt{2E} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot \sqrt{E}} | :$$s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \frac{1}{\sqrt{2}}\cdot \frac{T}{2} = \sqrt{A^2 \cdot T} = \sqrt{2E} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot \sqrt{E}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' According to the Gram–Schmidt process, we obtain |
:$$\theta_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm} = | :$$\theta_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm} = | ||
2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) - \sqrt{A^2 \cdot T} | 2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) - \sqrt{A^2 \cdot T} | ||
| Line 144: | Line 147: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | *With $\cos {(\pi/4)} = \sin (\pi/4) =\sqrt{0.5}$ it follows: |
:$$\theta_2(t) = - \sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t ) | :$$\theta_2(t) = - \sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Therefore, <u>solution 2</u> is correct. |
| − | '''(6)''' | + | '''(6)''' Analogous to subtask '''(2)''', the orthonormal basis function $\varphi_2(t)$ is given by |
:$$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||} = - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t ) | :$$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||} = - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, the signal $s_2(t)$ can be represented by $s_{21}$ according to subtask '''(4)''' as follows: |
:$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}, \hspace{0.2cm}s_{21} = \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm},$$ | :$$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}, \hspace{0.2cm}s_{21} = \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm},$$ | ||
:$$s_{22}\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\theta_2(t)}{\varphi_2(t)} = \frac{-\sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t )} | :$$s_{22}\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\theta_2(t)}{\varphi_2(t)} = \frac{-\sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t )} | ||
| Line 162: | Line 165: | ||
| − | '''(7)''' | + | '''(7)''' We consider very many energy-limited signals $(M \gg 2)$ of the following form: |
:$$s_i(t)= | :$$s_i(t)= | ||
\left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
\begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, | ||
| − | \\ {\rm | + | \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$ |
| − | + | The indexing variable can take the values $i = 1, 2, \ \text{...} \ , M$. Then holds: | |
| − | * | + | * All $M$ signals can be completely described by only $N = 2$ basis functions: |
:$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | :$$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$ | ||
| − | * | + | |
| + | * If one proceeds according to the Gram–Schmidt process, one obtains for the two basis functions | ||
:$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1)\hspace{0.05cm},\hspace{0.5cm} | :$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1)\hspace{0.05cm},\hspace{0.5cm} | ||
\varphi_2(t) = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1 \pm {\pi}/{2})\hspace{0.05cm}.$$ | \varphi_2(t) = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1 \pm {\pi}/{2})\hspace{0.05cm}.$$ | ||
| − | * | + | |
| − | * | + | * The sign in the argument of the second cosine function $(± \pi/2)$ is not unique. Rather, the sign of $s_{i 2}$ also depends on whether the plus sign or the minus sign was used for $\varphi_2(t)$. |
| + | |||
| + | * However, possible basis functions that then lead to other coefficients are also: | ||
:$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},\hspace{0.5cm} | :$$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},\hspace{0.5cm} | ||
\varphi_2(t) \pm \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}.$$ | \varphi_2(t) \pm \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}.$$ | ||
| − | + | ⇒ So the <u>solutions 2 and 3</u> are correct. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.1 Basis Functions & Vector Spaces^]] |
Latest revision as of 17:11, 13 July 2022
We consider the signal set $\{s_i(t)\}$ with the indexing variable $i = 1, \ \text{...} \, M$. All signals $s_i(t)$ can be represented in the same way:
- $$s_i(t) = \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
The signal duration $T$ is an integer multiple of $1/f_{\rm T}$, where $f_{\rm T}$ is the signal frequency ("carrier frequency").
- For the sketch, the duration of the energy-limited signals is $T = 4/f_{\rm T}$, i.e. exactly four oscillations are recognized within $T$ in each case.
- The individual signals $s_i(t)$ differ in amplitude $(A_i)$ and/or phase $(\phi_i)$.
For the two signals (shown in the graph) holds:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2A \cdot \cos(2\pi f_{\rm T}t + \pi/4) \hspace{0.05cm}. $$
If we first restrict ourselves to these two signals $s_1(t)$ and $s_2(t)$, they can be completely described by the basis functions $\varphi_1(t)$ and $\varphi_2(t)$. These are orthonormal to each other, that is, taking into account the time constraint on $T$ holds:
- $$\int_{0}^{T}\varphi_1^2(t) \, {\rm d} t = \int_{0}^{T}\varphi_2^2(t) \, {\rm d} t = 1 \hspace{0.05cm},$$
- $$ \int_{0}^{T}\varphi_1(t) \cdot \varphi_2(t)\, {\rm d} t = 0 \hspace{0.05cm}.$$
With these basis functions, the two signals can be represented as follows:
- $$s_1(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{11} \cdot \varphi_1(t) \hspace{0.05cm},$$
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}. $$
In subtask (7) we want to check whether all signals $s_i(t)$ according to the above definition $($with arbitrary amplitude $A_i$ and arbitrary phase $\phi_i)$ can be described by the following equation:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$
The basis functions $\varphi_1(t)$ and $\varphi_2(t)$ are to be found here by the "Gram–Schmidt process", which was described in detail in the theory section. The required equations are summarized here again:
- $$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}\hspace{0.4cm}{\rm with}\hspace{0.4cm} s_{11} = ||s_1(t)|| = \sqrt{\int_{0}^{T}s_1^2(t) \, {\rm d} t} \hspace{0.05cm},\hspace{0.4cm} s_{21} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}s_2(t) \cdot \varphi_1(t)\, {\rm d} t \hspace{0.05cm},$$
- $$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm}, \hspace{0.2cm} \varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||}\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- For abbreviation, use the energy $E = 1/2 \cdot A^2 \cdot T$.
- Furthermore, the following trigonometric relation is given:
- $$\cos(\alpha \pm \beta) = \cos(\alpha )\cdot \cos(\beta) \mp \sin(\alpha )\cdot \sin(\beta)\hspace{0.05cm}.$$
Questions
Solution
- $$E_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0}^{T}A^2 \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2}\hspace{0.05cm}+\hspace{0.05cm} \frac{A^2 }{2}\int_{0}^{T} \cos(4\pi f_{\rm T}t )\, {\rm d} t = \frac{A^2 \cdot T}{2} \hspace{0.05cm}\underline{= 1 \cdot E} \hspace{0.05cm}. $$
- Here it is considered that $T$ is an even multiple of $1/f_{\rm T}$, so the second integral vanishes.
- Further:
- $$||s_1(t)|| = \sqrt{E_1} = \sqrt{E} = \hspace{0.1cm}\hspace{0.15cm}\underline{1 \cdot\sqrt{E}} \hspace{0.05cm}.$$
(2) Solution 3 is correct: The basis function $\varphi_1(t)$ is equal in form to $s_1(t)$, where holds:
- $$\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{E}}= \frac{A \cdot \cos(2\pi f_{\rm T}t )}{\sqrt{1/2 \cdot A^2 \cdot T}} = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
(3) Solution 1 is correct since according to the equation given in (2):
- $$s_1(t) = ||s_1(t)|| \cdot \varphi_1(t) = \sqrt{E} \cdot \varphi_1(t) \hspace{0.05cm}.$$
(4) Using the signal $s_2(t)$ according to the given information, the basis function $\varphi_1(t)$ according to subtask (2) and the given trigonometric relation we get:
- $$s_{21} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_1(t) \hspace{-0.1cm} > \hspace{0.1cm} = \int_{0}^{T}2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t = $$
- $$\Rightarrow \hspace{0.3cm}s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\cos({\pi}/{4}) \cdot \cos^2(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.1cm}- \sqrt{\frac{8A^2}{T}}\cdot \int_{0}^{T}\sin({\pi}/{4}) \cdot \sin(2\pi f_{\rm T}t )\cdot \cos(2\pi f_{\rm T}t )\, {\rm d} t \hspace{0.05cm}. $$
- The second component yields the value $0$ (orthogonality). The first component yields:
- $$s_{21} = \sqrt{\frac{8A^2}{T}}\cdot \frac{1}{\sqrt{2}}\cdot \frac{T}{2} = \sqrt{A^2 \cdot T} = \sqrt{2E} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot \sqrt{E}} \hspace{0.05cm}.$$
(5) According to the Gram–Schmidt process, we obtain
- $$\theta_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_2(t) - s_{21} \cdot \varphi_1(t)\hspace{0.05cm} = 2A \cdot \cos(2\pi f_{\rm T}t + {\pi}/{4}) - \sqrt{A^2 \cdot T} \cdot \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t ) $$
- $$\Rightarrow \hspace{0.3cm}\theta_2(t) = 2A \cdot \cos({\pi}/{4})\cdot \cos(2\pi f_{\rm T}t )\hspace{0.1cm} - \hspace{0.1cm} 2A \cdot \sin({\pi}/{4})\cdot \sin(2\pi f_{\rm T}t )\hspace{0.1cm} - \sqrt{2} \cdot A \cdot \cos(2\pi f_{\rm T}t ) \hspace{0.05cm}. $$
- With $\cos {(\pi/4)} = \sin (\pi/4) =\sqrt{0.5}$ it follows:
- $$\theta_2(t) = - \sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
- Therefore, solution 2 is correct.
(6) Analogous to subtask (2), the orthonormal basis function $\varphi_2(t)$ is given by
- $$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||} = - \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t ) \hspace{0.05cm}.$$
- Thus, the signal $s_2(t)$ can be represented by $s_{21}$ according to subtask (4) as follows:
- $$s_2(t)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} s_{21} \cdot \varphi_1(t) + s_{22} \cdot \varphi_2(t) \hspace{0.05cm}, \hspace{0.2cm}s_{21} = \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm},$$
- $$s_{22}\hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{\theta_2(t)}{\varphi_2(t)} = \frac{-\sqrt{2} \cdot A \cdot \sin(2\pi f_{\rm T}t )} {-\sqrt{2/T}\cdot \sin(2\pi f_{\rm T}t )} = \sqrt{2} \cdot \sqrt{1/2 \cdot A^2 \cdot T}\hspace{0.05cm} \underline{ = 1.414 \cdot \sqrt {E}}\hspace{0.05cm}.$$
(7) We consider very many energy-limited signals $(M \gg 2)$ of the following form:
- $$s_i(t)= \left\{ \begin{array}{c} A_i \cdot \cos(2\pi f_{\rm T}t + \phi_i) \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < T \hspace{0.05cm}, \\ {\rm otherwise}\hspace{0.05cm}. \\ \end{array}$$
The indexing variable can take the values $i = 1, 2, \ \text{...} \ , M$. Then holds:
- All $M$ signals can be completely described by only $N = 2$ basis functions:
- $$s_i(t)= s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) \hspace{0.05cm}. $$
- If one proceeds according to the Gram–Schmidt process, one obtains for the two basis functions
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1)\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) = \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t + \phi_1 \pm {\pi}/{2})\hspace{0.05cm}.$$
- The sign in the argument of the second cosine function $(± \pi/2)$ is not unique. Rather, the sign of $s_{i 2}$ also depends on whether the plus sign or the minus sign was used for $\varphi_2(t)$.
- However, possible basis functions that then lead to other coefficients are also:
- $$\varphi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{{2}/{T}} \cdot \cos(2\pi f_{\rm T}t )\hspace{0.05cm},\hspace{0.5cm} \varphi_2(t) \pm \sqrt{{2}/{T}} \cdot \sin(2\pi f_{\rm T}t )\hspace{0.05cm}.$$
⇒ So the solutions 2 and 3 are correct.