Difference between revisions of "Aufgaben:Exercise 1.11Z: Syndrome Decoding again"
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Linear_Block_Codes}} | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Linear_Block_Codes}} | ||
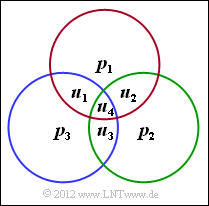
| − | [[File:P_ID2399__KC_Z_1_10.png|right|frame| | + | [[File:P_ID2399__KC_Z_1_10.png|right|frame|Parity-check chart]] |
| − | The same constellation is considered as in [[Aufgaben:Exercise_1.11:_Syndrome_Decoding|Exercise 1.11]] | + | The same constellation is considered as in [[Aufgaben:Exercise_1.11:_Syndrome_Decoding|"Exercise 1.11"]]: The decoding of a $(7, 4, 3)$ Hamming code with the parity-check matrix |
:$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | Accordingly, the generator | + | Accordingly, the generator matrix is: |
:$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$ | ||
| − | + | In [[Channel_Coding/Decoding_of_Linear_Block_Codes#Principle_of_syndrome_decoding|"syndrome decoding"]] one forms from the received vector $\underline{y}$ the syndrome $\underline{s}$ according to the equation | |
:$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$ | :$$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$ | ||
| − | + | With this result, any single error in the code word can be corrected in the Hamming code under consideration. | |
| − | * | + | *In the error-free case $\underline{s} = \underline{s}_{0} = (0, 0, 0)$. |
| − | * | + | |
| + | *But even three transmission errors may result in $\underline{s}_{0} = (0, 0, 0)$, so these errors remain undetected. | ||
| Line 25: | Line 26: | ||
| − | + | Hints: | |
| − | * | + | * The exercise belongs to the chapter [[Channel_Coding/Decoding_of_Linear_Block_Codes|"Decoding of Linear Block Codes"]]. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * For more information on syndrome decoding, see the specification sheet for [[Aufgaben:Exercise_1.11:_Syndrome_Decoding|"Exercise 1.11"]]. | ||
| + | |||
| + | * The graph illustrates the three parity-check equations corresponding to the parity-check matrix: | ||
| + | **first row: red circle, | ||
| + | **second row: green circle, | ||
| + | **third row: blue circle. | ||
| − | === | + | |
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Is it a systematic code? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
| − | { | + | {With received vector $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$. Is this a valid code word? |
|type="()"} | |type="()"} | ||
| − | + | + | + Yes, |
| − | - | + | - No. |
| − | { | + | {What syndrome results with this received word? |
|type="()"} | |type="()"} | ||
+ $\underline{s} = \underline{s}_{0} = (0, 0, 0),$ | + $\underline{s} = \underline{s}_{0} = (0, 0, 0),$ | ||
| Line 54: | Line 57: | ||
- $\underline{s} = \underline{s}_{7} = (1, 1, 1).$ | - $\underline{s} = \underline{s}_{7} = (1, 1, 1).$ | ||
| − | { | + | {Which received words lead to the same syndrome as in subtask '''(3)'''? |
|type="[]"} | |type="[]"} | ||
- $\underline{y} = (1, 1, 0, 1, 0, 1, 0),$ | - $\underline{y} = (1, 1, 0, 1, 0, 1, 0),$ | ||
| Line 61: | Line 64: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The answer is <u>YES</u>, as can be seen from the given parity-check matrix $\mathbf{H}$: |
| − | * | + | *This contains a $3×3$ diagonal matrix at the end. |
| − | * | + | *The code words are therefore: |
:$$ \underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_{3}) \hspace{0.05cm}.$$ | :$$ \underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_{3}) \hspace{0.05cm}.$$ | ||
| Line 71: | Line 74: | ||
| − | '''(2)''' | + | '''(2)''' With this received vector $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$, all parity-check equations are satisfied: |
:$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$ | :$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$ | ||
| Line 77: | Line 80: | ||
:$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm}.$$ | :$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm}.$$ | ||
| − | + | Accordingly, the correct answer is <u>YES</u>. | |
| − | '''(3)''' | + | '''(3)''' It holds $\underline{s} = \underline{y} · \boldsymbol{\rm H}^{\rm T}$: |
| − | :$$ \underline{s} = \begin{pmatrix} 1 &0 &0 &1 &0 &1 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1\\ 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \end{pmatrix} = \underline{s}_0 \hspace{0.2cm} \Rightarrow\hspace{0.2cm} \hspace{0.15cm} \underline{ \rm | + | :$$ \underline{s} = \begin{pmatrix} 1 &0 &0 &1 &0 &1 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1\\ 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \end{pmatrix} = \underline{s}_0 \hspace{0.2cm} \Rightarrow\hspace{0.2cm} \hspace{0.15cm} \underline{ \rm Answer \hspace{0.15cm}1} \hspace{0.05cm}.$$ |
| − | '''(4)''' | + | '''(4)''' One could now for each $\underline{y}$ check the equation $\underline{y} · \boldsymbol{\rm H}^{\rm T} = (0, 0, 0)$. Now here the result shall be obtained in a different way: |
| − | *$\underline{y}= (1, 1, 0, 1, 0, 1, 0)$ | + | *$\underline{y}= (1, 1, 0, 1, 0, 1, 0)$ differs from $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$ in bit $u_{2}$, which is used only in the first two parity-check equations, but not in the last ⇒ $\underline{s} = \underline{s}_{6} = (1, 1, 0)$. |
| − | * | + | *Applying the parity-check equations to $\underline{y} = (0, 1, 0, 1, 0, 0, 1)$, we obtain $\underline{s} = \underline{s}_{0} = (0, 0, 0)$, as evidenced by the following calculation: |
:$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$ | :$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$ | ||
| Line 97: | Line 100: | ||
:$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm}.$$ | :$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm}.$$ | ||
| − | * | + | *The same result is obtained with the received vector $\underline{y} = (0, 1, 1, 0, 1, 0, 1),$ which differs from the vector $(1, 0, 0, 1, 0, 1, 0)$ in all seven bit positions: |
:$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm},$$ | :$$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm},$$ | ||
| Line 103: | Line 106: | ||
:$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm}.$$ | :$$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm}.$$ | ||
| − | + | So the correct answers are <u>answers 2 and 3</u>. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 12:24, 20 July 2022
The same constellation is considered as in "Exercise 1.11": The decoding of a $(7, 4, 3)$ Hamming code with the parity-check matrix
- $${ \boldsymbol{\rm H}}_{\rm } = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Accordingly, the generator matrix is:
- $${ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &0\\ 0 &0 &1 &0 &0 &1 &1\\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
In "syndrome decoding" one forms from the received vector $\underline{y}$ the syndrome $\underline{s}$ according to the equation
- $$\underline{s} = \underline{y} \cdot { \boldsymbol{\rm H}}^{\rm T} \in {\rm GF}(2^m) \hspace{0.05cm}.$$
With this result, any single error in the code word can be corrected in the Hamming code under consideration.
- In the error-free case $\underline{s} = \underline{s}_{0} = (0, 0, 0)$.
- But even three transmission errors may result in $\underline{s}_{0} = (0, 0, 0)$, so these errors remain undetected.
Hints:
- The exercise belongs to the chapter "Decoding of Linear Block Codes".
- For more information on syndrome decoding, see the specification sheet for "Exercise 1.11".
- The graph illustrates the three parity-check equations corresponding to the parity-check matrix:
- first row: red circle,
- second row: green circle,
- third row: blue circle.
Questions
Solution
- This contains a $3×3$ diagonal matrix at the end.
- The code words are therefore:
- $$ \underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_{3}) \hspace{0.05cm}.$$
(2) With this received vector $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$, all parity-check equations are satisfied:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm}.$$
Accordingly, the correct answer is YES.
(3) It holds $\underline{s} = \underline{y} · \boldsymbol{\rm H}^{\rm T}$:
- $$ \underline{s} = \begin{pmatrix} 1 &0 &0 &1 &0 &1 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 &0 &1\\ 1 &1 &0\\ 0 &1 &1\\ 1 &1 &1\\ 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \end{pmatrix} = \underline{s}_0 \hspace{0.2cm} \Rightarrow\hspace{0.2cm} \hspace{0.15cm} \underline{ \rm Answer \hspace{0.15cm}1} \hspace{0.05cm}.$$
(4) One could now for each $\underline{y}$ check the equation $\underline{y} · \boldsymbol{\rm H}^{\rm T} = (0, 0, 0)$. Now here the result shall be obtained in a different way:
- $\underline{y}= (1, 1, 0, 1, 0, 1, 0)$ differs from $\underline{y} = (1, 0, 0, 1, 0, 1, 0)$ in bit $u_{2}$, which is used only in the first two parity-check equations, but not in the last ⇒ $\underline{s} = \underline{s}_{6} = (1, 1, 0)$.
- Applying the parity-check equations to $\underline{y} = (0, 1, 0, 1, 0, 0, 1)$, we obtain $\underline{s} = \underline{s}_{0} = (0, 0, 0)$, as evidenced by the following calculation:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 0 \oplus 1 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 0 \oplus 1 \oplus 1 = 0 \hspace{0.05cm}.$$
- The same result is obtained with the received vector $\underline{y} = (0, 1, 1, 0, 1, 0, 1),$ which differs from the vector $(1, 0, 0, 1, 0, 1, 0)$ in all seven bit positions:
- $$u_1 \oplus u_2 \oplus u_4 \oplus p_1 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm},$$
- $$u_2 \oplus u_3 \oplus u_4 \oplus p_2 = 1 \oplus 1 \oplus 0 \oplus 0 = 0 \hspace{0.05cm},$$
- $$u_1 \oplus u_3 \oplus u_4 \oplus p_3 = 0 \oplus 1 \oplus 0 \oplus 1 = 0 \hspace{0.05cm}.$$
So the correct answers are answers 2 and 3.