Difference between revisions of "Aufgaben:Exercise 4.1Z: Other Basis Functions"
| (34 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} |
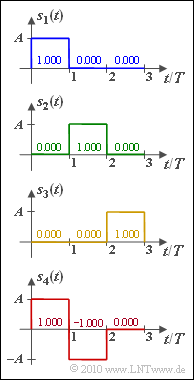
| − | [[File:P_ID1996__Dig_Z_4_1.png|right|frame| | + | [[File:P_ID1996__Dig_Z_4_1.png|right|frame|Energy-limited signals]] |
| − | + | This exercise pursues exactly the same goal as [[Aufgaben:Eercise_4.1:_About_the_Gram-Schmidt_Process|"Exercise 4.1"]]: | |
| − | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = | + | |
| − | + | For $M = 4$ energy-limited signals $s_i(t)$ with $i = 1, \ \text{...} \ , 4$, the $N$ required orthonormal basis functions $\varphi_{\it j}(t)$ are to be found, which must satisfy the following condition: | |
| + | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = | ||
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
0 \end{array} \right.\quad | 0 \end{array} \right.\quad | ||
| Line 12: | Line 13: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | With $M$ transmitted signals $s_i(t)$, already fewer basis functions $\varphi_{\it j}(t)$ can suffice, namely $N$. Thus, in general, $N ≤ M$. | ||
| + | |||
| + | These are exactly the same energy-limited signals $s_i(t)$ as in [[Aufgaben:Exercise_4.1:_About_the_Gram-Schmidt_Process|"Exercise 4.1"]]: | ||
| + | *The difference is the different order of the signals $s_i(t)$. | ||
| + | |||
| + | *In this exercise, these are sorted in such a way that the basis functions can be found without using the more cumbersome [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process|"Gram-Schmidt process"]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| + | |||
| + | *For numerical calculations, use $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $ | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
| + | <quiz display=simple> | ||
| + | {In Exercise 4.1, the Gram-Schmidt process resulted in $N = 3$ basis functions. How many basis functions are needed here? | ||
| + | |type="{}"} | ||
| + | $N \ = \ $ { 3 3% } | ||
| + | |||
| + | {Give the 2–norm of all these signals: | ||
| + | |type="{}"} | ||
| + | $||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | $||s_2(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | $||s_3(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | $||s_4(t)|| \ = \ $ { 1.414 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | |||
| + | {Which statements are true for the basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$? | ||
| + | |type="[]"} | ||
| + | + The basis functions computed in "Exericse 4.1" are also appropriate here. | ||
| + | - There are infinitely many possibilities for $\{\varphi_1(t),\ \varphi_2(t),\ \varphi_3(t)\}$. | ||
| + | - A possible set is $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)\}$, with $j = 1,\ 2,\ 3$. | ||
| + | + A possible set is $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, with $j = 1,\ 2,\ 3$. | ||
| + | |||
| + | {What are the coefficients of the signal $s_4(t)$ with respect to the basis functions $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, with $j = 1,\ 2,\ 3$? | ||
| + | |type="{}"} | ||
| + | $s_{\rm 41} \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | $s_{\rm 42} \ = \ $ { -1.03--0.97 } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | $s_{\rm 43} \ = \ $ { 0. } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| + | </quiz> | ||
| + | |||
| + | ===Solution=== | ||
| + | {{ML-Kopf}} | ||
| + | '''(1)''' The only difference to Exercise 4.1 is the different numbering of the signals $s_i(t)$. | ||
| + | *Thus it is obvious that $\underline {N = 3}$ must hold here as well. | ||
| + | |||
| + | |||
| + | '''(2)''' The "2–norm" gives the root of the signal energy and is comparable to the "rms value" for power-limited signals. | ||
| + | *The first three signals all have the same 2–norm: | ||
| + | :$$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *The norm of the last signal is larger by a factor of $\sqrt{2}$: | ||
| + | :$$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' The <u>first and last statements are true</u> in contrast to statements 2 and 3: | ||
| + | * It would be completely illogical if the basis functions found should no longer hold when the signals $s_i(t)$ are sorted differently. | ||
| + | |||
| + | * The Gram–Schmidt process yields only one possible set $\{\varphi_{\it j}(t)\}$ of basis functions. A different sorting (possibly) yields a different basis function. | ||
| + | |||
| + | *The number of permutations of $M = 4$ signals is $4! = 24$. In any case, there cannot be more basis function sets ⇒ solution 2 is wrong. | ||
| + | |||
| + | *However, there are probably $($because of $N = 3)$ only $3! = 6$ possible sets of basis functions. | ||
| + | |||
| + | *As can be seen from the [[Aufgaben:Exercise_4.1:_About_the_Gram-Schmidt_Process|"solution"]] to "Exercise 4.1", the same basis functions will result with the order $s_1(t),\ s_2(t),\ s_4(t),\ s_3(t)$ as with $s_1(t),\ s_2(t),\ s_3(t),\ s_4(t)$. However, this is only a conjecture of the authors; we have not checked it. | ||
| + | |||
| + | * Statement 3 cannot be true simply because of the different units of $s_i(t)$ and $\varphi_{\it j}(t)$. Like $A$, the signals have the unit $\sqrt{\rm W}$, the basis functions the unit $\sqrt{\rm 1/s}$. | ||
| + | |||
| + | * Thus, the last solution is correct, where for $K$ holds: | ||
| + | :$$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$ | ||
| + | '''(4)''' From the comparison of the diagrams in the specification section we can see: | ||
| + | :$$s_{4}(t) = s_{1}(t) - s_{2}(t) = K \cdot \varphi_1(t) - K \cdot \varphi_2(t)\hspace{0.05cm}.$$ | ||
| + | *Furthermore holds: | ||
| + | :$$s_{4}(t) = s_{41}\cdot \varphi_1(t) + s_{42}\cdot \varphi_2(t) + s_{43}\cdot \varphi_3(t)$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}s_{41} = K \hspace{0.1cm}\hspace{0.15cm}\underline {= 10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{42} = -K \hspace{0.1cm}\hspace{0.15cm}\underline {= -10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, | ||
| + | \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 0}\hspace{0.05cm}. $$ | ||
| + | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.1 Basis Functions & Vector Spaces^]] |
Latest revision as of 09:36, 12 August 2022
This exercise pursues exactly the same goal as "Exercise 4.1":
For $M = 4$ energy-limited signals $s_i(t)$ with $i = 1, \ \text{...} \ , 4$, the $N$ required orthonormal basis functions $\varphi_{\it j}(t)$ are to be found, which must satisfy the following condition:
- $$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$
With $M$ transmitted signals $s_i(t)$, already fewer basis functions $\varphi_{\it j}(t)$ can suffice, namely $N$. Thus, in general, $N ≤ M$.
These are exactly the same energy-limited signals $s_i(t)$ as in "Exercise 4.1":
- The difference is the different order of the signals $s_i(t)$.
- In this exercise, these are sorted in such a way that the basis functions can be found without using the more cumbersome "Gram-Schmidt process".
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- For numerical calculations, use $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $
Questions
Solution
- Thus it is obvious that $\underline {N = 3}$ must hold here as well.
(2) The "2–norm" gives the root of the signal energy and is comparable to the "rms value" for power-limited signals.
- The first three signals all have the same 2–norm:
- $$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
- The norm of the last signal is larger by a factor of $\sqrt{2}$:
- $$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
(3) The first and last statements are true in contrast to statements 2 and 3:
- It would be completely illogical if the basis functions found should no longer hold when the signals $s_i(t)$ are sorted differently.
- The Gram–Schmidt process yields only one possible set $\{\varphi_{\it j}(t)\}$ of basis functions. A different sorting (possibly) yields a different basis function.
- The number of permutations of $M = 4$ signals is $4! = 24$. In any case, there cannot be more basis function sets ⇒ solution 2 is wrong.
- However, there are probably $($because of $N = 3)$ only $3! = 6$ possible sets of basis functions.
- As can be seen from the "solution" to "Exercise 4.1", the same basis functions will result with the order $s_1(t),\ s_2(t),\ s_4(t),\ s_3(t)$ as with $s_1(t),\ s_2(t),\ s_3(t),\ s_4(t)$. However, this is only a conjecture of the authors; we have not checked it.
- Statement 3 cannot be true simply because of the different units of $s_i(t)$ and $\varphi_{\it j}(t)$. Like $A$, the signals have the unit $\sqrt{\rm W}$, the basis functions the unit $\sqrt{\rm 1/s}$.
- Thus, the last solution is correct, where for $K$ holds:
- $$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$
(4) From the comparison of the diagrams in the specification section we can see:
- $$s_{4}(t) = s_{1}(t) - s_{2}(t) = K \cdot \varphi_1(t) - K \cdot \varphi_2(t)\hspace{0.05cm}.$$
- Furthermore holds:
- $$s_{4}(t) = s_{41}\cdot \varphi_1(t) + s_{42}\cdot \varphi_2(t) + s_{43}\cdot \varphi_3(t)$$
- $$\Rightarrow \hspace{0.3cm}s_{41} = K \hspace{0.1cm}\hspace{0.15cm}\underline {= 10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{42} = -K \hspace{0.1cm}\hspace{0.15cm}\underline {= -10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 0}\hspace{0.05cm}. $$