Difference between revisions of "Aufgaben:Exercise 1.2: A Simple Binary Channel Code"

From LNTwww
 
(30 intermediate revisions by 5 users not shown)
Line 1: Line 1:
−
{{quiz-Header|Buchseite=Kanalcodierung/Zielsetzung_der_Kanalcodierung
+
{{quiz-Header|Buchseite=Channel_Coding/Objective_of_Channel_Coding
 
}}
 
}}
  
−
[[File:P_ID2381__KC_A_1_2.png|right|frame|Zur Verdeutlichung der Kanalcodierung]]
+
[[File:EN_KC_A_1_2_bitte.png|right|frame|Clarification:  Channel coding and decoding ]]
−
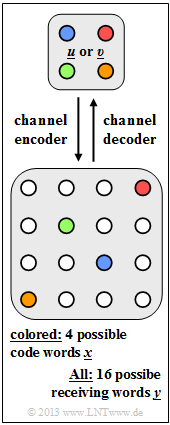
Die Grafik verdeutlicht die hier betrachtete Kanalcodierung C:
+
The graph illustrates the channel coding  $\mathcal{C}$  considered here:
−
*Es gibt vier mögliche Informationsblöcke u = (u_1, u_2, ... , u_k).
+
*There are four possible information blocks  $\underline{u} = (u_{1},\ u_{2},\ \text{...}\hspace{0.05cm} ,\ u_{k})$.
−
*Jeder Informationsblock u wird eindeutig (erkennbar an der gleichen Farbe) dem Codewort x = (x1, x2, ... , xn) zugeordnet.
 
−
*Aufgrund von Decodierfehlern (0 → 1, 1 → 0) gibt es mehr als 4, nämlich 16 verschiedene Empfangsworte y = (y1, y2, ... , yn).
 
−
Ab Teilaufgabe d) betrachten wir folgende Zuordnung:
 
−
   
 
−
''Hinweis:''
 
−
Die hier abgefragten Beschreibungsgrößen wie
 
−
*Coderate,
 
−
*Hamming–Gewicht,
 
−
*Hamming–Distanz, usw.
 
−
werden auf Seite 4 und Seite 5 von Kapitel 1.1 definiert.
 
  
 +
*Each information block  $\underline{u}$  is uniquely assigned  (recognizable by the same color)  to the code word  $\underline{x}= (x_{1},\ x_{2},\ \text{...}\hspace{0.05cm} ,\ x_{n})$ .
  
−
===Fragebogen===
+
*Due to decoding errors  $(0 → 1, \ 1 → 0)$  there are more than 4,  namely 16 different receive words  $\underline{y} = (y_{1},\ y_{2},\ \text{...} \hspace{0.05cm} ,\ y_{n})$.
 +
 
 +
 
 +
From subtask  '''(4)'''  we consider the following mapping:
 +
:$$\underline{u_0} = (0,\ 0) \leftrightarrow (0,\ 0,\ 0,\ 0) = \underline{x_0}\hspace{0.05cm},$$
 +
:$$\underline{u_1} = (0,\ 1) \leftrightarrow (0,\ 1,\ 0,\ 1) = \underline{x_1}\hspace{0.05cm},$$
 +
:$$\underline{u_2} = (1,\ 0) \leftrightarrow (1,\ 0,\ 1,\ 0) = \underline{x_2}\hspace{0.05cm},$$
 +
:$$\underline{u_3} = (1,\ 1) \leftrightarrow (1,\ 1,\ 1,\ 1) = \underline{x_3}\hspace{0.05cm}.$$
 +
 
 +
 
 +
 
 +
Hints:
 +
*This exercise belongs to the chapter  [[Channel_Coding/Objective_of_Channel_Coding|"Objective of Channel Coding"]]
 +
 
 +
*Reference is made in particular to the pages 
 +
:*[[Channel_Coding/Objective_of_Channel_Coding#Block_diagram_and_requirements|"Block diagram and requirements"]],
 +
:*[[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Important definitions for block coding"]].
 +
   
 +
 
 +
 
 +
 
 +
===Questions===
  
 
<quiz display=simple>
 
<quiz display=simple>
−
{Aus wievielen Binärsymbolen besteht ein Informationsblock?
+
{How many binary symbols does an information block consist of?
 
|type="{}"}
 
|type="{}"}
−
$k \ = \ $ { 2 3% }  
+
$k \ = \ $ { 2 }  
  
  
−
{Wie groß ist die Codewortlänge ''n''?
+
{What is the code word length&nbsp; $n$?
 
|type="{}"}
 
|type="{}"}
−
$n \ = \ $ { 4 3% }  
+
$n \ = \ $ { 4 }  
  
−
{Wie groß ist die Coderate?
+
{What is the code rate?
 
|type="{}"}
 
|type="{}"}
 
$R \ = \ $ { 0.5 3% }  
 
$R \ = \ $ { 0.5 3% }  
  
−
{Ist der hier vorgegebene Code systematisch?
+
{Is the code given here systematic?
−
|type="[]"}
+
|type="()"}
−
+ Ja,
+
+ Yes,
−
- Nein.
+
- No.
  
−
{Geben Sie die Hamming–Gewichte aller Codeworte an.
+
{Give the Hamming weights of all code words.
 
|type="{}"}
 
|type="{}"}
−
$ w_{\rm H} \ (\underline{x}_0) \ = \ $ { 0 3 % }
+
$ w_{\rm H} \ (\underline{x}_0) \ = \ $ { 0. }
−
$ w_{\rm H} \ (\underline{x}_1) \ = \ $ { 2 3 % }
+
$ w_{\rm H} \ (\underline{x}_1) \ = \ $ { 2 }
−
$ w_{\rm H} \ (\underline{x}_2) \ = \ $ { 2 3 % }
+
$ w_{\rm H} \ (\underline{x}_2) \ = \ $ { 2 }
−
$ w_{\rm H} \ (\underline{x}_3) \ = \ $ { 4 3 % }
+
$ w_{\rm H} \ (\underline{x}_3) \ = \ $ { 4 }
  
−
{Geben Sie die Hamming–Distanzen zwischen folgenden Codeworten an.
+
{Indicate the Hamming distances between the following code words.
 
|type="{}"}
 
|type="{}"}
−
$ d_{\rm H} \ (\underline{x}_0, \underline{x}_1) \ = \ $ { 2 3 % }
+
$ d_{\rm H} \ (\underline{x}_0,\ \underline{x}_1) \ = \ $ { 2 }
−
$ d_{\rm H} \ (\underline{x}_0, \underline{x}_3) \ = \ $ { 4 3 % }
+
$ d_{\rm H} \ (\underline{x}_0,\ \underline{x}_3) \ = \ $ { 4 }
−
$ d_{\rm H} \ (\underline{x}_1, \underline{x}_2) \ = \ $ { 4 3 % }
+
$ d_{\rm H} \ (\underline{x}_1,\ \underline{x}_2) \ = \ $ { 4 }
  
−
{Wie groß ist die minimale Hamming–Distanz des betrachteten Codes C?
+
{What is the minimum Hamming distance of the code&nbsp; $\mathcal{C}$&nbsp; under consideration?
 
|type="{}"}
 
|type="{}"}
−
$ d_{\rm min} \ (C) \ = \ $ { 2 3 % }
+
$ d_{\rm min} (\mathcal{C}) \ = \ $ { 2 }
  
  
 
</quiz>
 
</quiz>
  
−
===Musterlösung===
+
===Solution===
 
{{ML-Kopf}}
 
{{ML-Kopf}}
−
'''1.'''
+
'''(1)'''&nbsp; The code size here is given to&nbsp; $|\mathcal{C}| = 4$.
−
'''2.'''
+
*In general,&nbsp; $|\mathcal{C}|= 2^k$.
−
'''3.'''
+
*From this follows&nbsp; $\underline{ k = 2}$.
−
'''4.'''
+
 
−
'''5.'''
+
 
−
'''6.'''
+
 
−
'''7.'''
+
'''(2)'''&nbsp; Each code word&nbsp; $\underline{x}$&nbsp; is uniquely associated with an information block&nbsp; $\underline{u}$.
 +
*By corruptions of a single of the total&nbsp; $n$&nbsp; bits of a code word&nbsp; $\underline{x}$&nbsp; the receive words&nbsp; $\underline{y}$&nbsp; result.
 +
*From the number&nbsp; $(16 = 2^4$)&nbsp; of possible receive words follows&nbsp; $\underline{ n = 4}$.
 +
 
 +
 
 +
 
 +
'''(3)'''&nbsp; The code rate is by definition&nbsp; $R = k/n$.&nbsp; Using the above results,&nbsp; we obtain $\underline{R = 0.5}$.
 +
 
 +
 
 +
'''(4)'''&nbsp; Correct is&nbsp; <u>Yes</u>:&nbsp; A systematic code is characterized by the fact that in each case the first&nbsp; $k$&nbsp; bits of the code words are identical to the information block.
 +
 
 +
 
 +
 
 +
'''(5)'''&nbsp; The Hamming weight of a binary code is equal to the algebraic sum&nbsp; $x_1 + x_2 + \text{...} + x_n$&nbsp; over all code word elements.&nbsp; Thus:
 +
:$$w_{\rm H}(\underline{x}_0) \hspace{0.15cm} \underline {= 0} \hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_1) \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}, \hspace{0.3cm} w_{\rm H}(\underline{x}_2) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}.$$
 +
 
 +
 
 +
'''(6)'''&nbsp; The Hamming distance between two code words here can only take the values&nbsp; $2$&nbsp; and&nbsp; $4$:
 +
:$$d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$
 +
 
 +
:$$ d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.$$
 +
 
 +
 
 +
'''(7)'''&nbsp; From the result of subtask&nbsp; '''(6)'''&nbsp; it follows&nbsp; $d_{\rm min}(\mathcal{C}) \hspace{0.15cm}\underline{= 2}$.
 +
*Generally,&nbsp; for this quantity:
 +
:$$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.$$
 +
 
 +
 
 +
 
 
{{ML-Fuß}}
 
{{ML-Fuß}}
  
  
  
−
[[Category:Aufgaben zu  Kanalcodierung|^1.1 Zielsetzung der Kanalcodierung^]]
+
[[Category:Channel Coding: Exercises|^1.1 Objective of Channel Coding^]]

Latest revision as of 15:09, 17 August 2022

Clarification:  Channel coding and decoding

The graph illustrates the channel coding  $\mathcal{C}$  considered here:

  • There are four possible information blocks  $\underline{u} = (u_{1},\ u_{2},\ \text{...}\hspace{0.05cm} ,\ u_{k})$.
  • Each information block  $\underline{u}$  is uniquely assigned  (recognizable by the same color)  to the code word  $\underline{x}= (x_{1},\ x_{2},\ \text{...}\hspace{0.05cm} ,\ x_{n})$ .
  • Due to decoding errors  $(0 → 1, \ 1 → 0)$  there are more than 4,  namely 16 different receive words  $\underline{y} = (y_{1},\ y_{2},\ \text{...} \hspace{0.05cm} ,\ y_{n})$.


From subtask  (4)  we consider the following mapping:

$$\underline{u_0} = (0,\ 0) \leftrightarrow (0,\ 0,\ 0,\ 0) = \underline{x_0}\hspace{0.05cm},$$
$$\underline{u_1} = (0,\ 1) \leftrightarrow (0,\ 1,\ 0,\ 1) = \underline{x_1}\hspace{0.05cm},$$
$$\underline{u_2} = (1,\ 0) \leftrightarrow (1,\ 0,\ 1,\ 0) = \underline{x_2}\hspace{0.05cm},$$
$$\underline{u_3} = (1,\ 1) \leftrightarrow (1,\ 1,\ 1,\ 1) = \underline{x_3}\hspace{0.05cm}.$$


Hints:

  • Reference is made in particular to the pages 



Questions

1

How many binary symbols does an information block consist of?

$k \ = \ $

2

What is the code word length  $n$?

$n \ = \ $

3

What is the code rate?

$R \ = \ $

4

Is the code given here systematic?

Yes,
No.

5

Give the Hamming weights of all code words.

$ w_{\rm H} \ (\underline{x}_0) \ = \ $

$ w_{\rm H} \ (\underline{x}_1) \ = \ $

$ w_{\rm H} \ (\underline{x}_2) \ = \ $

$ w_{\rm H} \ (\underline{x}_3) \ = \ $

6

Indicate the Hamming distances between the following code words.

$ d_{\rm H} \ (\underline{x}_0,\ \underline{x}_1) \ = \ $

$ d_{\rm H} \ (\underline{x}_0,\ \underline{x}_3) \ = \ $

$ d_{\rm H} \ (\underline{x}_1,\ \underline{x}_2) \ = \ $

7

What is the minimum Hamming distance of the code  $\mathcal{C}$  under consideration?

$ d_{\rm min} (\mathcal{C}) \ = \ $


Solution

Solution

(1)  The code size here is given to  $|\mathcal{C}| = 4$.

  • In general,  $|\mathcal{C}|= 2^k$.
  • From this follows  $\underline{ k = 2}$.


(2)  Each code word  $\underline{x}$  is uniquely associated with an information block  $\underline{u}$.

  • By corruptions of a single of the total  $n$  bits of a code word  $\underline{x}$  the receive words  $\underline{y}$  result.
  • From the number  $(16 = 2^4$)  of possible receive words follows  $\underline{ n = 4}$.


(3)  The code rate is by definition  $R = k/n$.  Using the above results,  we obtain $\underline{R = 0.5}$.


(4)  Correct is  Yes:  A systematic code is characterized by the fact that in each case the first  $k$  bits of the code words are identical to the information block.


(5)  The Hamming weight of a binary code is equal to the algebraic sum  $x_1 + x_2 + \text{...} + x_n$  over all code word elements.  Thus:

$$w_{\rm H}(\underline{x}_0) \hspace{0.15cm} \underline {= 0} \hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_1) \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}, \hspace{0.3cm} w_{\rm H}(\underline{x}_2) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm}w_{\rm H}(\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}.$$


(6)  The Hamming distance between two code words here can only take the values  $2$  and  $4$:

$$d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_1) \hspace{0.15cm} \underline {= 2}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_2) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_0, \hspace{0.05cm}\underline{x}_3) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$
$$ d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_2) \hspace{0.15cm} \underline {= 4}\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_1, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{x}_2, \hspace{0.05cm}\underline{x}_3) = 2\hspace{0.05cm}.$$


(7)  From the result of subtask  (6)  it follows  $d_{\rm min}(\mathcal{C}) \hspace{0.15cm}\underline{= 2}$.

  • Generally,  for this quantity:
$$d_{\rm min}(\mathcal{C}) = \min_{\substack{\underline{x},\hspace{0.05cm}\underline{x}' \hspace{0.05cm}\in \hspace{0.05cm} \mathcal{C} \ {\underline{x}} \hspace{0.05cm}\ne \hspace{0.05cm} \underline{x}'}}\hspace{0.1cm}d_{\rm H}(\underline{x}, \hspace{0.05cm}\underline{x}')\hspace{0.05cm}.$$


Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_1.2:_A_Simple_Binary_Channel_Code&oldid=48419"
  • Powered by MediaWiki