Aufgaben:Exercise 2.2Z: Galois Field GF(5)

• Return to book

Addition/multiplication for  $\{a, \, b, \, c, \, d, \, e\}$

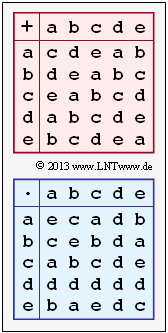
As in the  Exercise 2.2  we consider a finite field of order  $q = 5$  and thus the Galois field

$${\rm GF}(5) = \{{a}, { b},{c},{d},{e}\}\hspace{0.05cm}.$$

No further statements are made about the elements. They can be integers or any mathematical expressions.

The Galois field is determined exclusively by

• an addition table modulo 5,
• a multiplication table modulo 5,

The main properties of a Galois field are compiled on the  "first theory page" . Here reference is made to

• the commutative and distributive laws,
• the neutral elements of addition and multiplication,
• the inverse elements of addition and multiplication, and
• the determination of primitive elements.

In the present example  $\beta$  would be a primitive element if  $\beta^2, \ \beta^3$  and  $\beta^4$  (in general:  $\beta^{q-1})$  yield the remaining elements of the Galois field  $\rm GF(5)$  except for the zero element.

Hints:

• The exercise is related to the topic of the chapter "Some Basics of Algebra".
• Please don't be confused that in the text the set  $ \{{a}, { b},{c},{d},{e}\}$  is used and in the tables the set  $ \rm \{{a}, { b},{c},{d},{e}\}$. Apologies.

Questions

1

Determine the neutral element of addition.

	$N_{\rm A} = a$,
	$N_{\rm A} = b$,
	$N_{\rm A} = c$,
	$N_{\rm A} = d$,
	$N_{\rm A} = e$.

2

Determine the neutral element of multiplication.

	$N_{\rm M} = a$,
	$N_{\rm M} = b$,
	$N_{\rm M} = c$,
	$N_{\rm M} = d$,
	$N_{\rm M} = e$.

3

If the commutative law is satisfied,

	with respect to addition, for example  $a + b = b + a, \hspace{0.05cm}\text{ ...} \hspace{0.1cm}, \ d + e = e + d$,
	with respect to multiplication, for example  $a \cdot b = b \cdot a, \hspace{0.05cm}\text{ ...} \hspace{0.1cm}, \ d \cdot e = e \cdot d$.

4

For which expressions is the distributive law satisfied?

	$a \cdot (b + c) = a \cdot b + a \cdot c$,
	$d \cdot (b + c) = d \cdot b + d \cdot c$,
	$e \cdot (a + b) = e \cdot a + e \cdot b$.

5

Replace  $a, \ b, \ c, \ d, \ e$  with elements of the number set  $\{0, \, 1, \, 2, \, 3, \, 4\}$ so that equal operation tables result.

$a \hspace{0.2cm} = \ $

$b \hspace{0.25cm} = \ $

$c \hspace{0.25cm} = \ $

$d \hspace{0.2cm} = \ $

$e \hspace{0.2cm} = \ $

6

What statements are true regarding inverse elements?

	For all  $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$  there is an additive inverse.
	Only for  $z_i ∈ \{1, \, 2, \, 3, \, 4\}$  there is an additive inverse.
	For all  $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$  there is a multiplicative inverse.
	Only for  $z_i ∈ \{1, \, 2, \, 3, \, 4\}$  there is a multiplicative inverse.

7

Which of the elements are primitive?

	$a = 3$.
	$b = 2$,
	$e = 4$.

Solution

Solution

(1)  The neutral element with respect to addition (called $N_{\rm A}$) must satisfy the following equation for all elements $z_i (i = 0, \hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$:

$$z_i + N_{\rm A} = N_{\rm A} + z_i = z_i\hspace{0.05cm}.$$

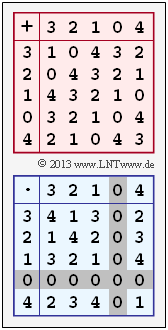
From the addition table it follows $N_{\rm A} \ \underline{= d}$.

(2)  In contrast, for all elements $z_i (i = 1,\hspace{0.05cm}\text{ ...} \hspace{0.1cm} , \ q-1)$, the neutral element of multiplication $(N_{\rm M})$ satisfies the following condition:

$$z_i \cdot N_{\rm M} = N_{\rm M}\cdot z_i = z_i\hspace{0.05cm}.$$

From the multiplication table, one can see $N_{\rm M} \ \underline{= c}$.

(3)  The commutative law is satisfied for this Galois field in both cases (addition and multiplication), since the addition table and multiplication table are each symmetric about the table diagonal.

(4)  Let us first consider the first expression. If the distributive law is valid, it must hold:

$$a \cdot (b+c) = a \cdot b+ a \cdot c \hspace{0.05cm}.$$

For the left side you get:

$$a \cdot (b+c) = a \cdot a =e \hspace{0.05cm},$$

and for the right side:

$$a \cdot b+ a \cdot c = c + a = e\hspace{0.05cm}.$$

The distributive law is satisfied here as well as for the other two given expressions:

$$d \cdot (b+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot a =d \hspace{0.05cm}, \hspace{0.5cm}d \cdot b+ d \cdot c = d + d = d\hspace{0.05cm},$$

$$e \cdot (a+c) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} e \cdot e =c \hspace{0.05cm}, \hspace{0.5cm}e \cdot a+ e \cdot c = b + e = c\hspace{0.05cm}.$$

All proposed solutions apply.

Transformed operation tables

(5)  The zero element  $N_{\rm A} = d$  becomes  $N_{\rm A} = 0 \Rightarrow d = 0$, the identity element  $N_{\rm M} = c$  becomes $N_{\rm M} = 1 \Rightarrow c = 1$. The other elements  $a, \ b$  and  $e$  can be determined modulo  $5$  from the addition table or the multiplication table. For example, from the first row of the addition table follows

$$(a + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = d = 0 \hspace{0.05cm}.$$

Since both  $a$  and  $b$  cannot be  $0$  or  $1$  (since these are already assigned for  $c$  and  $d$  ), the inference is:

$$a = 2, \hspace{0.1cm} b = 3 \hspace{0.5cm}{\rm oder}\hspace{0.5cm} a = 3, \hspace{0.1cm} b = 2\hspace{0.05cm}.$$

For example, from the second row of the addition table it follows:

$$(b + b) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = e \hspace{0.05cm}.$$

From  $b = 3$  would result  $e = 1$. But this is again not possible, because already  $c = 1$  has been defined.

So you get as a final result:

$$a \hspace{0.15cm}\underline{= 3}\hspace{0.05cm},\hspace{0.2cm}b \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},\hspace{0.2cm} c \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},\hspace{0.2cm}d \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm} e \hspace{0.15cm}\underline{= 4}\hspace{0.05cm}.$$

The graph shows the addition and multiplication table for this set of numbers.

(6)  True are statements 1 and 4:

• In the addition table, one recognizes exactly one  $d = 0$ in each row and column. That is,   For all  $z_i ∈ \{0, \, 1, \, 2, \, 3, \, 4\}$  there exists a unique additive inverse.

The multiplicative inverse can be recognized in the multiplication table by the entry  $c = 1$. The multiplicative inverses are as follows:

$${\rm Zeile \hspace{0.15cm}1\text{:}}\hspace{0.25cm} {\rm Inv_M}(a=3) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} b = 2 \hspace{0.05cm},$$

$${\rm Zeile\hspace{0.15cm} 2\text{:}}\hspace{0.25cm} {\rm Inv_M}(b=2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} a=3 \hspace{0.05cm},$$

$${\rm Zeile\hspace{0.15cm} 3\text{:}}\hspace{0.25cm} {\rm Inv_M}(c=1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} c=1 \hspace{0.05cm},$$

$${\rm Zeile\hspace{0.15cm} 5\text{:}}\hspace{0.25cm} {\rm Inv_M}(e=4) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} e=4 \hspace{0.05cm}.$$

For the zero element  $d = 0$  on the other hand, no multiplicative inverse exists.

(7)  Concerning the primitive elements one obtains

$$a \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 3 \hspace{0.05cm},\hspace{0.2cm} a^2 = 9 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},\hspace{0.2cm} a^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} a^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$

$$b \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 2 \hspace{0.05cm},\hspace{0.2cm} b^2 = 4 \hspace{0.05cm},\hspace{0.2cm} b^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} b^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm primitiv}\hspace{0.05cm},$$

$$e \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 4 \hspace{0.05cm},\hspace{0.2cm} e^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},\hspace{0.2cm} e^3 = \hspace{0.05cm} ...\hspace{0.05cm}= 4\hspace{0.05cm},\hspace{0.2cm} e^4 =\hspace{0.05cm} ...\hspace{0.05cm} = 1\hspace{0.13cm} \Rightarrow \hspace{0.13cm}{\rm nicht\hspace{0.15cm} primitiv}\hspace{0.05cm}.$$

From the set $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\}$, "$2$" and "$3$" are primitive elements  ⇒  solution suggestions 1 and 2.