Difference between revisions of "Aufgaben:Exercise 2.1: Group, Ring, Field"
| (29 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Some_Basics_of_Algebra}} |
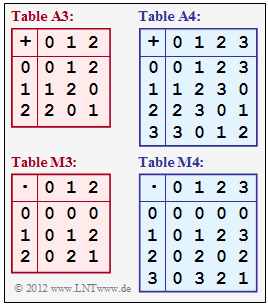
| − | [[File: | + | [[File:EN_KC_A_2_1.png|right|frame|"Addition" and "Multiplication" <br> for $q = 3$ and $q = 4$.]] |
| − | + | In the [[Channel_Coding/Some_Basics_of_Algebra|"theory section"]] to this chapter, various algebraic terms were defined. For what follows, we assume that all sets consist of $q$ elements each, where here either $q = 3$ or $q = 4$. Then holds: | |
| − | * | + | * An [[Channel_Coding/Some_Basics_of_Algebra#Definition_and_examples_of_an_algebraic_group|"algebraic group"]] is a finite set $G = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$ together with a linking rule defined between all elements. An "additive group" is denoted by $(G, \ +)$, a multiplicative one by $(G, \ \cdot)$. |
| − | * | + | * An [[Channel_Coding/Some_Basics_of_Algebra#Definition_and_examples_of_an_algebraic_ring|"algebraic ring"]] denotes a set $R = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$ together with two arithmetic operations defined therein, namely addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$"). |
| − | * | + | * An [[Channel_Coding/Some_Basics_of_Algebra#Group.2C_ring.2C_field_-_basic_algebraic_concepts|"algebraic field"]] is a ring where division is additionally allowed and the commutative law is satisfied. |
| − | + | Since we consider here finite sets only, a "field" is at the same time a [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"Galois field"]] ${\rm GF}(q)$ of order $q$. | |
| − | + | An essential property of the Galois field ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm}\text{...} \hspace{0.1cm} , \hspace{0.1cm}z_{q-1}\}$ is that it has at least one primitive element: An element $z_i ≠ 0$ is said to be "primitive" if the following condition is satisfied $(k$ is an integer$)$: | |
| − | |||
| − | |||
| − | |||
:$$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ | :$$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ | ||
1 \end{array} \right.\quad | 1 \end{array} \right.\quad | ||
| − | \begin{array}{*{1}c} {\rm | + | \begin{array}{*{1}c} {\rm for} \hspace{0.15cm}1 \le k < q-1 |
| − | \\ {\rm | + | \\ {\rm for} \hspace{0.15cm}k = q-1 \\ \end{array} |
| − | \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm | + | \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm is \hspace{0.15cm}a\hspace{0.15cm} primitive \hspace{0.15cm}element} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | Only for a primitive element $z_i$ | |
| + | *the arithmetic oparation $z_i^k$ $($with $k = 1, \, 2, \, 3, \, \hspace{0.05cm}\text{...} )$ yields all elements of the Galois field | ||
| + | *except the zero element $z_0 = 0$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | * The exercise covers the topic of the chapter [[Channel_Coding/Some_Basics_of_Algebra| "Some basics of algebra"]]. | ||
| − | + | * Note that for group, ring and field with each $q$ elements, the arithmetic operations "$+$" and "$\hspace{0.05cm}\cdot\hspace{0.05cm}$" are to be understood modulo $q$. | |
| − | * | ||
| − | |||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the given tables describe a '''group'''? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + Table $\rm A3$, |
| − | - | + | + Table $\rm M3$, |
| + | - Table $\rm A3$ and table $\rm M3$ together, | ||
| + | - Table $\rm A4$ and table $\rm M4$ together. | ||
| − | { | + | {Which of the given tables describe a '''ring'''? |
| − | |type="{}"} | + | |type="[]"} |
| − | $ | + | - Table $\rm A3$, |
| + | - Table $\rm M3$, | ||
| + | + Table $\rm A3$ and table $\rm M3$ together, | ||
| + | + table $\rm A4$ and table $\rm M4$ together, | ||
| + | - Table $\rm A3$ and table $\rm M4$ together. | ||
| + | |||
| + | {Which of the tables describe a '''(Galois) field'''? | ||
| + | |type="[]"} | ||
| + | - Table $\rm A3$, | ||
| + | - Table $\rm M3$, | ||
| + | + Table $\rm A3$ and table $\rm M3$ together, | ||
| + | - Table $\rm A4$ and table $\rm M4$ together. | ||
| + | |||
| + | {Which elements of the set $\{0, \, 1, \, 2\} \ \Rightarrow \ q = 3$ are "primitive"? | ||
| + | |type="[]"} | ||
| + | - $z_0 = 0$, | ||
| + | - $z_1 = 1$, | ||
| + | + $z_2 = 2.$ | ||
| + | |||
| + | {Which elements of the set $\{0, \, 1, \, 2, \, 3\} \ \Rightarrow \ q = 4$ are "primitive"? | ||
| + | |type="[]"} | ||
| + | - $z_0 = 0$, | ||
| + | - $z_1 = 1$, | ||
| + | - $z_2 = 2$, | ||
| + | - $z_3 = 3$. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With the number set $Z_3 = \{0, \, 1, \, 2\}$ describes |
| − | '''(2)''' | + | * the table A3 the additive group $(Z_3, \, +)$, |
| − | '''(3)''' | + | * the table M3 the multiplicative group $(Z_3, \, \cdot)$. |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| + | ⇒ <u>Solution suggestion 1 and 2</u>. | ||
| + | |||
| + | The solution suggestions 3 and 4 do not apply here, because only one arithmetic operation (addition or multiplication) is defined for each group. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' On an algebraic ring, in contrast, two arithmetic operations are defined. Thus, the <u>proposed solutions 3 and 4</u> are correct: | ||
| + | * Tables A3 and M3 describe together the ring $(Z_3, \, +, \, \cdot)$. | ||
| + | * Tables A4 and M4 describe together the ring $(Z_4, \, +, \, \cdot)$. | ||
| + | |||
| + | |||
| + | In contrast, A3 and M4 do not describe a ring because they refer to different quantities. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Every field is also a ring, but not every ring is also a field: | ||
| + | *For the latter, division is also defined and for each element there is also the '''multiplicative inverse'''. | ||
| + | *A '''finite number ring''' of order $q$ (that is, with $q$ elements) is a field only if $q$ is a prime number. | ||
| + | *This is then also called a '''Galois field''' ${\rm GF}(q)$. | ||
| + | |||
| + | |||
| + | So the correct answer is <u>answer 3</u>: | ||
| + | *The arithmetic operations according to tables A3 and M3 together result in the Galois field ${\rm GF}(3)$. | ||
| + | *In contrast, tables A4 (addition) and M4 multiplication) together with the set $\{0, \, 1, \, 2, \, 3\}$ do not result in the Galois field ${\rm GF}(4)$. | ||
| + | *A condition for a Galois field is that for each element $z_i$ there exists a multiplicative inverse ${\rm Inv}_{\rm M}{(z_i)}$ such that the equation $z_i \cdot {\rm Inv}_{\rm M}(z_i) = 1$ is satisfied. | ||
| + | *According to table M4, however, $\rm Inv_M(2)$ does not exist. There is no "$1$" in the third row. | ||
| + | |||
| + | |||
| + | For example, a Galois field $\rm GF(4)$ is obtained by extending the binary set $\{0, \, 1\}$ to the set $\{0, \, 1, \, \alpha, \, 1+\alpha\}$. For more details, see the page [[Channel_Coding/Extension_Field#GF.2822.29_.E2.80.93_Example_of_an_extension.C3.B6rpers|"Example of an extension field"]] page. | ||
| + | |||
| + | |||
| + | '''(4)''' The zero element is never a primitive element. Also $z_1 = 1$ is not a primitive element, because then with $q = 3$ would have to hold: | ||
| + | :$$z_1^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} \ne 1 \hspace{0.05cm},\hspace{0.3cm}z_1^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | On the other hand, $z_2 = 2$ is a primitive element because of | ||
| + | |||
| + | :$$2^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 2 \hspace{0.05cm},\hspace{0.3cm}2^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | The correct solution is <u>solution suggestion 3</u>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' The set $\{0, \, 1, \, 2, \, 3\}$ has <u>no primitive element</u> and accordingly does not satisfy the requirements of a Galois field: | ||
| + | :$$z_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\text{:}\hspace{0.35cm} 1^1 = 1\hspace{0.05cm},\hspace{0.1cm}1^2 = 1\hspace{0.05cm},\hspace{0.1cm}1^3 = 1\hspace{0.05cm},$$ | ||
| + | :$$z_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\text{:}\hspace{0.35cm} 2^1 = 2\hspace{0.05cm},\hspace{0.1cm}2^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0 \hspace{0.05cm},\hspace{0.1cm}2^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0\hspace{0.05cm},$$ | ||
| + | :$$z_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\text{:}\hspace{0.35cm} 3^1 = 3\hspace{0.05cm},\hspace{0.1cm}3^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 1 \hspace{0.05cm},\hspace{0.1cm}3^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 3\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.1 Some Basics of Algebra^]] |
Latest revision as of 14:17, 27 August 2022
In the "theory section" to this chapter, various algebraic terms were defined. For what follows, we assume that all sets consist of $q$ elements each, where here either $q = 3$ or $q = 4$. Then holds:
- An "algebraic group" is a finite set $G = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$ together with a linking rule defined between all elements. An "additive group" is denoted by $(G, \ +)$, a multiplicative one by $(G, \ \cdot)$.
- An "algebraic ring" denotes a set $R = \{0, \, 1, \hspace{0.05cm}\text{...} \hspace{0.1cm} , \ q-1\}$ together with two arithmetic operations defined therein, namely addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$").
- An "algebraic field" is a ring where division is additionally allowed and the commutative law is satisfied.
Since we consider here finite sets only, a "field" is at the same time a "Galois field" ${\rm GF}(q)$ of order $q$.
An essential property of the Galois field ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm}\text{...} \hspace{0.1cm} , \hspace{0.1cm}z_{q-1}\}$ is that it has at least one primitive element: An element $z_i ≠ 0$ is said to be "primitive" if the following condition is satisfied $(k$ is an integer$)$:
- $$z_i^k \hspace{0.15cm}{\rm mod}\hspace{0.15cm}q = \left\{ \begin{array}{c} \ne 1\\ 1 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for} \hspace{0.15cm}1 \le k < q-1 \\ {\rm for} \hspace{0.15cm}k = q-1 \\ \end{array} \hspace{0.35cm} \Rightarrow \hspace{0.35cm} z_i \hspace{0.15cm}{\rm is \hspace{0.15cm}a\hspace{0.15cm} primitive \hspace{0.15cm}element} \hspace{0.05cm}. $$
Only for a primitive element $z_i$
- the arithmetic oparation $z_i^k$ $($with $k = 1, \, 2, \, 3, \, \hspace{0.05cm}\text{...} )$ yields all elements of the Galois field
- except the zero element $z_0 = 0$.
Hints:
- The exercise covers the topic of the chapter "Some basics of algebra".
- Note that for group, ring and field with each $q$ elements, the arithmetic operations "$+$" and "$\hspace{0.05cm}\cdot\hspace{0.05cm}$" are to be understood modulo $q$.
Questions
Solution
- the table A3 the additive group $(Z_3, \, +)$,
- the table M3 the multiplicative group $(Z_3, \, \cdot)$.
⇒ Solution suggestion 1 and 2.
The solution suggestions 3 and 4 do not apply here, because only one arithmetic operation (addition or multiplication) is defined for each group.
(2) On an algebraic ring, in contrast, two arithmetic operations are defined. Thus, the proposed solutions 3 and 4 are correct:
- Tables A3 and M3 describe together the ring $(Z_3, \, +, \, \cdot)$.
- Tables A4 and M4 describe together the ring $(Z_4, \, +, \, \cdot)$.
In contrast, A3 and M4 do not describe a ring because they refer to different quantities.
(3) Every field is also a ring, but not every ring is also a field:
- For the latter, division is also defined and for each element there is also the multiplicative inverse.
- A finite number ring of order $q$ (that is, with $q$ elements) is a field only if $q$ is a prime number.
- This is then also called a Galois field ${\rm GF}(q)$.
So the correct answer is answer 3:
- The arithmetic operations according to tables A3 and M3 together result in the Galois field ${\rm GF}(3)$.
- In contrast, tables A4 (addition) and M4 multiplication) together with the set $\{0, \, 1, \, 2, \, 3\}$ do not result in the Galois field ${\rm GF}(4)$.
- A condition for a Galois field is that for each element $z_i$ there exists a multiplicative inverse ${\rm Inv}_{\rm M}{(z_i)}$ such that the equation $z_i \cdot {\rm Inv}_{\rm M}(z_i) = 1$ is satisfied.
- According to table M4, however, $\rm Inv_M(2)$ does not exist. There is no "$1$" in the third row.
For example, a Galois field $\rm GF(4)$ is obtained by extending the binary set $\{0, \, 1\}$ to the set $\{0, \, 1, \, \alpha, \, 1+\alpha\}$. For more details, see the page "Example of an extension field" page.
(4) The zero element is never a primitive element. Also $z_1 = 1$ is not a primitive element, because then with $q = 3$ would have to hold:
- $$z_1^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} \ne 1 \hspace{0.05cm},\hspace{0.3cm}z_1^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 \hspace{0.05cm}.$$
On the other hand, $z_2 = 2$ is a primitive element because of
- $$2^1 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 2 \hspace{0.05cm},\hspace{0.3cm}2^2 \hspace{0.15cm}{\rm mod\hspace{0.15cm}} 3\hspace{0.1cm} = 1 \hspace{0.05cm}.$$
The correct solution is solution suggestion 3.
(5) The set $\{0, \, 1, \, 2, \, 3\}$ has no primitive element and accordingly does not satisfy the requirements of a Galois field:
- $$z_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\text{:}\hspace{0.35cm} 1^1 = 1\hspace{0.05cm},\hspace{0.1cm}1^2 = 1\hspace{0.05cm},\hspace{0.1cm}1^3 = 1\hspace{0.05cm},$$
- $$z_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\text{:}\hspace{0.35cm} 2^1 = 2\hspace{0.05cm},\hspace{0.1cm}2^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0 \hspace{0.05cm},\hspace{0.1cm}2^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 0\hspace{0.05cm},$$
- $$z_3 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\text{:}\hspace{0.35cm} 3^1 = 3\hspace{0.05cm},\hspace{0.1cm}3^2 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 1 \hspace{0.05cm},\hspace{0.1cm}3^3 \hspace{0.15cm}{\rm mod}\hspace{0.15cm}4 = 3\hspace{0.05cm}.$$