Aufgaben:Exercise 4.17Z: Rayleigh and Rice Distribution

• Return to book

Rice (top) and Rayleigh (bottom)

For the study of transmission systems,  the Rayleigh and Rice distributions are of great importance.  In the following let  $y$  be a Rayleigh or a Rice distributed random variable and  $\eta$  in each case a realization of it.

• The  "Rayleigh distribution"  results thereby for the probability density function  $\rm (PDF)$  of a random variable  $y$,  which results from the two Gaussian distributed and statistically independent components  $u$  and  $v$  $($both with the standard deviation  $\sigma_n)$  as follows:

$$y = \sqrt{u^2 + v^2} \hspace{0.1cm} \Rightarrow \hspace{0.1cm} p_y (\eta) = \frac{\eta}{\sigma_n^2} \cdot {\rm exp } \left [ - \frac{\eta^2}{2 \sigma_n^2}\right ] \hspace{0.01cm}.$$

• The  "Rice distribution"  is obtained under otherwise identical boundary conditions for the application case where a constant  $C$  is still added to one of the two components,  for example:

$$y = \sqrt{(u+C)^2 + v^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_y (\eta) = \frac{\eta}{\sigma_n^2} \cdot {\rm exp } \left [ - \frac{\eta^2 + C^2}{2 \sigma_n^2}\right ] \cdot {\rm I }_0 \left [ \frac{\eta \cdot C}{ \sigma_n^2}\right ] \hspace{0.05cm}.$$

In this equation,  ${\rm I}_0(x)$  denotes the  "modified zero-order Bessel function".

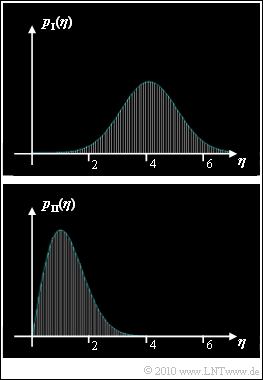
In the graph,  the two probability density functions are shown,  but it is not indicated whether  $p_{\hspace{0.03cm}\rm I}(\eta)$  or  $p_{\hspace{0.03cm}\rm II}(\eta)$  belong to a Rayleigh or a Rice distribution,  respectively.

• It is only known that one Rayleigh and one Rice distribution is shown.

• The parameter  $\sigma_n$  is the same for both distributions.

For your decision whether to assign  $p_{\hspace{0.03cm}\rm I}(\eta)$  or  $p_{\rm II}(\hspace{0.03cm}\eta)$  to the Rice distribution and for the determination of the PDF parameters you can consider the following statements:

• For large values of the quotient  $C/\sigma_n$,  the Rice distribution can be approximated by a Gaussian distribution with mean  $C$  and standard deviation  $\sigma_n$. 

• The values of  $C$  and  $\sigma_n$  underlying the graph are integers.

Regarding the Rayleigh distribution,  note:

• The same  $\sigma_n$  is used for both distributions.

• For the standard deviation  (root of the variance)  of the Rayleigh distribution holds:

$$\sigma_y = \sigma_n \cdot \sqrt{2 - {\pi}/{2 }} \hspace{0.2cm} \approx \hspace{0.2cm} 0.655 \cdot \sigma_n \hspace{0.05cm}.$$

• For the standard deviation or for the variance of the Rice distribution in general only a complicated expression with hypergeometric functions can be given,  otherwise only an approximation for  $C \gg \sigma_n$  corresponding to the Gaussian distribution.

Notes:

• This exercise belongs to the chapter  "Carrier Frequency Systems with Non-Coherent Demodulation".

• Given is also the following indefinite integral:

$$\int x \cdot {\rm e }^{-x^2} \,{\rm d} x = -{1}/{2} \cdot {\rm e }^{-x^2} + {\rm const. }$$

Questions

1

Assign the graphs to the Rayleigh and Rice distributions, respectively.

	$p_{\hspace{0.03cm}\rm I}(\eta)$  corresponds to the Rayleigh distribution,  $p_{\hspace{0.03cm}\rm II}(\eta)$  to the Rice distribution.
	$p_{\hspace{0.03cm}\rm I}(\eta)$  corresponds to the Rice distribution,  $p_{\hspace{0.03cm}\rm II}(\eta)$  to the Rayleigh distribution.

2

Give the parameters of the Rice distribution shown here.

$C \hspace{0.25cm} = \ $

$\sigma_n \ = \ $

3

Which distribution has a larger variance?

	The Rayleigh distribution,
	the Rice distribution?

4

Calculate the excess probabilities of the Rayleigh distribution.

${\rm Pr}(y > \sigma_n) \hspace{0.33cm} = \ $ $\ \%$

${\rm Pr}(y > 2\sigma_n) \ = \ $ $\ \%$

${\rm Pr}(y > 3\sigma_n) \ = \ $ $\ \%$

Solution

Solution

(1)  The  second solution  is correct:

• The upper graph shows approximately a Gaussian distribution and belongs accordingly to the Rice distribution.

(2)  You can see from the graph:  The mean value of the Gaussian distribution is  $\underline {C = 4}$ and the standard deviation is $\underline {\sigma_n = 1}$.

• It was given that  $C$  and  $\sigma_n$  were integers.  Thus the two density functions are:

$$p_{\rm I} (\eta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\eta} \cdot {\rm exp } \left [ - \frac{\eta^2 + 16}{2 }\right ] \cdot {\rm I }_0 (4\eta ) \approx \frac{1}{\sqrt{2\pi }}\cdot {\rm exp } \left [ - \frac{(\eta-4)^2 }{2 }\right ]\hspace{0.05cm},$$

$$p_{\rm II} (\eta) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\eta} \cdot {\rm exp } \left [ - \frac{\eta^2 }{2 }\right ] \hspace{0.05cm}.$$

(3)  Solution 2  is correct,  as can already be seen from the graph.  A calculation confirms this result:

$$\sigma_{\rm Rice}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sigma_n^2 = 1\hspace{0.05cm},$$

$$\sigma_{\rm Rayl}^2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sigma_n^2 \cdot ({2 - {\pi}/{2 }}) \approx 0.429 \hspace{0.05cm}.$$

(4)  In general,  the probability that  $y$  is greater than a certain value  $y_0$  is equal to

$${\rm Pr}(y > y_0) = \int_{y_0}^{\infty} \frac{\eta}{\sigma_n^2} \cdot {\rm exp } \left [ - \frac{\eta^2 }{2 \sigma_n^2}\right ] \,{\rm d} \eta \hspace{0.05cm}.$$

• With the substitution  $x^2 = \eta^2/(2\sigma_n^2)$  can be written for this:

$${\rm Pr}(y > y_0) = 2 \cdot \hspace{-0.05cm}\int_{y_0/(\sqrt{2}\hspace{0.03cm} \cdot \hspace{0.03cm} \sigma_n)}^{\infty} \hspace{-0.5cm}x \cdot {\rm e }^{ - x^2} \,{\rm d} x = \left [{\rm e }^{ - x^2} \right ]_{\sqrt{2}\hspace{0.03cm} \cdot \hspace{0.03cm} \sigma_n}^{\infty} = {\rm exp } \left [ -\frac{ y_0^2 }{2 \sigma_n^2 }\right ]\hspace{0.05cm}.$$

• Here the indefinite integral given in the front was used.  In particular:

$${\rm Pr}(y > \sigma_n) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{ - 0.5} \hspace{0.15cm} \underline{\approx 60.7 \%} \hspace{0.05cm},$$

$${\rm Pr}(y > 2\sigma_n) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{ - 2.0} \hspace{0.15cm} \underline{\approx 13.5 \%} \hspace{0.05cm},$$

$${\rm Pr}(y > 3\sigma_n) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {\rm e }^{ - 4.5} \hspace{0.15cm} \underline{\approx 1.1 \%} \hspace{0.05cm}.$$