Difference between revisions of "Aufgaben:Exercise 1.4: Rayleigh PDF and Jakes PDS"
| (17 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process}} |
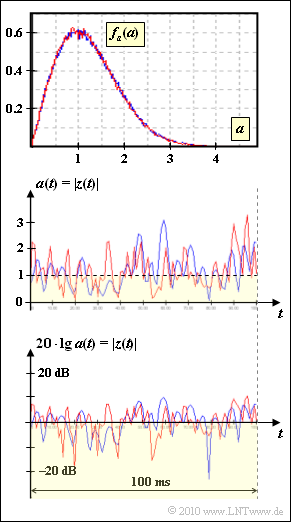
| − | [[File:P_ID2119__Mob_A_1_4.png|right|frame| PDF and $|z(t)|$ for Rayleigh | + | [[File:P_ID2119__Mob_A_1_4.png|right|frame| PDF and $|z(t)|$ for Rayleigh fading with Doppler effect]] |
We consider two different mobile radio channels with [[Mobile_Communications/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Beispielhafte_Signalverl.C3.A4ufe_bei_Rayleigh.E2.80.93Fading|Rayleigh fading]]. In both cases the PDF of the magnitude $a(t) = |z(t)| ≥ 0$ is | We consider two different mobile radio channels with [[Mobile_Communications/Wahrscheinlichkeitsdichte_des_Rayleigh%E2%80%93Fadings#Beispielhafte_Signalverl.C3.A4ufe_bei_Rayleigh.E2.80.93Fading|Rayleigh fading]]. In both cases the PDF of the magnitude $a(t) = |z(t)| ≥ 0$ is | ||
:$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} | :$$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The probability that this | + | The probability that this magnitude is not greater than a given value $A$ is |
:$${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} | :$${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The two channels, which are designated according to the colors | + | The two channels, which are designated according to the colors "Red" and "Blue" in the graphs with $\rm R$ and $\rm B$ respectively, differ in the speed $v$ and thus in the form of the power-spectral density $\rm (PSD)$ ${\it \Phi}_z(f_{\rm D})$. |
| − | *In both cases, however, the | + | *In both cases, however, the PDS is a [[Mobile_Communications/Statistical_bindings_within_the_Rayleigh_process|Jakes spectrum]]. |
| − | *For a Doppler frequency $f_{\rm D}$ with $|f_{\rm D}| <f_{\rm D,\hspace{0. | + | *For a Doppler frequency $f_{\rm D}$ with $|f_{\rm D}| <f_{\rm D,\hspace{0.1cm}max}$ the Jakes spectrum is given by |
| − | :$${\it \ | + | :$${\it \Phi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.1cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.1cm} max})^2} } |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *For Doppler frequencies outside this interval from $-f_{\rm D,\hspace{0. | + | *For Doppler frequencies outside this interval from $-f_{\rm D,\hspace{0.1cm}max}$ to $+f_{\rm D,\hspace{0.1cm}max}$, we have ${\it \Phi}_z(f_{\rm D})=0$. |
| − | The corresponding descriptor in the time domain is the | + | The corresponding descriptor in the time domain is the auto-correlation function $\rm (ACF)$: |
| − | :$$\varphi_z ({\rm \delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0. | + | :$$\varphi_z ({\rm \delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot {\rm \delta}t)\hspace{0.05cm}.$$ |
| − | *Here, ${\rm J_0}(.)$ is the | + | *Here, ${\rm J_0}(.)$ is the Bessel function of the first kind and zeroth order. We have ${\rm J_0}(0) = 1$. |
| − | *The maximum Doppler frequency of the channel model $\rm R$ | + | *The maximum Doppler frequency of the channel model $\rm R$ is known to be $f_{\rm D,\hspace{0.1cm}max} = 200 \ \rm Hz$. |
* It is also known that the speeds $v_{\rm R}$ and $v_{\rm B}$ differ by the factor $2$ . | * It is also known that the speeds $v_{\rm R}$ and $v_{\rm B}$ differ by the factor $2$ . | ||
*Whether $v_{\rm R}$ is twice as large as $v_{\rm B}$ or vice versa, you should decide based on the above graphs. | *Whether $v_{\rm R}$ is twice as large as $v_{\rm B}$ or vice versa, you should decide based on the above graphs. | ||
| Line 37: | Line 37: | ||
''Notes:'' | ''Notes:'' | ||
| − | * This task belongs to the topic of [[Mobile_Communications/ | + | * This task belongs to the topic of [[Mobile_Communications/Statistical_Bindings_within_the_Rayleigh_Process#ACF_and_PDS_with_Rayleigh.E2.80.93Fading|Statistical bindings within the Rayleigh process]]. |
* To check your results you can use the interactive applet [[Applets:PDF,_CDF_and_Moments_of_Special_Distributions|PDF, CDF and Moments of Special Distributions]]. | * To check your results you can use the interactive applet [[Applets:PDF,_CDF_and_Moments_of_Special_Distributions|PDF, CDF and Moments of Special Distributions]]. | ||
| Line 53: | Line 53: | ||
$\sigma_{\rm B} \ = \ $ { 1 3% } $\ \ \rm $ | $\sigma_{\rm B} \ = \ $ { 1 3% } $\ \ \rm $ | ||
| − | {In each case, give the probability that $20 \cdot {\rm lg} \ a ≤ | + | {In each case, give the probability that $20 \cdot {\rm lg} \ a ≤ -10 \ \ \ \rm dB$ ⇒ $a ≤ 0.316$. |
|type="{}"} | |type="{}"} | ||
Channel ${\rm R}\text{:} \hspace{0.4cm} {\rm Pr}(a ≤ 0.316) \ = \ $ { 4.9 3% } $\ \rm \%$ | Channel ${\rm R}\text{:} \hspace{0.4cm} {\rm Pr}(a ≤ 0.316) \ = \ $ { 4.9 3% } $\ \rm \%$ | ||
| Line 63: | Line 63: | ||
+ $v_{\rm B}$ is half as big as $v_{\rm R}$. | + $v_{\rm B}$ is half as big as $v_{\rm R}$. | ||
+ With $v = 0$, $|z(t)|$ would be constant. | + With $v = 0$, $|z(t)|$ would be constant. | ||
| − | - With $v = 0$ $|z(t)|$ would have a white spectrum. | + | - With $v = 0$, $|z(t)|$ would have a white spectrum. |
| − | - With $v → ∞$ $|z(t)|$ would be constant. | + | - With $v → ∞$, $|z(t)|$ would be constant. |
| − | + With $v → ∞$ $|z(t)|$ would be white. | + | + With $v → ∞$, $|z(t)|$ would be white. |
{Which of the following statements are correct? | {Which of the following statements are correct? | ||
|type="[]"} | |type="[]"} | ||
| − | - The | + | - The PDS value ${\it \Phi_z}(f_{\rm D} = 0)$ is the same for both channels. |
+ The ACF value $\varphi_z(\Delta t = 0)$ is the same for both channels. | + The ACF value $\varphi_z(\Delta t = 0)$ is the same for both channels. | ||
+ The area under ${\it \Phi_z}(f_{\rm D})$ is the same for both channels. | + The area under ${\it \Phi_z}(f_{\rm D})$ is the same for both channels. | ||
| Line 76: | Line 76: | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The maximum value of the PDF for both channels is $0.6$ and occurs at $a = 1$. | + | '''(1)''' The maximum value of the PDF for both channels is $0.6$ and occurs at $a = 1$. |
*The Rayleigh PDF and its derivative are | *The Rayleigh PDF and its derivative are | ||
:$$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm},$$ | :$$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm},$$ | ||
| Line 84: | Line 84: | ||
\frac{a^2}{\sigma^4} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm}.$$ | \frac{a^2}{\sigma^4} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm}.$$ | ||
| − | *By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that | + | *By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that |
:$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$ | :$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$ | ||
| Line 95: | Line 95: | ||
| − | '''(3)''' <u>The correct | + | '''(3)''' <u>The correct statements are 2, 3 and 6</u>: |
| − | * The smaller speed $v_{\rm B}$ can be recognized by the fact that the magnitude $|z(t)|$ changes more slowly with the blue curve. | + | * The smaller speed $v_{\rm B}$ can be recognized by the fact that the magnitude $|z(t)|$ changes more slowly with the blue curve. |
| − | * When the vehicle is stationary, the | + | * When the vehicle is stationary, the PDS degenerates to ${\it \Phi_z}(f_{\rm D}) = 2\sigma^2\cdot \delta(f_{\rm D})$, and we have $|z(t)| = A = \rm const.$, where the constant $A$ is drawn from the Rayleigh distribution. |
| − | * At extremely high speed, the Jakes spectrum becomes flat and has an increasingly | + | * At extremely high speed, the Jakes spectrum becomes flat and has an increasingly small magnitude over an increasingly wide range. It then approaches the PDS of white noise. However, $v$ would have to be in the order of the speed of light. |
'''(4)''' <u>Statements 2 and 3</u> are correct: | '''(4)''' <u>Statements 2 and 3</u> are correct: | ||
| − | *The Rayleigh parameter $\sigma = 1$ also determines the | + | *The Rayleigh parameter $\sigma = 1$ also determines the "power" ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process. |
| − | *This applies to both | + | *This applies to both $\rm R$ and $\rm B$: |
:$$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$ | :$$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 109: | Line 109: | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^1.3 Rayleigh Fading with Memory^]] |
Latest revision as of 07:05, 18 September 2022
We consider two different mobile radio channels with Rayleigh fading. In both cases the PDF of the magnitude $a(t) = |z(t)| ≥ 0$ is
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.05cm}.$$
The probability that this magnitude is not greater than a given value $A$ is
- $${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$
The two channels, which are designated according to the colors "Red" and "Blue" in the graphs with $\rm R$ and $\rm B$ respectively, differ in the speed $v$ and thus in the form of the power-spectral density $\rm (PSD)$ ${\it \Phi}_z(f_{\rm D})$.
- In both cases, however, the PDS is a Jakes spectrum.
- For a Doppler frequency $f_{\rm D}$ with $|f_{\rm D}| <f_{\rm D,\hspace{0.1cm}max}$ the Jakes spectrum is given by
- $${\it \Phi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.1cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.1cm} max})^2} } \hspace{0.05cm}.$$
- For Doppler frequencies outside this interval from $-f_{\rm D,\hspace{0.1cm}max}$ to $+f_{\rm D,\hspace{0.1cm}max}$, we have ${\it \Phi}_z(f_{\rm D})=0$.
The corresponding descriptor in the time domain is the auto-correlation function $\rm (ACF)$:
- $$\varphi_z ({\rm \delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.1cm} max} \cdot {\rm \delta}t)\hspace{0.05cm}.$$
- Here, ${\rm J_0}(.)$ is the Bessel function of the first kind and zeroth order. We have ${\rm J_0}(0) = 1$.
- The maximum Doppler frequency of the channel model $\rm R$ is known to be $f_{\rm D,\hspace{0.1cm}max} = 200 \ \rm Hz$.
- It is also known that the speeds $v_{\rm R}$ and $v_{\rm B}$ differ by the factor $2$ .
- Whether $v_{\rm R}$ is twice as large as $v_{\rm B}$ or vice versa, you should decide based on the above graphs.
Notes:
- This task belongs to the topic of Statistical bindings within the Rayleigh process.
- To check your results you can use the interactive applet PDF, CDF and Moments of Special Distributions.
Questionns
Solution
- The Rayleigh PDF and its derivative are
- $$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm},$$
- $$\frac{{\rm d}f_a(a)}{{\rm d}a} \hspace{-0.1cm} = \hspace{-0.1cm} \frac{1}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)}- \frac{a^2}{\sigma^4} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm}.$$
- By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that
- $$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$
(2) As they fading coefficients have the same PDF, the desired probability is also the same for both channels.
- Using the given equation, we have
- $${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm e}^{ -{0.316^2}/(2\sigma^2)} = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} \hspace{0.05cm}.$$
(3) The correct statements are 2, 3 and 6:
- The smaller speed $v_{\rm B}$ can be recognized by the fact that the magnitude $|z(t)|$ changes more slowly with the blue curve.
- When the vehicle is stationary, the PDS degenerates to ${\it \Phi_z}(f_{\rm D}) = 2\sigma^2\cdot \delta(f_{\rm D})$, and we have $|z(t)| = A = \rm const.$, where the constant $A$ is drawn from the Rayleigh distribution.
- At extremely high speed, the Jakes spectrum becomes flat and has an increasingly small magnitude over an increasingly wide range. It then approaches the PDS of white noise. However, $v$ would have to be in the order of the speed of light.
(4) Statements 2 and 3 are correct:
- The Rayleigh parameter $\sigma = 1$ also determines the "power" ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process.
- This applies to both $\rm R$ and $\rm B$:
- $$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$