Difference between revisions of "Aufgaben:Exercise 5.6Z: Gilbert-Elliott Model"

Latest revision as of 03:54, 19 September 2022

Given Gilbert–Elliott model

We consider the burst error channel model according to "E.N. Gilbert" and E.O. Elliott (see sketch). For the transition probabilities let hold:

$${\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)= 0.1, \hspace{0.2cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$

The error probability in the state "GOOD" is $p_{\rm G} = 0.1\%$. For the state "BAD" is $p_{\rm B} = 10\%$.

In the course of this exercise, further parameters are to be determined:

the average error probability $p_{\rm M}$,
the state probabilities $w_{\rm G} = \rm Pr(Z = G)$ and $w_{\rm B} = \rm Pr(Z = B)$,
the values of the correlation function, which for $k > 0$ is given analytically as follows:

$$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot \big [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )\big ]^{\it k} \hspace{0.05cm}.$$

Notes:

The exercise belongs to the chapter "Burst Error Channels".
However, reference is also made to the chapter "Markov chains" in the book "Theory of Stochastic Signals" and in particular to the section "Error correlation function of the Gilbert-Elliott model" in the book "Channel Coding".

Questions

$\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}G) \ = \ $

$\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}B) \hspace{0.2cm} = \ $

$w_{\rm G} \ = \ $

$w_{\rm B} \ = \ $

$p_{\rm M} \ = \ $

$\ \%$

$\varphi_e(k = 1) \hspace{0.35cm} = \ $

$\ \cdot 10^{-4}$

$\varphi_e(k = 2) \hspace{0.35cm} = \ $

$\ \cdot 10^{-4}$

$\varphi_e(k = 5) \hspace{0.35cm} = \ $

$\ \cdot 10^{-4}$

$\varphi_e(k = 50) \ = \ $

$\ \cdot 10^{-4}$

$\varphi_e(k = 0) \ = \ $

$\ \cdot 10^{-2}$

	sole change of $p_{\rm G}$,
	sole change of $p_{\rm B}$,
	sole change of $\rm Pr(G\hspace{0.05cm}\|\hspace{0.05cm}B)$,
	sole change of $\rm Pr(B\hspace{0.05cm}\|\hspace{0.05cm}G)$?

Solution

(1) $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}G) = 1 \, –Pr(B\hspace{0.05cm}|\hspace{0.05cm}G) \ \underline {= 0.99}$ and $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}B) = 1 \, –Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) \ \underline {= 0.9}$ are valid.

(2) The GE model is a stationary Markov chain.

For the probability that it is in the state "GOOD", taking into account the result of subtask (1):

$$w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm B}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm B} \hspace{0.05cm}.$$

Further, $w_{\rm B} = 1 \, –w_{\rm G}$:

$${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)$$

$$\Rightarrow \hspace{0.3cm} w_{\rm G} = \frac{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01} \hspace{0.15cm}\underline {\approx 0.909} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.15cm}\underline {\approx 0.091}\hspace{0.05cm}.$$

(3) The mean error probability $p_{\rm M}$ is obtained from the error probabilities $p_{\rm G}$ and $p_{\rm B}$ weighted by $w_{\rm G}$ and $w_{\rm B}$:

$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \frac{10}{11} \cdot 10^{-3} + \frac{1}{11} \cdot 10^{-1}= \frac{10+100}{11} \cdot 10^{-3}\hspace{0.15cm}\underline { = 1\%}\hspace{0.05cm}.$$

(4) According to the general equation on the specification section, for $k > 0$:

$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm M}^2 + (p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot [1 - {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} = 10^{-4} + 0.09 \cdot 0.009 \cdot 0.89^{\it k} = 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{\it k} \right )\hspace{0.05cm}.$$

$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 1 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 1} \right ) \hspace{0.15cm}\underline {= 8.209 \cdot 10^{-4}} \hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 2 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 2} \right )\hspace{0.15cm}\underline { = 7.416 \cdot 10^{-4}} \hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 5 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 5} \right )\hspace{0.15cm}\underline {= 5.523 \cdot 10^{-4}} \hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 50 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 50} \right ) \hspace{0.15cm}\underline {= 1.024 \cdot 10^{-4}} \hspace{0.05cm}.$$

(5) For each channel model, because of $e_{\nu} ∈ \{0, 1\}$:

$$\varphi_{e}(k = 0 ) = {\rm E}[e_{\nu} ^2] = {\rm E}[e_{\nu} ] = p_{\rm M} \hspace{0.05cm}.$$

Using the result of subtask (3), $\varphi_e(k = 0) \ \underline {= 0.01}$ for the present case.

(6) According to subtask (3) holds:

$$p_{\rm M} = {10}/{11} \cdot p_{\rm G} + {1}/{11} \cdot p_{\rm B} \hspace{0.05cm}.$$

With given $p_{\rm B} = 0.1$, even for $p_{\rm G} = 0$ (no error in state "G"), the average error probability is $p_{\rm M} \approx 0.009$.
In contrast, with fixed $p_{\rm G} = 0.001$ the value $p_{\rm M} = 0.005$ is achievable:

$$0.005 = {10}/{11} \cdot 10^{-3} + {1}/{11} \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} \le 0.055 - 0.1 = 4.5\%\hspace{0.05cm}.$$

Furthermore, the mean error probability (with given $p_{\rm G}$ and $p_{\rm B}$) can also be represented as follows:

$$p_{\rm M} = \frac{p_{\rm G} \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ p_{\rm B} \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.001 \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}\hspace{0.05cm}.$$

With $\rm Pr(B|G) = 0.01$ and with $\rm Pr(G|B) = 0.1$, respectively, the following equations are obtained:

$${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{-0.15cm}:\hspace{0.2cm} {\it p}_{\rm M} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{0.001 \cdot {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.001 }{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + 0.01}\hspace{0.05cm},\hspace{0.5cm} {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) = 0.1\hspace{-0.15cm}:\hspace{0.2cm}{\it p}_{\rm M} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) }\hspace{0.05cm}.$$

From the last equation it can be seen that with no $\rm Pr(G|B)$ value the result $p_{\rm M} = 0.005$ is possible.
On the other hand, with a smaller $\rm Pr(B|G)$ the condition can be fulfilled:

$$0.005 = \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) } \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \le \frac{0.0004}{0.095} \approx 0.0042\hspace{0.05cm}.$$

Solutions 2 and 4 are therefore correct.

@@ Line 1: / Line 1: @@
-{{quiz-Header|Buchseite=Digitalsignalübertragung/Bündelfehlerkanäle}}
+{{quiz-Header|Buchseite=Digital_Signal_Transmission/Burst_Error_Channels}}
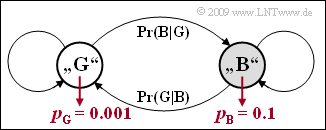
-[[File:P_ID1843__Dig_Z_5_6.png|right|frame|GE–Modell]]
+[[File:P_ID1843__Dig_Z_5_6.png|right|frame|Given Gilbert&ndash;Elliott model]]
-Wir betrachten das <i>Bündelfehler&ndash;Kanalmodell</i> nach E.N. Gilbert und E.O. Elliott (siehe Skizze). Für die Übergangswahrscheinlichkeiten soll dabei gelten:
+We consider the <i>burst error channel model</i>&nbsp; according to &nbsp;[https://en.wikipedia.org/wiki/Edgar_Gilbert "E.N. Gilbert"]&nbsp; and E.O. Elliott (see sketch). For the transition probabilities let hold:
 :$${\rm Pr}(\rm
 G\hspace{0.05cm}|\hspace{0.05cm} B)=  0.1, \hspace{0.2cm} {\rm
 Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
-Die Fehlerwahrscheinlichkeit im Zustand &bdquo;GOOD&rdquo; betrage $p_{\rm G} = 0.1\%$ und für die im Zustand &bdquo;BAD&rdquo; gelte $p_{\rm B} = 10\%$. Im Verlaufe dieser Aufgabe sollen weitere Kenngrößen ermittelt werden:
+The error probability in the state "GOOD" is&nbsp; $p_{\rm G} = 0.1\%$. For the state "BAD" is&nbsp; $p_{\rm B} = 10\%$.
-* die mittlere Fehlerwahrscheinlichkeit $p_{\rm M}$,
-* die Zustandswahrscheinlichkeiten $w_{\rm G} = \rm Pr(Z = G)$ und $w_{\rm B} = \rm Pr(Z = B)$,
+In the course of this exercise, further parameters are to be determined:
-* die Werte der Korrelationsfunktion, die für $k > 0$ analytisch wie folgt gegeben ist:
+* the average error probability&nbsp; $p_{\rm M}$,
+* the state probabilities&nbsp; $w_{\rm G} = \rm Pr(Z = G)$&nbsp; and&nbsp; $w_{\rm B} = \rm Pr(Z = B)$,
+* the values of the correlation function, which for&nbsp; $k > 0$&nbsp; is given analytically as follows:
 :$$\varphi_{e}(k) = p_{\rm M}^2 + (p_{\rm B} -
 p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot
-  [1 - {\rm Pr}(\rm
+  \big [1 - {\rm Pr}(\rm
 B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm
-G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} \hspace{0.05cm}.$$
+G\hspace{0.05cm}|\hspace{0.05cm} B )\big ]^{\it k} \hspace{0.05cm}.$$
-''Hinweis:''
-* Die Aufgabe bezieht sich auf das Kapitel [[Digitalsignal%C3%BCbertragung/B%C3%BCndelfehlerkan%C3%A4le| Bündelfehlerkanal]] des vorliegenden Buches sowie auf das Kapitel [[Stochastische_Signaltheorie/Markovketten| Markovketten]] im Buch &bdquo;Stochastische Signaltheorie&rdquo;.
+''Notes:''
+* The exercise belongs to the chapter&nbsp; [[Digital_Signal_Transmission/Burst_Error_Channels| "Burst Error Channels"]].
+*However, reference is also made to the chapter&nbsp; [[Theory_of_Stochastic_Signals/Markov_Chains| "Markov chains"]]&nbsp; in the book "Theory of Stochastic Signals" and in particular to the section&nbsp; [[Digital_Signal_Transmission/Burst_Error_Channels#Error_correlation_function_of_the_Gilbert-Elliott_model|"Error correlation function of the Gilbert-Elliott model"]]&nbsp; in the book "Channel Coding".
-===Fragebogen===
+===Questions===
 <quiz display=simple>
-{Multiple-Choice
+{What are the following transition probabilities?
-|type="[]"}
+|type="{}"}
-+ correct
+$\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}G) \ = \ ${ 0.99 3% }
-- false
+$\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}B) \hspace{0.2cm} = \ ${ 0.9 3% }
+{With what probabilities is the GE model in the state "GOOD" &nbsp;$(w_{\rm G})$&nbsp; or in the state "BAD" &nbsp;$(w_{\rm B})$?
+|type="{}"}
+$w_{\rm G} \ = \ $ { 0.909 3% }
+$w_{\rm B} \ = \ $ { 0.091 3% }
+{Calculate the mean error probability&nbsp; $p_{\rm M}$.
+|type="{}"}
+$p_{\rm M} \ = \ $ { 1 3% } $\ \%$
+{Calculate the following ECF values:
+|type="{}"}
+$\varphi_e(k = 1) \hspace{0.35cm}  = \ ${ 8.209 3% } $\ \cdot 10^{-4}$
+$\varphi_e(k = 2) \hspace{0.35cm} = \ ${ 7.416 3% } $\ \cdot 10^{-4}$
+$\varphi_e(k = 5) \hspace{0.35cm} = \ ${ 5.523 3% } $\ \cdot 10^{-4}$
+$\varphi_e(k = 50) \ = \ ${ 1.024 3% } $\ \cdot 10^{-4}$
-{Input-Box Frage
+{What is the size of the ECF value&nbsp; $\varphi_e(k = 0)$?
 |type="{}"}
-$xyz \ = \ ${ 5.4 3% } $ab$
+$\varphi_e(k = 0) \ = \ ${ 1 3% } $\ \cdot 10^{-2}$
+{Can the mean error probability&nbsp; $p_{\rm M} = 0.005$&nbsp; be achieved by
+|type="[]"}
+- sole change of&nbsp; $p_{\rm G}$,
++ sole change of&nbsp; $p_{\rm B}$,
+- sole change of&nbsp; $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}B)$,
++ sole change of&nbsp; $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}G)$?
 </quiz>
-===Musterlösung===
+===Solution===
 {{ML-Kopf}}
-'''(1)'''&nbsp;
+'''(1)'''&nbsp; $\rm Pr(G\hspace{0.05cm}|\hspace{0.05cm}G) = 1 \, &ndash;Pr(B\hspace{0.05cm}|\hspace{0.05cm}G) \ \underline {= 0.99}$ and $\rm Pr(B\hspace{0.05cm}|\hspace{0.05cm}B) = 1 \, &ndash;Pr(G\hspace{0.05cm}|\hspace{0.05cm}B) \ \underline {= 0.9}$ are valid.
-'''(2)'''&nbsp;
-'''(3)'''&nbsp;
-'''(4)'''&nbsp;
+'''(2)'''&nbsp; The GE model is a stationary Markov chain.
-'''(5)'''&nbsp;
+*For the probability that it is in the state "GOOD", taking into account the result of subtask '''(1)''':
+:$$w_{\rm G} = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} G) \cdot
+w_{\rm G} + {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot
+w_{\rm B}\hspace{0.3cm}
+\Rightarrow \hspace{0.3cm} {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} = {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm B}
+\hspace{0.05cm}.$$
+*Further, $w_{\rm B} = 1 \, &ndash;w_{\rm G}$:
+:$${\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G) \cdot w_{\rm G} + {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) \cdot w_{\rm G} = {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B)$$
+:$$\Rightarrow \hspace{0.3cm} w_{\rm G} = \frac{{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B)}{{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)} = \frac{0.1}{0.1 + 0.01}
+\hspace{0.15cm}\underline {\approx 0.909} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 -
+w_{\rm G }\hspace{0.15cm}\underline {\approx 0.091}\hspace{0.05cm}.$$
+'''(3)'''&nbsp; The mean error probability $p_{\rm M}$ is obtained from the error probabilities $p_{\rm G}$ and $p_{\rm B}$ weighted by $w_{\rm G}$  and $w_{\rm B}$:
+:$$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B}
+= \frac{10}{11} \cdot 10^{-3} + \frac{1}{11} \cdot 10^{-1}= \frac{10+100}{11} \cdot 10^{-3}\hspace{0.15cm}\underline { =
+\%}\hspace{0.05cm}.$$
+'''(4)'''&nbsp; According to the general equation on the specification section, for $k > 0$:
+:$$\varphi_{e}(k) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} p_{\rm M}^2 +
+(p_{\rm B} - p_{\rm M}) \cdot (p_{\rm M} - p_{\rm G}) \cdot
+ [1 - {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G )- {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B )]^{\it k} = 10^{-4} + 0.09 \cdot 0.009
+\cdot  0.89^{\it k} = 10^{-4} \cdot \left ( 1 + 8.1 \cdot
+.89^{\it k} \right )\hspace{0.05cm}.$$
+:$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 1 ) \hspace{-0.1cm} \ =
+\ \hspace{-0.1cm} 10^{-4} \cdot \left ( 1 + 8.1 \cdot 0.89^{ 1}
+\right ) \hspace{0.15cm}\underline {= 8.209 \cdot 10^{-4}} \hspace{0.05cm},$$
+:$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 2 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4}
+\cdot \left ( 1 + 8.1 \cdot 0.89^{ 2}
+\right )\hspace{0.15cm}\underline { = 7.416 \cdot 10^{-4}} \hspace{0.05cm},$$
+:$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 5 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4}
+\cdot \left ( 1 + 8.1 \cdot 0.89^{ 5}
+\right )\hspace{0.15cm}\underline {= 5.523 \cdot 10^{-4}} \hspace{0.05cm},$$
+:$$\Rightarrow \hspace{0.3cm}\varphi_{e}(k = 50 ) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 10^{-4}
+\cdot \left ( 1 + 8.1 \cdot 0.89^{ 50} \right ) \hspace{0.15cm}\underline {= 1.024 \cdot
+^{-4}} \hspace{0.05cm}.$$
+'''(5)'''&nbsp; For each channel model, because of $e_{\nu} &#8712; \{0, 1\}$:
+:$$\varphi_{e}(k = 0 ) = {\rm E}[e_{\nu} ^2] = {\rm E}[e_{\nu} ] =
+p_{\rm M} \hspace{0.05cm}.$$
+Using the result of subtask '''(3)''', $\varphi_e(k = 0) \ \underline {= 0.01}$ for the present case.
+'''(6)'''&nbsp; According to subtask '''(3)''' holds:
+:$$p_{\rm M} = {10}/{11} \cdot p_{\rm G} + {1}/{11} \cdot
+p_{\rm B} \hspace{0.05cm}.$$
+*With given $p_{\rm B} = 0.1$, even for $p_{\rm G} = 0$ (no error in state "G"), the average error probability is $p_{\rm M} \approx 0.009$.
+*In contrast, with fixed $p_{\rm G} = 0.001$ the value $p_{\rm M} = 0.005$ is achievable:
+:$$0.005 = {10}/{11} \cdot 10^{-3} + {1}/{11} \cdot p_{\rm B}
+\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm B} \le 0.055 - 0.1
+= 4.5\%\hspace{0.05cm}.$$
+*Furthermore, the mean error probability (with given $p_{\rm G}$ and $p_{\rm B}$) can also be represented as follows:
+:$$p_{\rm M} = \frac{p_{\rm G} \cdot {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B)+ p_{\rm B} \cdot {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)} =  \frac{0.001 \cdot {\rm
+Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.1 \cdot {\rm
+Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}{{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) + {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)}\hspace{0.05cm}.$$
+*With $\rm Pr(B|G) = 0.01$ and with $\rm Pr(G|B) = 0.1$, respectively, the following equations are obtained:
+:$${\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) =
+.01\hspace{-0.15cm}:\hspace{0.2cm} {\it p}_{\rm M} \hspace{-0.1cm} \ = \
+\hspace{-0.1cm}  \frac{0.001 \cdot {\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B)+ 0.001 }{{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) +
+.01}\hspace{0.05cm},\hspace{0.5cm}
+{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) =
+.1\hspace{-0.15cm}:\hspace{0.2cm}{\it p}_{\rm M} \hspace{-0.1cm} \ = \
+\hspace{-0.1cm} \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm
+G\hspace{0.05cm}|\hspace{0.05cm} B) }\hspace{0.05cm}.$$
+*From the last equation it can be seen that with no $\rm Pr(G|B)$ value the result $p_{\rm M} = 0.005$ is possible.
+*On the other hand, with a smaller $\rm Pr(B|G)$ the condition can be fulfilled:
+:$$0.005 = \frac{0.0001 + 0.1 \cdot {\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G)}{0.1 +{\rm Pr}(\rm
+B\hspace{0.05cm}|\hspace{0.05cm} G) } \hspace{0.3cm} \Rightarrow
+\hspace{0.3cm}{\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) \le
+\frac{0.0004}{0.095} \approx 0.0042\hspace{0.05cm}.$$
+*<u>Solutions 2 and 4</u> are therefore correct.
 {{ML-Fuß}}
-[[Category:Aufgaben zu Digitalsignalübertragung|^5.3 Bündelfehlerkanäle^]]
+[[Category:Digital Signal Transmission: Exercises|^5.3 Burst Error Channels^]]