Difference between revisions of "Aufgaben:Exercise 1.17: About the Channel Coding Theorem"
From LNTwww
| Line 5: | Line 5: | ||
}} | }} | ||
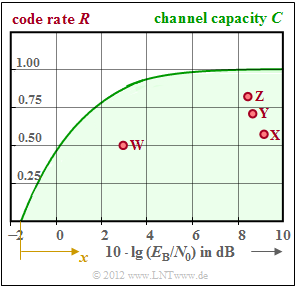
| − | [[File:EN_KC_A_1_17.png|right|frame| | + | [[File:EN_KC_A_1_17.png|right|frame|Channel capacity $($green$)$ and code rates $($red dots$)$ of some established systems]] |
The graph shows the maximum allowable code rate $R < C$ according to Shannon's [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#Channel_coding_theorem_and_channel_capacity|"channel coding theorem"]]: | The graph shows the maximum allowable code rate $R < C$ according to Shannon's [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#Channel_coding_theorem_and_channel_capacity|"channel coding theorem"]]: | ||
| Line 88: | Line 88: | ||
\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$ | \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$ | ||
| − | $10 · \lg {E_{\rm B}/N_0}$ could thus be decreased by $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$, i.e. by a factor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$ | + | * $10 · \lg {E_{\rm B}/N_0}$ could thus be decreased by $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$, i.e. by a factor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 13:38, 28 September 2022
The graph shows the maximum allowable code rate $R < C$ according to Shannon's "channel coding theorem":
- The green limit curve indicates the channel capacity $C$ for the AWGN channel assuming a binary input signal ("BPSK").
- In the "Exercise 1.17Z" a simple approximation is given for this. With the second abscissa
- $$x = \frac {1.6\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}$$
- results approximately:
- $$C \approx \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} \\ \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\ \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$
- If $R < C$ holds, then a code can be found which leads to the error probability "zero" for infinitely long blocks $(n → ∞)$ . What this code looks like is not determined by the channel coding theorem and does not matter for this exercise.
Drawn into the graph as dots are the characteristics of established coding systems:
- The dots $\rm X$, $\rm Y$ and $\rm Z$ mark three Hamming codes of different code lengths, namely with $n = 7$, $n = 15$ and $n = 31$.
- The coding system $\rm W$ is characterized by the parameters $R = 0.5$ and $10 \ - \lg {E_{\rm B}/N_0} = 3 {\rm dB}$ .
Hints:
- This exercise belongs to the topic of chapter "Information Theoretical Limits of Channel Coding".
- The information theoretical limit "channel capacity" refers to the error probability $\rm BER =0$.
- The plotted points of real transmission systems, on the other hand, result under the assumption $\rm BER = 10^{-5}$.
Questions
Solution
(1) Correct are all proposed solutions:
- From the graph you can already see that the rate of $\rm Z$ is greater than the rate of $\rm Y$ and the rate of $\rm Y$ is greater than the rate of $\rm X$.
- The actual rates of these three systems are $R_{\rm X} = 4/7 = 0.571$, $R_{\rm Y} = 11/15 = 0.733$, and $R_{\rm Z} = 26/31 = 0.839$.
- In addition, since the $(31, 26, 3)$ Hamming code ⇒ code $\rm Z$ has the largest codeword length $n$, it requires $n$ despite a larger code rate $R$ for ${\rm BER} = 10^{-5}$ a smaller $E_{\rm B}/N_{0}$ than the other two Hamming codes.
(2) Correct is the answer 2:
- For a smaller bit error rate, one always needs a larger $E_{\rm B}/N_{0}$.
- There is no vertical shift, because even with $\rm BER = 10^{-10}$ there is no change in the code rates.
(3) For the logarithmized AWGN parameter $10 · \lg {E_{\rm B}/N_0} = 3 \ {\rm dB}$, we obtain the auxiliary quantity $x = 1.6 + 3 = 4.6.$ This gives:
- $$R_{\rm max} = C (x = 4.6)= 1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} 4.6} \hspace{0.15cm} \underline{= 0.84} \hspace{0.05cm}.$$
(4) Now, according to the given equation:
- $$1 - {\rm e}^{- 0.4 \hspace{0.05cm} \cdot \hspace{0.05cm} x} = 0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x = \frac{-{\rm ln}(0.5)}{-0.4} = 1.73\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 1.73 - 1.6 = 0.13 \,{\rm dB}\hspace{0.05cm}.$$
- $10 · \lg {E_{\rm B}/N_0}$ could thus be decreased by $3 \ \rm dB - 0.13 \ dB = 2.87 \ dB$, i.e. by a factor $A = 10^{0.287}\hspace{0.15cm} \underline{= 1.94} \hspace{0.05cm}.$