Aufgaben:Exercise 1.12: Hard Decision vs. Soft Decision

• Return to book

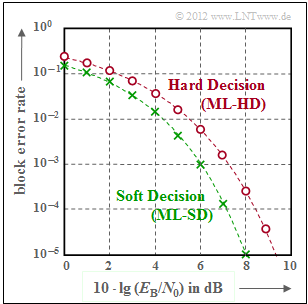
Block error rate of the  $\rm HC(7, \, 4, \, 3)$  for
"Hard Decision" and "Soft Decision" Korrektur

The figure shows the block error probability for the  "$(7, \, 4, \, 3)$ Hamming code",  where two variants are considered for the receiver:

• Maximum likelihood decoding with hard decisions  $($"Hard Decision",  $\rm HD)$,  which in the present case  $($perfect code$)$  can also be realized by syndrome decoding,  yields the red curve  $($with circle marker$)$.

• The channel can be replaced by the BSC model in a simplified way for  "Hard Decision".  The relationship between the BSC parameter  $\varepsilon$  and the AWGN quotient  $E_{\rm B}/N_{0}$  $($used in the graph$)$ is given as follows:

$$\varepsilon = {\rm Q}\left ( \sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \right ) \hspace{0.05cm}.$$

Here  ${\rm Q}(x)$  denotes the  "complementary Gaussian error function"  and  $R$  the code rate.

• The green curve  $($with crosses$)$ shows the block error probability for soft decisions  $($"Soft Decision",  $\rm SD)$.  This curve cannot be given in closed-mathematical form.  The curve drawn in the graph is an upper bound given in  [Fri96]:

$$ {\rm Pr(block\:error)} \hspace{-0.15cm}\ \le \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{ 3 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right )+7 \cdot {\rm Q}\left ( \sqrt{ 4 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) + {\rm Q}\left ( \sqrt{ 7 \cdot \frac{2 \cdot R \cdot E_{\rm B}}{N_0}} \right ) \hspace{0.05cm}.$$

1. The respective first factor in the arguments of the  $\rm Q$–function indicates Hamming distances   ⇒   $i = 3, \, 4, \, 7$.
2. The prefactors take into account  "multiplicities"  $W_{3} = W_{4} = 7$  and  $W_{7} = 1$.  
3. $R = 4/7$  describes the code rate.
4. For  $10 · \lg {E_{\rm B}/N_0} > 8 \ \rm dB$  ⇒   $\rm Pr(block\:error) < 10^{–5}$.

Hints:

• This exercise refers to the chapter  "Decoding of Linear Block Codes".

• The above cited bibliography  [Fri96]  refers to the book
  "Friedrichs, B.: Kanalcodierung - Grundlagen und Anwendungen in modernen Kommunikationssystemen. Berlin - Heidelberg: Springer, 1996".

• For numerical results,  use our calculation applet  "Complementary Gaussian Error Functions".

• For the subtasks  (1)  to  (4),  "Hard Decision" is always assumed.

Questions

1

What is the block error probability of the  $(7, \, 4, \, 3)$ Hamming code in  "Hard Decision"?

$\varepsilon = 10^{-2} \text{:} \hspace{0.4cm} {\rm Pr(block\:error)} \ = \ $ $\ \cdot 10^{-3} $

$\varepsilon = 10^{-3} \text{:} \hspace{0.4cm} {\rm Pr(block\:error)} \ = \ $ $\ \cdot 10^{-3} $

2

How can we approximate the block error probability of a Hamming code,  assuming "Hard Decision"?

	${\rm Pr(block\:error)} = n · (n–1)/2 · \varepsilon^2.$
	${\rm Pr(block\:error)} = n · \varepsilon^2.$
	${\rm Pr(block\:error)} = n · \varepsilon^n.$

3

Which Hamming code has the smallest block error probability with constant BSC parameter  $\varepsilon$?

	the Hamming code  $(3, \, 1, \, 3)$,  identical to the  "repetition code"  $\rm RC \ (3, \, 1, \, 3)$,
	the Hamming code  $(7, \, 4, \, 3)$,
	the Hamming code  $(15, \, 11, \, 3)$.

4

What is the numerical relationship between the BSC parameter  $\varepsilon$  and the AWGN quotient  $E_{\rm B}/N_{0}$?

$\varepsilon = 10^{-2}\text{:} \hspace{0.4cm} 10 · \lg {E_{\rm B}/N_0} \ = \ $ $\ \rm dB$

$\varepsilon = 10^{-3} \text{:} \hspace{0.4cm} 10 · \lg {E_{\rm B}/N_0} \ = \ $ $\ \rm dB$

5

What is the gain  $($in dB$)$  to be achieved by  "Soft Decision"  if the block error probability is not to exceed  $10^{-5}$ ?

$\ 10 · \lg \, {G_{\rm SD}} \ = \ $ $ \ \rm dB$

Solution

Solution

(1)  Every Hamming code is perfect and has the minimum distance  $d_{\rm min} = 3$.

• Therefore,  one bit error in the code word can be corrected,  while two bit errors will always cause the code word to fail   ⇒   parameter  $t = 1$.
• Thus,  for the block error probability:

$${\rm Pr(block\:error)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm Pr(no\hspace{0.15cm} block\:error)} - {\rm Pr(one\hspace{0.15cm} block\:error)} = 1 - (1 - \varepsilon)^7 - 7 \cdot \varepsilon \cdot (1 - \varepsilon)^6 \hspace{0.05cm}.$$

$$\varepsilon = 10^{-2} \text{:} \hspace{0.4cm}{\rm Pr(block\:error)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - 0.99^7 - 7 \cdot 0.01 \cdot 0.99^6= 1 - 0.932065 - 0.065904\hspace{0.15cm}\underline{\approx 2.03 \cdot 10^{-3}}\hspace{0.05cm},$$

$$\varepsilon = 10^{-3} \text{:} \hspace{0.4cm} {\rm Pr(block\:error)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - 0.999^7 - 7 \cdot 0.001 \cdot 0.999^6= 1 - 0.993021 - 0.006958\hspace{0.15cm}\underline{\approx 0.0209 \cdot 10^{-3}}\hspace{0.05cm}.$$

(2)  Each  $(n, \, k, \, 3)$  Hamming code can correct only one bit error.  Thus,  for the BSC channel,  the general rule is with code word length  $n$:

$${\rm Pr(block\:error)} = 1 - \text{Pr(no bit error)} - \text{Pr(one bit error)} = 1 - (1 - \varepsilon)^n - n \cdot \varepsilon \cdot (1 - \varepsilon)^{n-1}.$$

• After series expansion of   "$(1 - \varepsilon)^n$"   or of   "$n \cdot \varepsilon \cdot (1 - \varepsilon)^{n-1}$"   we obtain from this:

$${\rm Pr(block\:error)} = 1 - \left [ 1 - {n \choose 1}\cdot \varepsilon + {n \choose 2}\cdot \varepsilon^2 - \hspace{0.05cm}\text{...} \hspace{0.05cm} \right ] -\left [ n \cdot \varepsilon \cdot \left ( 1 - {{n-1} \choose 1}\cdot \varepsilon + {{n-1} \choose 2}\cdot \varepsilon^2 - \hspace{0.05cm}\text{...} \hspace{0.05cm}\right ) \right ] \hspace{0.05cm}.$$

• If we neglect all terms with  $\varepsilon^3, \ \varepsilon^4, \ \text{...}$  we finally get:

$${\rm Pr(block\:error)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} n \cdot \varepsilon - {n \choose 2}\cdot \varepsilon^2 - n \cdot \varepsilon + n \cdot \varepsilon {{n-1} \choose 1}\cdot \varepsilon + \hspace{0.05cm}\text{...}\hspace{0.05cm} = -n/2 \cdot (n-1)\cdot \varepsilon^2 + n \cdot (n-1)\cdot \varepsilon^2 = n \cdot (n-1)/2 \cdot \varepsilon^2 \hspace{0.05cm}.$$

The correct solution is  suggestion 1.

For the  $(7, \, 4, \, 3)$  Hamming code,  it follows:

$${\rm Pr(block\:error)} \le \left\{ \begin{array}{c} 2.03 \cdot 10^{-3}\\ 2.09 \cdot 10^{-5} \end{array} \right.\quad \begin{array}{*{1}c} {\rm for}\hspace{0.15cm} \varepsilon = 10^{-2} \\ {\rm for}\hspace{0.15cm} \varepsilon = 10^{-3} \\ \end{array} \hspace{0.05cm}.$$

• By comparison with the result of the subtask  (1)  one recognizes the validity of this approximation.  The smaller the BSC falsification probability $\varepsilon$,  the better it is.

(3)  The results of subtask  (2)  can be summarized as follows:

$${\rm Pr(block\:error)} = \left\{ \begin{array}{l} 3 \cdot \varepsilon^2 \\ 21 \cdot \varepsilon^2\\ 105 \cdot \varepsilon^2\\ \end{array} \right.\quad \begin{array}{*{1}l} {\rm for}\hspace{0.15cm} n = 3 \\ {\rm for}\hspace{0.15cm} n = 7 \\ {\rm for}\hspace{0.15cm} n = 15 \\ \end{array} \hspace{0.05cm}.$$

• Right is answer 1.  Of course, the Hamming code with the lowest rate  $R = 1/3$,  i.e. with the greatest relative redundancy,  has the lowest block error probability.

(4)  At Hard Decision,  with the complementary Gaussian error function  ${\rm Q}(x)$:

$$\varepsilon = {\rm Q}\left ( \sqrt{2 \cdot R \cdot E_{\rm B}/N_0} \right )\hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_{\rm B}/N_0 = \frac{[{\rm Q}^{-1}(\varepsilon)]^2}{2R}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}[{\rm Q}^{-1}(\varepsilon)] - 10 \cdot {\rm lg} \hspace{0.1cm} (2R) \hspace{0.05cm}.$$

• From this we obtain with  $\varepsilon = 0.01 \ ⇒ \ {\rm Q}^{–1}(\varepsilon) = 2.33$:

$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}(2.33) - 10 \cdot {\rm lg} \hspace{0.1cm} (8/7) = 7.35\,{\rm dB} - 0.58\,{\rm dB}\hspace{0.15cm}\underline{\approx 6.77\,{\rm dB}}\hspace{0.05cm}.$$

• Analogously,  for  $\varepsilon = 0.001 \ ⇒ \ {\rm Q}^{-1}(\varepsilon) = 3.09$:

$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 20 \cdot {\rm lg} \hspace{0.1cm}(3.09) - 0.58\,{\rm dB}\hspace{0.15cm}\underline{\approx 9.22\,{\rm dB}}\hspace{0.05cm}.$$

(5)  Here we refer to the block error probability  $10^{–5}$.

• According to the result of subtask  (2),  the BSC falsification probability must then not be greater than

$$\varepsilon = \sqrt{{10^{-5}}/{21}} = 6.9 \cdot 10^{-4} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Q}^{-1}(\varepsilon) = 3.2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 9.52\,{\rm dB}\hspace{0.05cm}.$$

• For  "Soft Decision"  according to the specification graph:  $10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = 8\,{\rm dB}\hspace{0.05cm}$   ⇒   $10 · \lg {G_{\rm SD}} \ \underline{= 1.52 \ {\rm dB}}$.