Difference between revisions of "Aufgaben:Exercise 4.14Z: 4-QAM and 4-PSK"
| (26 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation}} |
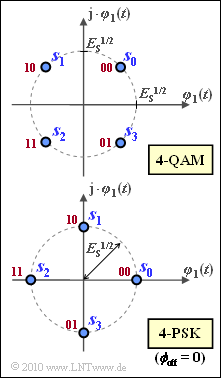
| − | [[File:P_ID2068__Dig_Z_4_14.png|right|frame| | + | [[File:P_ID2068__Dig_Z_4_14.png|right|frame|Signal space constellation of the "4-QAM" and "4-PSK"]] |
| − | + | For [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Quadrature_amplitude_modulation_.28M-QAM.29|"quadrature amplitude modulation"]] $\rm (M–QAM)$, an upper bound ("Union–Bound") on the symbol error probability was given in the theory section for $M ≥ 16$: | |
| − | :$$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \ge p_{\rm S} \hspace{0.05cm}.$$ | + | :$$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$ |
| − | + | In the theory section, one can also find the "Union–Bound" for [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Multi-level_phase.E2.80.93shift_keying_.28M.E2.80.93PSK.29| "M–level phase modulation"]] $\rm (M–PSK)$, | |
| − | :$$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \ge p_{\rm S} \hspace{0.05cm}.$$ | + | :$$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$ |
| − | + | In both methods, each signal space point has exactly the same energy, namely $E_{\rm S}$. | |
| − | + | From the graph, one can see that for the special case $M = 4$, the two modulation processes should actually be identical, which is not directly evident from the above equations. | |
| − | + | The 4–PSK is shown here with the phase offset $\phi_{\rm off} = 0$. With a general phase offset, on the other hand, the in-phase and quadrature components of the signal space points are generally: $(i = 0, \ ... \ , M = 1)$: | |
:$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$ | :$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$ | ||
:$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$ | :$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | Notes: | ||
| + | * The exercise belongs to the chapter [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation| "Carrier Frequency Systems with Coherent Demodulation"]]. | ||
| + | |||
| + | * Reference is made in particular to the sections [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Quadrature_amplitude_modulation_.28M-QAM.29|"Quadrature amplitude modulation"]] and [[Digital_Signal_Transmission/Carrier_Frequency_Systems_with_Coherent_Demodulation#Multi-level_phase.E2.80.93shift_keying_.28M.E2.80.93PSK.29|"Multi-level phase modulation"]]. | ||
| + | |||
| + | * In the above diagram the Gray mapping of the symbols to bit-duples is shown in red. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which phase offset do the 4–QAM and the 4–PSK match exactly? |
|type="{}"} | |type="{}"} | ||
| − | $\phi_{\rm off}$ | + | $\phi_{\rm off}\ = \ $ { 45 3% } $\ \rm degree$ |
| − | { | + | {What is the upper bound $($Union Bound, $p_{\rm UB} ≥ p_{\rm S})$ for the '''4–PSK'''? |
|type="[]"} | |type="[]"} | ||
| − | - $p_{\rm UB} = 4 \cdot {\rm Q}[ | + | - $p_{\rm UB} = 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$, |
| − | + $p_{\rm UB} = 2 \cdot {\rm Q}[ | + | + $p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$, |
| − | - $p_{\rm UB} = 2 \cdot {\rm Q}[ | + | - $p_{\rm UB} = 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$. |
| − | { | + | {Specify a closer upper bound for the '''4–QAM'''. |
|type="[]"} | |type="[]"} | ||
| − | - $p_{\rm S} ≤ 4 \cdot {\rm Q}[ | + | - $p_{\rm S} ≤ 4 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$, |
| − | + $p_{\rm S} ≤ 2 \cdot {\rm Q}[ | + | + $p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{E_{\rm S}/N_0}\hspace{0.05cm}]$, |
| − | - $p_{\rm S} ≤ 2 \cdot {\rm Q}[ | + | - $p_{\rm S} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm S}/N_0}\hspace{0.05cm}]$. |
| − | { | + | {What is the bit error probability bound for the 4–QAM, assuming Gray coding? |
|type="[]"} | |type="[]"} | ||
| − | - $p_{\rm B} ≤ 2 \cdot {\rm Q}[ | + | - $p_{\rm B} ≤ 2 \cdot {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$, |
| − | + $p_{\rm B} ≤ {\rm Q}[ | + | + $p_{\rm B} ≤ {\rm Q}[\sqrt{2E_{\rm B}/N_0}\hspace{0.05cm}]$, |
| − | - $p_{\rm B} ≤ {\rm Q}[ | + | - $p_{\rm B} ≤ {\rm Q}[\sqrt{E_{\rm B}/N_0}\hspace{0.05cm}]$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With $M = 4$, the signal space points are $\boldsymbol{s}_i = (s_{\rm I \it i}, s_{\rm Q \it i})$ of digital phase modulation $(i = 0, \ \text{...} \ , 3)$: |
:$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$ | :$$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$ | ||
:$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$ | :$$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$ | ||
| − | + | *With $\phi_{\rm off} \ \underline {= \pi/2 \ (45^°)}$, we obtain exactly the signal space points of the 4–QAM: | |
| − | :$$\boldsymbol{ s}_{\rm 0} = (+\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 1} = (-\sqrt{2}, +\sqrt{2})\hspace{0.05cm}, | + | :$$\boldsymbol{ s}_{\rm 0} = (+\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 1} = (-\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm 3} = (-\sqrt{2}, -\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 4} = (+\sqrt{2}, -\sqrt{2}) |
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' <u>Solution 2</u> is correct: For the "4–PSK" holds: |
| − | :$$p_{\rm S} \le p_{\rm UB} \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] = | + | :$$p_{\rm S} \le p_{\rm UB} \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] = 2 \cdot {\rm Q} \left [ { 1}/{ \sqrt{2}} \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ]= |
| − | |||
2 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | 2 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | ||
| − | |||
| + | '''(3)''' <u>Solution 2</u> is correct: | ||
| + | *The "4–QAM" is identical with the "4–PSK" (regarding error probability even independent of the phase offset). | ||
| + | |||
| + | *Solution 1, on the other hand, gives the "Union Bound" of the "M–QAM" in general, where $M = 4$ is used. | ||
| + | |||
| + | *However, since there are no inner symbols in "4–QAM", this bound is too pessimistic. | ||
| − | + | *The resulting "Union Bound" is then twice as large as the 4–PSK bound. | |
| − | '''(4)''' | + | |
| + | '''(4)''' Here again the <u>second solution</u> is correct: | ||
| + | *In Gray coding, each symbol error results in a bit error if only adjacent regions are considered: $p_{\rm B} \approx p_{\rm S}/2$. | ||
| + | |||
| + | *Furthermore, $E_{\rm S} = 2 \ E_{\rm B}$ is valid. It follows that | ||
:$$p_{\rm B} = \frac{p_{\rm S}}{2} \le | :$$p_{\rm B} = \frac{p_{\rm S}}{2} \le | ||
{\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | ||
| − | + | *As derived in the solution to [[Aufgaben:Exercise_4.13:_Four-level_QAM|"Exercise 4.13"]], it is even exactly valid''': | |
| − | |||
:$$p_{\rm B} = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | :$$p_{\rm B} = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$ | ||
| + | *In this derivation, it was used that the "4–QAM" can be represented by two orthogonal BPSK modulations (with cosine and minus sinusoidal carriers, respectively). | ||
| + | *Thus, the bit error probability of the "4–QAM" and thus also of the "4–PSK" as a function of $E_{\rm B}/N_0$ is the same as for BPSK. | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 86: | Line 102: | ||
| − | [[Category: | + | [[Category:Digital Signal Transmission: Exercises|^4.4 Coherent Demodulation^]] |
Latest revision as of 16:05, 1 October 2022
For "quadrature amplitude modulation" $\rm (M–QAM)$, an upper bound ("Union–Bound") on the symbol error probability was given in the theory section for $M ≥ 16$:
- $$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$
In the theory section, one can also find the "Union–Bound" for "M–level phase modulation" $\rm (M–PSK)$,
- $$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \hspace{0.05cm}\right ] \ge p_{\rm S} \hspace{0.05cm}.$$
In both methods, each signal space point has exactly the same energy, namely $E_{\rm S}$.
From the graph, one can see that for the special case $M = 4$, the two modulation processes should actually be identical, which is not directly evident from the above equations.
The 4–PSK is shown here with the phase offset $\phi_{\rm off} = 0$. With a general phase offset, on the other hand, the in-phase and quadrature components of the signal space points are generally: $(i = 0, \ ... \ , M = 1)$:
- $$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$
- $$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter "Carrier Frequency Systems with Coherent Demodulation".
- Reference is made in particular to the sections "Quadrature amplitude modulation" and "Multi-level phase modulation".
- In the above diagram the Gray mapping of the symbols to bit-duples is shown in red.
Questions
Solution
- $$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$
- $$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$
- With $\phi_{\rm off} \ \underline {= \pi/2 \ (45^°)}$, we obtain exactly the signal space points of the 4–QAM:
- $$\boldsymbol{ s}_{\rm 0} = (+\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 1} = (-\sqrt{2}, +\sqrt{2})\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{ s}_{\rm 3} = (-\sqrt{2}, -\sqrt{2})\hspace{0.05cm},\hspace{0.2cm}\boldsymbol{ s}_{\rm 4} = (+\sqrt{2}, -\sqrt{2}) \hspace{0.05cm}.$$
(2) Solution 2 is correct: For the "4–PSK" holds:
- $$p_{\rm S} \le p_{\rm UB} \hspace{-0.15cm} \ = \ \hspace{-0.15cm}2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] = 2 \cdot {\rm Q} \left [ { 1}/{ \sqrt{2}} \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ]= 2 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \hspace{0.05cm}.$$
(3) Solution 2 is correct:
- The "4–QAM" is identical with the "4–PSK" (regarding error probability even independent of the phase offset).
- Solution 1, on the other hand, gives the "Union Bound" of the "M–QAM" in general, where $M = 4$ is used.
- However, since there are no inner symbols in "4–QAM", this bound is too pessimistic.
- The resulting "Union Bound" is then twice as large as the 4–PSK bound.
(4) Here again the second solution is correct:
- In Gray coding, each symbol error results in a bit error if only adjacent regions are considered: $p_{\rm B} \approx p_{\rm S}/2$.
- Furthermore, $E_{\rm S} = 2 \ E_{\rm B}$ is valid. It follows that
- $$p_{\rm B} = \frac{p_{\rm S}}{2} \le {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$
- As derived in the solution to "Exercise 4.13", it is even exactly valid:
- $$p_{\rm B} = {\rm Q} \left [ \sqrt{ { 2E_{\rm B}}/{ N_0}} \right ] \hspace{0.05cm}.$$
- In this derivation, it was used that the "4–QAM" can be represented by two orthogonal BPSK modulations (with cosine and minus sinusoidal carriers, respectively).
- Thus, the bit error probability of the "4–QAM" and thus also of the "4–PSK" as a function of $E_{\rm B}/N_0$ is the same as for BPSK.