Difference between revisions of "Theory of Stochastic Signals/Statistical Dependence and Independence"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Wahrscheinlichkeitsrechnung |Vorherige Seite=Mengentheoretische Grundlagen |Nächste Seite=Markovketten }} ==Allgemeine Definition von s…“) |
|||
| Line 34: | Line 34: | ||
*Dagegen bestehen wegen Pr( $A_1$) = 1/2, Pr( $A_4$) = 5/36 und Pr( $A_1 ∩ A_4$) = 1/18 statistische Bindungen zwischen $A_1 = „R < 4”$ und dem im Bild auf der nächsten Seite markierten Ereignis $A_4 = „S = 8”$. Die beiden Ereignisse $A_1 = „R < 4”$ und $A_5 = „S ≥ 10”$ sind sogar disjunkt. Dies zeigt, dass Disjunktivität eine besonders ausgeprägte Form von statistischer Abhängigkeit ist. | *Dagegen bestehen wegen Pr( $A_1$) = 1/2, Pr( $A_4$) = 5/36 und Pr( $A_1 ∩ A_4$) = 1/18 statistische Bindungen zwischen $A_1 = „R < 4”$ und dem im Bild auf der nächsten Seite markierten Ereignis $A_4 = „S = 8”$. Die beiden Ereignisse $A_1 = „R < 4”$ und $A_5 = „S ≥ 10”$ sind sogar disjunkt. Dies zeigt, dass Disjunktivität eine besonders ausgeprägte Form von statistischer Abhängigkeit ist. | ||
{{end}} | {{end}} | ||
| + | |||
| + | ==Bedingte Wahrscheinlichkeit (1)== | ||
| + | Bestehen zwischen den beiden Ereignissen $A$ und $B$ statistische Bindungen, so ist durch die (unbedingten) Wahrscheinlichkeiten Pr( $A$) und Pr( $B$) der Sachverhalt im statistischen Sinne nicht eindeutig beschrieben. Man benötigt dann noch so genannte bedingte Wahrscheinlichkeiten. | ||
| + | |||
| + | {{Definition}} | ||
| + | Die bedingte Wahrscheinlichkeit (englisch: ''Conditional Probability'') von $A$ unter der Bedingung $B$ ist wie folgt berechenbar: | ||
| + | $$\rm Pr(\it A \mid \it B) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it B)}.$$ | ||
| + | {{end}} | ||
| + | |||
| + | |||
| + | In gleicher Weise gilt für die bedingte Wahrscheinlichkeit von $B$ unter der Bedingung $A$: | ||
| + | $$\rm Pr(\it B \mid \it A) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it A)}.$$ | ||
| + | |||
| + | Verknüpft man diese beiden Gleichungen, so ergibt sich der Satz von Bayes: | ||
| + | $$\rm Pr(\it B \mid \it A) = \frac{\rm Pr(\it A \mid \it B)\cdot\rm Pr(\it B)}{\rm Pr(\it A)}.$$ | ||
| + | |||
| + | Nachfolgend sind einige Eigenschaften von bedingten Wahrscheinlichkeiten zusammengestellt: | ||
| + | *Auch eine bedingte Wahrscheinlichkeit liegt stets zwischen 0 und 1 einschließlich dieser beiden Grenzen: 0 ≤ Pr( $A | B$) ≤ 1. | ||
| + | *Kann die Bedingung $B$ als konstant angesehen werden, so gelten alle im Kapitel 1.2 für die unbedingten Wahrscheinlichkeiten Pr( $A$) und Pr( $B$) angegebenen Rechenregeln weiterhin. | ||
| + | *Sind die existierenden Ereignisse $A$ und $B$ disjunkt, so ist Pr( $A | B$) = Pr( $B | A$) = 0. | ||
| + | *Ist $B$ eine echte oder unechte Teilmenge von $A$, so ist Pr( $A | B$) = 1. | ||
| + | *Sind zwei Ereignisse $A$ und $B$ statistisch voneinander unabhängig, so sind deren bedingte Wahrscheinlichkeiten gleich den unbedingten, wie die folgende Rechnung zeigt: | ||
| + | $${\rm Pr}(A \mid B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)} = \frac{{\rm Pr} ( A) \cdot {\rm Pr} ( B)} { {\rm Pr}(B)} = {\rm Pr} ( A).$$ | ||
| + | |||
| + | |||
| + | ==Bedingte Wahrscheinlichkeit (2)== | ||
| + | {{Beispiel}} | ||
| + | Wir betrachten wieder das Zufallsexperiment ''Werfen mit zwei Würfeln'', wobei wie beim letzten Beispiel $S = R + B$ die Summe des roten und des blauen Würfels bezeichnet. Im nachfolgenden Schema ist das Ereignis $A_1 = „R < 4”$ wieder rötlich hinterlegt und das Ereignis $A_4 = „S = 8”$ durch grüne Umrahmungen markiert. | ||
| + | |||
| + | |||
| + | [[File:P_ID505__Sto_T_1_3_S2_neu.png | Beispiel für statistisch abhängige Ereignisse]] | ||
| + | |||
| + | |||
| + | Zu dieser Grafik ist anzumerken: | ||
| + | *Die bedingte Wahrscheinlichkeit Pr( $A_1 | A_4$) = 2/5 (zwei der fünf grün umrandeten Felder sind rot hinterlegt) berechnet sich aus dem Quotienten der Verbundwahrscheinlichkeit Pr( $A_1 ∩ A_4$) = 2/36 und der Wahrscheinlichkeit Pr( $A_4$) = 5/36. | ||
| + | *Da $A_1$ und $A_4$ statistisch abhängig sind, ist Pr( $A_1 | A_4$) = 2/5 ungleich Pr( $A_1$) = 1/2. | ||
| + | *Dieses letzte Ergebnis lässt sich zum Beispiel auch über den Satz von Bayes ableiten: | ||
| + | $${\rm Pr}(A_4 \mid A_1) = \frac{{\rm Pr}(A_1 \mid A_4)\cdot {\rm Pr} ( A_4)} { {\rm Pr}(A_1)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{9} = \frac{2/5 \cdot 5/36}{1/2}.$$ | ||
| + | *Dagegen gelten für $A_1$ und das hierzu statistisch unabhängige Ereignis $A_3 = „S = 7”$ die folgenden bedingten Wahrscheinlichkeiten, siehe Grafik zum letzten Beispiel: | ||
| + | $$\rm Pr(\it A_{\rm 1} \mid \it A_{\rm 3}) = \rm Pr(\it A_{\rm 1}) = \rm 1/2\hspace{0.5cm}bzw.\hspace{0.5cm}\rm Pr(\it A_{\rm 3} \mid \it A_{\rm 1}) = \rm Pr(\it A_{\rm 3}) = \rm 1/6.$$ | ||
| + | {{end}} | ||
| + | |||
| + | ==Allgemeines Multiplikationstheorem== | ||
| + | Wir betrachten weiterhin mehrere Ereignisse $A_i$ mit 1 ≤ $i$ ≤ $I$. Diese Ereignisse $A_i$ stellen nun aber kein vollständiges System mehr dar, das heißt, sie sind nicht paarweise zueinander disjunkt, und es können zwischen den einzelnen Ereignissen auch statistische Bindungen bestehen. | ||
| + | |||
| + | {{Definition}} | ||
| + | Für die so genannte Verbundwahrscheinlichkeit, also für die Wahrscheinlichkeit der Schnittmenge aller $I$ Ereignisse $A_i$, gilt in diesem Fall: | ||
| + | $$\rm Pr(\it A_{\rm 1} \cap \hspace{0.1cm} ...\hspace{0.1cm} \cap A_{I}) = \hspace{0.3cm} ...$$ | ||
| + | $$...\hspace{0.3cm}= \rm Pr(\it A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}\rm Pr(\it A_{I \rm \hspace{-0.05cm}-\hspace{-0.05cm}1} \hspace{0.05cm}| \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}\rm Pr(\it A_{I \rm \hspace{-0.05cm} -\hspace{-0.05cm}2} \hspace{0.05cm}| \hspace{0.05cm} \it A_{I \hspace{-0.05cm} - \hspace{-0.05cm} \rm 1}\cap \it A_I)\hspace{0.05cm} \cdot ... \cdot\hspace{0.05cm} \rm Pr(\it A_{\rm 1} \hspace{0.05cm}| \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.1cm} ... \hspace{0.1cm}\cap A_{ I}).$$ | ||
| + | {{end}} | ||
| + | |||
| + | |||
| + | In gleicher Weise gilt natürlich auch: | ||
| + | $$\rm Pr(\it A_{\rm 1} \cap \hspace{0.1cm} ...\hspace{0.1cm} \cap A_{I}) = \hspace{0.3cm} ...$$ | ||
| + | $$...\hspace{0.3cm}= {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}| \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}| \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot ... \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}| \hspace{0.05cm}A_1 \cap \hspace{0.1cm} ... \hspace{0.1cm}\cap A_{ I-1}).$$ | ||
| + | |||
| + | {{Beispiel}} | ||
| + | Eine Lostrommel enthält zehn Lose, darunter drei Treffer (Ereignis $T$). Dann ergibt sich für die Wahrscheinlichkeit, dass man mit zwei Losen zwei Treffer zieht: | ||
| + | $$\rm Pr(\it T_{\rm 1} \cap \it T_{\rm 2}) = \rm Pr(\it T_{\rm1})\cdot \rm Pr(\it T_{\rm 2} \hspace{0.05cm}| \hspace{0.05cm} \it T_{\rm 1}) = \rm 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$ | ||
| + | |||
| + | Hierbei ist berücksichtigt, dass sich bei der zweiten Ziehung nur mehr neun Lose und zwei Treffer in der Urne befinden. | ||
| + | |||
| + | Würde man jedoch die Lose nach der Ziehung wieder in die Trommel zurücklegen, so wären die Ereignisse $T_1$ und $T_2$ statistisch unabhängig ⇒ $ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9%.$ | ||
| + | {{end}} | ||
| + | |||
| + | |||
Revision as of 20:25, 19 May 2016
Contents
Allgemeine Definition von statistischer Abhängigkeit (1)
Bisher haben wir die statistische Abhängigkeit zwischen Ereignissen nicht besonders beachtet, auch wenn wir sie wie im Fall zweier disjunkter Mengen bereits verwendet haben: Gehört ein Element zu $A$, so kann es mit Sicherheit nicht auch in der disjunkten Menge $B$ enthalten sein.
Die stärkste Form von Abhängigkeit überhaupt ist eine deterministische Abhängigkeit zwischen zwei Mengen bzw. zwei Ereignissen. Weniger ausgeprägt ist die statistische Abhängigkeit. Beginnen wir mit deren Komplement:
Zwei Ereignisse $A$ und $B$ bezeichnet man dann als statistisch unabhängig (englisch: statistical independent) , wenn die Wahrscheinlichkeit der Schnittmenge $A ∩ B$ gleich dem Produkt der Einzelwahrscheinlichkeiten ist: $$\rm Pr(\it A \cap \it B) = \rm Pr(\it A)\cdot \rm Pr(\it B).$$
In manchen Anwendungsfällen ist die statistische Unabhängigkeit offensichtlich, zum Beispiel beim Experiment Münzwurf. Die Wahrscheinlichkeit für Zahl oder Bild ist unabhängig davon, ob beim letzten Wurf Zahl oder Bild aufgetreten ist. Und auch die einzelnen Ergebnisse beim Zufallsexperiment Werfen einer Roulettekugel sind bei fairen Bedingungen stets statistisch unabhängig voneinander, auch wenn einzelne Systemspieler dies nicht wahrhaben wollen.
Bei anderen Anwendungen ist dagegen die Frage, ob zwei Ereignisse statistisch unabhängig sind oder nicht, gefühlsmäßig nicht oder nur sehr schwer zu beantworten. Hier kann man nur durch Überprüfung des oben angegebenen formalen Unabhängigkeitskriteriums zur richtigen Antwort gelangen, wie das Beispiel auf der nächsten Seite zeigen soll.
Allgemeine Definition von statistischer Abhängigkeit (2)
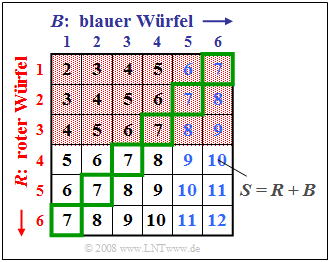
Wir betrachten wieder das Zufallsexperiment Werfen mit zwei Würfeln, wobei die beiden Würfel an ihren Farben Rot $(R)$ und Blau $(B)$ unterschieden werden können. Die Grafik soll diesen Sachverhalt verdeutlichen, wobei in dem zweidimensionalen Feld $(R, B)$ die Summe $S = R + B$ eingetragen ist.
Die Grafik kann wie folgt interpretiert werden:
- Die beiden Ereignisse $A_1 = „R < 4”$ und $A_2 = „B > 4”$ sind im Bild durch rötlichen Hintergrund bzw. blaue Zahlen hervorgehoben. $A_1$ und $A_2$ sind statistisch unabhängig, da die Wahrscheinlichkeit der Schnittmenge – also Pr( $A_1 ∩ A_2$) = 1/6 – gleich dem Produkt der beiden Einzelwahrscheinlichkeiten Pr( $A_1$) = 1/2 und Pr( $A_2$) = 1/3 ist. Aufgrund der Aufgabenstellung hätte auch jedes andere Ergebnis sehr überrascht.
- Aber auch die beiden Ereignisse $A_1 = „R < 4”$ und $A_3 = „S = 7”$ sind wegen Pr( $A_1$) = 1/2, Pr( $A_3$) = 1/6 und Pr( $A_1 ∩ A_3$) = 1/12 statistisch voneinander unabhängig. Das Ereignis $„S =$ 7” ist in der Grafik durch grüne Umrahmungen gekennzeichnet.
- Dagegen bestehen wegen Pr( $A_1$) = 1/2, Pr( $A_4$) = 5/36 und Pr( $A_1 ∩ A_4$) = 1/18 statistische Bindungen zwischen $A_1 = „R < 4”$ und dem im Bild auf der nächsten Seite markierten Ereignis $A_4 = „S = 8”$. Die beiden Ereignisse $A_1 = „R < 4”$ und $A_5 = „S ≥ 10”$ sind sogar disjunkt. Dies zeigt, dass Disjunktivität eine besonders ausgeprägte Form von statistischer Abhängigkeit ist.
Bedingte Wahrscheinlichkeit (1)
Bestehen zwischen den beiden Ereignissen $A$ und $B$ statistische Bindungen, so ist durch die (unbedingten) Wahrscheinlichkeiten Pr( $A$) und Pr( $B$) der Sachverhalt im statistischen Sinne nicht eindeutig beschrieben. Man benötigt dann noch so genannte bedingte Wahrscheinlichkeiten.
Die bedingte Wahrscheinlichkeit (englisch: Conditional Probability) von $A$ unter der Bedingung $B$ ist wie folgt berechenbar: $$\rm Pr(\it A \mid \it B) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it B)}.$$
In gleicher Weise gilt für die bedingte Wahrscheinlichkeit von $B$ unter der Bedingung $A$:
$$\rm Pr(\it B \mid \it A) = \frac{\rm Pr(\it A \cap \it B)}{\rm Pr(\it A)}.$$
Verknüpft man diese beiden Gleichungen, so ergibt sich der Satz von Bayes: $$\rm Pr(\it B \mid \it A) = \frac{\rm Pr(\it A \mid \it B)\cdot\rm Pr(\it B)}{\rm Pr(\it A)}.$$
Nachfolgend sind einige Eigenschaften von bedingten Wahrscheinlichkeiten zusammengestellt:
- Auch eine bedingte Wahrscheinlichkeit liegt stets zwischen 0 und 1 einschließlich dieser beiden Grenzen: 0 ≤ Pr( $A | B$) ≤ 1.
- Kann die Bedingung $B$ als konstant angesehen werden, so gelten alle im Kapitel 1.2 für die unbedingten Wahrscheinlichkeiten Pr( $A$) und Pr( $B$) angegebenen Rechenregeln weiterhin.
- Sind die existierenden Ereignisse $A$ und $B$ disjunkt, so ist Pr( $A | B$) = Pr( $B | A$) = 0.
- Ist $B$ eine echte oder unechte Teilmenge von $A$, so ist Pr( $A | B$) = 1.
- Sind zwei Ereignisse $A$ und $B$ statistisch voneinander unabhängig, so sind deren bedingte Wahrscheinlichkeiten gleich den unbedingten, wie die folgende Rechnung zeigt:
$${\rm Pr}(A \mid B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)} = \frac{{\rm Pr} ( A) \cdot {\rm Pr} ( B)} { {\rm Pr}(B)} = {\rm Pr} ( A).$$
Bedingte Wahrscheinlichkeit (2)
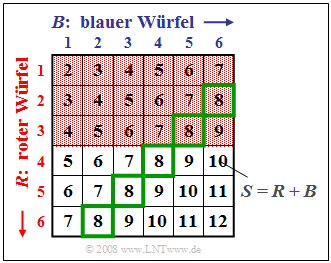
Wir betrachten wieder das Zufallsexperiment Werfen mit zwei Würfeln, wobei wie beim letzten Beispiel $S = R + B$ die Summe des roten und des blauen Würfels bezeichnet. Im nachfolgenden Schema ist das Ereignis $A_1 = „R < 4”$ wieder rötlich hinterlegt und das Ereignis $A_4 = „S = 8”$ durch grüne Umrahmungen markiert.
Zu dieser Grafik ist anzumerken:
- Die bedingte Wahrscheinlichkeit Pr( $A_1 | A_4$) = 2/5 (zwei der fünf grün umrandeten Felder sind rot hinterlegt) berechnet sich aus dem Quotienten der Verbundwahrscheinlichkeit Pr( $A_1 ∩ A_4$) = 2/36 und der Wahrscheinlichkeit Pr( $A_4$) = 5/36.
- Da $A_1$ und $A_4$ statistisch abhängig sind, ist Pr( $A_1 | A_4$) = 2/5 ungleich Pr( $A_1$) = 1/2.
- Dieses letzte Ergebnis lässt sich zum Beispiel auch über den Satz von Bayes ableiten:
$${\rm Pr}(A_4 \mid A_1) = \frac{{\rm Pr}(A_1 \mid A_4)\cdot {\rm Pr} ( A_4)} { {\rm Pr}(A_1)} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{9} = \frac{2/5 \cdot 5/36}{1/2}.$$
- Dagegen gelten für $A_1$ und das hierzu statistisch unabhängige Ereignis $A_3 = „S = 7”$ die folgenden bedingten Wahrscheinlichkeiten, siehe Grafik zum letzten Beispiel:
$$\rm Pr(\it A_{\rm 1} \mid \it A_{\rm 3}) = \rm Pr(\it A_{\rm 1}) = \rm 1/2\hspace{0.5cm}bzw.\hspace{0.5cm}\rm Pr(\it A_{\rm 3} \mid \it A_{\rm 1}) = \rm Pr(\it A_{\rm 3}) = \rm 1/6.$$
Allgemeines Multiplikationstheorem
Wir betrachten weiterhin mehrere Ereignisse $A_i$ mit 1 ≤ $i$ ≤ $I$. Diese Ereignisse $A_i$ stellen nun aber kein vollständiges System mehr dar, das heißt, sie sind nicht paarweise zueinander disjunkt, und es können zwischen den einzelnen Ereignissen auch statistische Bindungen bestehen.
Für die so genannte Verbundwahrscheinlichkeit, also für die Wahrscheinlichkeit der Schnittmenge aller $I$ Ereignisse $A_i$, gilt in diesem Fall: $$\rm Pr(\it A_{\rm 1} \cap \hspace{0.1cm} ...\hspace{0.1cm} \cap A_{I}) = \hspace{0.3cm} ...$$ $$...\hspace{0.3cm}= \rm Pr(\it A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}\rm Pr(\it A_{I \rm \hspace{-0.05cm}-\hspace{-0.05cm}1} \hspace{0.05cm}| \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}\rm Pr(\it A_{I \rm \hspace{-0.05cm} -\hspace{-0.05cm}2} \hspace{0.05cm}| \hspace{0.05cm} \it A_{I \hspace{-0.05cm} - \hspace{-0.05cm} \rm 1}\cap \it A_I)\hspace{0.05cm} \cdot ... \cdot\hspace{0.05cm} \rm Pr(\it A_{\rm 1} \hspace{0.05cm}| \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.1cm} ... \hspace{0.1cm}\cap A_{ I}).$$
In gleicher Weise gilt natürlich auch:
$$\rm Pr(\it A_{\rm 1} \cap \hspace{0.1cm} ...\hspace{0.1cm} \cap A_{I}) = \hspace{0.3cm} ...$$
$$...\hspace{0.3cm}= {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}| \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}| \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot ... \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}| \hspace{0.05cm}A_1 \cap \hspace{0.1cm} ... \hspace{0.1cm}\cap A_{ I-1}).$$
Eine Lostrommel enthält zehn Lose, darunter drei Treffer (Ereignis $T$). Dann ergibt sich für die Wahrscheinlichkeit, dass man mit zwei Losen zwei Treffer zieht: $$\rm Pr(\it T_{\rm 1} \cap \it T_{\rm 2}) = \rm Pr(\it T_{\rm1})\cdot \rm Pr(\it T_{\rm 2} \hspace{0.05cm}| \hspace{0.05cm} \it T_{\rm 1}) = \rm 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$
Hierbei ist berücksichtigt, dass sich bei der zweiten Ziehung nur mehr neun Lose und zwei Treffer in der Urne befinden.
Würde man jedoch die Lose nach der Ziehung wieder in die Trommel zurücklegen, so wären die Ereignisse $T_1$ und $T_2$ statistisch unabhängig ⇒ $ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9%.$