Difference between revisions of "Aufgaben:Exercise 2.11Z: Erasure Channel for Symbols"
| (29 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel}} |
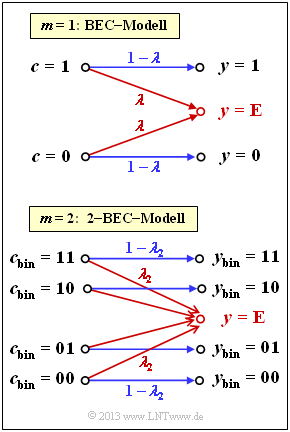
| − | [[File:|right|]] | + | [[File:P_ID2543__KC_Z_2_11.png|right|frame|Erasure channel for symbols: "m–BEC"]] |
| + | The channel model [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|"Binary Erasure Channel"]] $\rm (BEC)$ describes a bit-level erasure channel: | ||
| + | *A binary symbol $(0$ or $1)$ is correctly transmitted with probability $1 - \lambda$ and marked as an erasure "$\rm E$" with probability $\lambda$. | ||
| + | |||
| + | *In contrast to the [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC| "Binary Symmetric Channel"]] $\rm (BSC)$, falsifications $(0 → 1, \ 1 → 0)$ cannot occur here. | ||
| + | A Reed–Solomon code is based on a Galois field ${\rm GF}(2^m)$ with integer $m$. Thus, each code symbol $c$ can be represented by $m$ bits. If one wants to apply the BEC model here, one has to modify it to the "$m$–BEC" model as shown in the diagram below for $m = 2$: | ||
| − | === | + | *All code symbols $($in binary representation $00, \ 01, \ 10, \ 11)$ are transmitted correctly with probability $1 - \lambda_2$ . |
| + | |||
| + | *Thus, the probability of an erased symbol is $\lambda_2$. | ||
| + | |||
| + | *Note that already a single erased bit leads to the erased received symbol $y = \rm E$ . | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | * This exercise belongs to the chapter [[Channel_Coding/Reed-Solomon_Decoding_for_the_Erasure_Channel| "Reed–Solomon Decoding for the Erasure Channel"]]. | ||
| + | |||
| + | * For a code based on ${\rm GF}(2^m)$ the outlined $2$–BEC model is to be extended to $m$–BEC. | ||
| + | |||
| + | *The erasure probability of this model is then denoted by $\lambda_m$. | ||
| + | |||
| + | *For the first subtasks, use always $\lambda = 0.2$ for the erasure probability of the basic model according to the upper graph. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {$\lambda = 0.2$ is valid. With what probabilities do the possible received values occur in the BEC basic model ? |
| − | |type=" | + | |type="{}"} |
| − | + | ${\rm Pr}(y = 0) \ = \ ${ 40 3% } $\ \%$ | |
| − | + | ${\rm Pr}(y = {\rm E}) \ = \ ${ 20 3% } $\ \%$ | |
| + | ${\rm Pr}(y = {\rm 1}) \ = \ ${ 40 3% } $\ \%$ | ||
| + | |||
| + | {$\lambda = 0.2$ is valid. What is the erasure probability $\lambda_2$ at symbol level $(2$–BEC model$)$ when the Reed-Solomon code is based on $\rm GF(2^2)$? | ||
| + | |type="{}"} | ||
| + | $\lambda_2 \ = \ ${ 36 3% } $\ \%$ | ||
| + | |||
| + | {$\lambda = 0.2$ is valid. What is the erasure probability $\lambda_m$, when the $m$–BEC model is fitted to the $\rm RSC \, (255, \, 223, \, 33)_{256}$? | ||
| + | |type="{}"} | ||
| + | $\lambda_m \ = \ ${ 83.2 3% } $\ \%$ | ||
| + | |||
| + | {What is the maximum allowed erasure probability $\lambda$ of the "BEC basic model" for $\lambda_m ≤ 0.2$ to hold? | ||
| + | |type="{}"} | ||
| + | ${\rm Max} \ \big[\lambda\big ] \ = \ ${ 2.75 3% } $\ \%$ | ||
| − | { | + | {What is the probability of receiving the "zero symbol" in this case? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\rm Pr}(y_{\rm bin} = 00000000) \ = \ ${ 0.3125 3% } $\ \%$ |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Due to the symmetry of the given BEC model ("bit-level erasure channel"), the erasure probability is: |
| − | '''(2)''' | + | :$$\ {\rm Pr}(y = {\rm E}) = \lambda \ \underline{= 20\%}.$$ |
| − | '''(3)''' | + | *Since the code symbols $0$ and $1$ are equally likely, we obtain ${\rm Pr}(y = 0) \ \underline{= 40\%}$ and ${\rm Pr}(y = 1) \ \underline{= 40\%}$ for their probabilities. |
| − | '''(4)''' | + | |
| − | '''(5)''' | + | |
| + | |||
| + | '''(2)''' Without limiting generality, we assume the code symbol $c_{\rm bin} = $ "$00$" to solve this exercise. | ||
| + | *According to the $2$–BEC model, the received symbol $y_{\rm bin}$ can then be either "$00$" or erased $(\rm E)$ and it holds: | ||
| + | :$${\rm Pr}(y_{\rm bin} = "00"\hspace{0.05cm} |\hspace{0.05cm} c_{\rm bin} = "00") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} ( 1 - \lambda)^2 = 0.8^2 = 0.64 = 1 - \lambda_2\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} \lambda_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - ( 1 - \lambda)^2 \hspace{0.15cm}\underline{= 36\%}\hspace{0.05cm}. $$ | ||
| + | *This assumes that an erasure is avoided only if neither of the two bits has been erased. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The $\rm RSC \, (255, \, 223, \, 33)_{256}$ is based on the Galois field $\rm GF(256) = GF(2^8) \ \Rightarrow \ \it m = \rm 8$. | ||
| + | *The result of subtask '''(2)''' must now be adapted to this case. For the $8$–BEC holds: | ||
| + | :$$1 - \lambda_8 = ( 1 - \lambda)^8 = 0.8^8 \approx 0.168 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| + | \lambda_m = \lambda_8 \hspace{0.15cm}\underline{\approx 83.2\%}\hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' From the condition $\lambda_m ≤ 0.2$ it follows directly $1 - \lambda_m ≥ 0.8$. From this follows further: | ||
| + | :$$( 1 - \lambda)^8 \ge 0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| + | 1 - \lambda \ge 0.8^{0.125} \approx 0.9725 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda \hspace{0.15cm} | ||
| + | \underline{\le 2.75\%}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Here one proceeds as follows: | ||
| + | *With $\lambda = 0.0275 \Rightarrow \ \lambda_m = 0.2$ ⇒ $20\%$ of the received symbols are erasured. | ||
| + | |||
| + | *The $2^8 = 256$ received symbols $(00000000$ ... $11111111)$ are all equally likely. It follows: | ||
| + | :$${\rm Pr}(y_{\rm bin} = 00000000) = \hspace{0.1cm}\text{...} \hspace{0.1cm}= {\rm Pr}(y_{\rm bin} = 11111111)= \frac{0.8}{256} \hspace{0.15cm}\underline{= 0.3125\%}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Channel Coding: Exercises|^2.4 Reed-Solomon Decoding at the BEC^]] |
Latest revision as of 14:12, 21 October 2022
The channel model "Binary Erasure Channel" $\rm (BEC)$ describes a bit-level erasure channel:
- A binary symbol $(0$ or $1)$ is correctly transmitted with probability $1 - \lambda$ and marked as an erasure "$\rm E$" with probability $\lambda$.
- In contrast to the "Binary Symmetric Channel" $\rm (BSC)$, falsifications $(0 → 1, \ 1 → 0)$ cannot occur here.
A Reed–Solomon code is based on a Galois field ${\rm GF}(2^m)$ with integer $m$. Thus, each code symbol $c$ can be represented by $m$ bits. If one wants to apply the BEC model here, one has to modify it to the "$m$–BEC" model as shown in the diagram below for $m = 2$:
- All code symbols $($in binary representation $00, \ 01, \ 10, \ 11)$ are transmitted correctly with probability $1 - \lambda_2$ .
- Thus, the probability of an erased symbol is $\lambda_2$.
- Note that already a single erased bit leads to the erased received symbol $y = \rm E$ .
Hints:
- This exercise belongs to the chapter "Reed–Solomon Decoding for the Erasure Channel".
- For a code based on ${\rm GF}(2^m)$ the outlined $2$–BEC model is to be extended to $m$–BEC.
- The erasure probability of this model is then denoted by $\lambda_m$.
- For the first subtasks, use always $\lambda = 0.2$ for the erasure probability of the basic model according to the upper graph.
Questions
Solution
- $$\ {\rm Pr}(y = {\rm E}) = \lambda \ \underline{= 20\%}.$$
- Since the code symbols $0$ and $1$ are equally likely, we obtain ${\rm Pr}(y = 0) \ \underline{= 40\%}$ and ${\rm Pr}(y = 1) \ \underline{= 40\%}$ for their probabilities.
(2) Without limiting generality, we assume the code symbol $c_{\rm bin} = $ "$00$" to solve this exercise.
- According to the $2$–BEC model, the received symbol $y_{\rm bin}$ can then be either "$00$" or erased $(\rm E)$ and it holds:
- $${\rm Pr}(y_{\rm bin} = "00"\hspace{0.05cm} |\hspace{0.05cm} c_{\rm bin} = "00") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} ( 1 - \lambda)^2 = 0.8^2 = 0.64 = 1 - \lambda_2\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_2 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - ( 1 - \lambda)^2 \hspace{0.15cm}\underline{= 36\%}\hspace{0.05cm}. $$
- This assumes that an erasure is avoided only if neither of the two bits has been erased.
(3) The $\rm RSC \, (255, \, 223, \, 33)_{256}$ is based on the Galois field $\rm GF(256) = GF(2^8) \ \Rightarrow \ \it m = \rm 8$.
- The result of subtask (2) must now be adapted to this case. For the $8$–BEC holds:
- $$1 - \lambda_8 = ( 1 - \lambda)^8 = 0.8^8 \approx 0.168 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_m = \lambda_8 \hspace{0.15cm}\underline{\approx 83.2\%}\hspace{0.05cm}. $$
(4) From the condition $\lambda_m ≤ 0.2$ it follows directly $1 - \lambda_m ≥ 0.8$. From this follows further:
- $$( 1 - \lambda)^8 \ge 0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1 - \lambda \ge 0.8^{0.125} \approx 0.9725 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\lambda \hspace{0.15cm} \underline{\le 2.75\%}\hspace{0.05cm}.$$
(5) Here one proceeds as follows:
- With $\lambda = 0.0275 \Rightarrow \ \lambda_m = 0.2$ ⇒ $20\%$ of the received symbols are erasured.
- The $2^8 = 256$ received symbols $(00000000$ ... $11111111)$ are all equally likely. It follows:
- $${\rm Pr}(y_{\rm bin} = 00000000) = \hspace{0.1cm}\text{...} \hspace{0.1cm}= {\rm Pr}(y_{\rm bin} = 11111111)= \frac{0.8}{256} \hspace{0.15cm}\underline{= 0.3125\%}\hspace{0.05cm}.$$