Difference between revisions of "Aufgaben:Exercise 1.3: Frame Structure of ISDN"
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/ISDN_Basic_Access |
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_A_1_3.png|right|frame|Frame structure of the $\rm S_{0}$ interface]] |
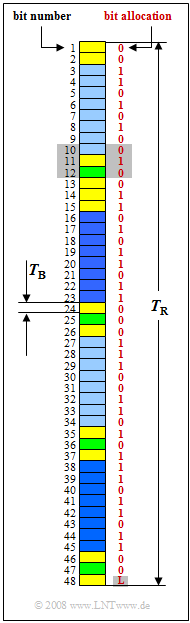
| − | + | The graphic shows the frame structure of the $\rm S_{0}$ interface. Each frame of duration $T_{\rm R}$ contains $48$ bits, among them: | |
| − | *$16$ | + | *$16$ bits for the bearer channel $\rm B1$ $($light blue$)$, |
| − | |||
| − | |||
| + | *$16$ bits for the bearer channel $\rm B2$ $($dark blue$)$, | ||
| − | + | *$4$ bits for the data channel $\rm D$ $($green$)$. | |
| − | |||
| − | + | The required control bits are shown in yellow. | |
| + | For this exercise, it is specified that each of the two base channels $\rm B1$ and $\rm B2$ should provide a net data rate of $R_{\rm B} = 64 \ \rm kbit/s$. | ||
| − | + | It should also be noted that the bit duration $T_{\rm B}$ of the uncoded binary signal simultaneously indicates the symbol duration of the $($modified$)$ AMI code, | |
| − | * | + | *which assigns each binary "$1$" to the voltage level $0 \ \rm V$ and |
| − | |||
| + | *alternately represents each binary "$0$" with $+0.75 \ \rm V$ resp. $–0.75 \ \rm V$. | ||
| + | The numerical values in the graphic $($marked in red$)$ indicate an example sequence which is to be converted into voltage levels in subtask '''(5)''' according to the modified AMI code. | ||
| + | *Bit number $48$ contains the so-called "$\rm L$ bit. | ||
| + | *This is to be set in subtask '''(6)''' in such a way that the signal $s(t)$ becomes DC–free. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | <u>Notes:</u> | ||
| + | *This exercise is part of the chapter [[Examples_of_Communication_Systems/ISDN_Basic_Access|"ISDN Basic Access"]]. | ||
| + | |||
| + | *The AMI code is described in detail in the chapter [[Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes#Properties_of_the_AMI_code|"Properties of the AMI code"]] of the book "Digital Signal Transmission". | ||
| + | *It should also be noted that the first $47$ bits contain exactly $22$ "zeros". | ||
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the frame duration $($German: "Rahmendauer" ⇒ subscript "R"$)$ $T_{\rm R}$? |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm R} \ = \ $ { 250 3% } $\ \rm | + | $T_{\rm R} \ = \ $ { 250 3% } $\ \rm µ s$ |
| − | { | + | {What is the bit duration $T_{\rm B}$? Note: This is equal to the symbol duration after AMI coding. |
|type="{}"} | |type="{}"} | ||
| − | $T_{\rm B} \ = \ $ { 5.208 3% } $\ \rm | + | $T_{\rm B} \ = \ $ { 5.208 3% } $\ \rm µ s $ |
| − | { | + | {What is the total gross data rate $R_{\rm gross}$? |
|type="{}"} | |type="{}"} | ||
| − | $R_{\rm | + | $R_{\rm gross} \ = \ $ { 192 3% } $\ \rm kbit/s$ |
| − | { | + | {How many control bits $(N_{\rm CB})$ are transmitted per frame? |
|type="{}"} | |type="{}"} | ||
| − | $N_{\rm | + | $N_{\rm CB} \ = \ $ { 12 3% } |
| − | { | + | {With which voltage values $(0 \ {\rm V}, +0.75 \ {\rm V}, \ –0.75 \ {\rm V})$ are the bits 10, 11 and 12 (gray shaded block) represented? |
|type="{}"} | |type="{}"} | ||
$U_{10} \ = \ $ { -0.8025--0.6975 } $\ \rm V $ | $U_{10} \ = \ $ { -0.8025--0.6975 } $\ \rm V $ | ||
| Line 60: | Line 67: | ||
$U_{12} \ = \ $ { 0.75 3% } $\ \rm V $ | $U_{12} \ = \ $ { 0.75 3% } $\ \rm V $ | ||
| − | { | + | {What is the voltage value $(0 \ {\rm V}, +0.75 \ {\rm V}, \ –0.75 \ {\rm V})$ of the $\rm L$ bit at the end? |
|type="{}"} | |type="{}"} | ||
$U_{48} \ = \ $ { 0. } $\ \rm V $ | $U_{48} \ = \ $ { 0. } $\ \rm V $ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' In | + | '''(1)''' In each frame, $16$ bits of the base channels $\rm B1$ and $\rm B2$ are transmitted. |
| − | :$$R_{\rm B} = \frac{16\,\,{\rm bit}}{T_{\rm R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm R} = \frac{16\,\,{\rm bit}}{64 \cdot 10^3\,\,{\rm bit/s}} \hspace{0.15cm}\underline{= 250 \,{\rm \ | + | *With the frame duration $T_{\rm R}$, the bit rate $(R_{\rm B} = 64 \ \rm kbit/s)$ of each frame is thus: |
| + | :$$R_{\rm B} = \frac{16\,\,{\rm bit}}{T_{\rm R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm R} = \frac{16\,\,{\rm bit}}{64 \cdot 10^3\,\,{\rm bit/s}} \hspace{0.15cm}\underline{= 250 \,{\rm µ s}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(2)''' Thus, the following time duration is available for each of the $48$ bits: | ||
| + | :$$T_{\rm B} = \frac{T_{\rm R}}{48} = \frac{250 \,{\rm µ s}}{48} \hspace{0.15cm}\underline{ = 5.208 \,{\rm µ s}}$$ | ||
| + | *Since in (modified) AMI encoding each binary symbol is replaced by a ternary symbol of the same duration, the symbol duration after AMI encoding is also $T_{\rm B}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The gross data rate is equal to the reciprocal of the bit duration: | ||
| + | :$$R_{\rm gross} = \frac{1}{T_{\rm B}} \hspace{0.15cm}\underline{= 192 \,{\rm kbit/s}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(4)''' The number of control bits $\rm (CB)$ is: | ||
| + | :$$N_{\rm CB} = 48 - 2 \cdot 16 -4 \hspace{0.15cm}\underline{= 12} \hspace{0.05cm}.$$ | ||
| + | *These are marked in yellow in the graph. | ||
| + | |||
| + | *Thus, the total gross data rate calculated in the last subquestion is composed as follows: | ||
| + | :$$R_{\rm gross} = 2 \cdot {R_{\rm B}} + {R_{\rm D}} + {R_{\rm CB}} = 2 \cdot 64 \,{\rm kbit/s} + 16 \,{\rm kbit/s} + 48 \,{\rm kbit/s} = 192 \,{\rm kbit/s} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''( | + | '''(5)''' Note that the first "0" is encoded with positive polarity and all following alternating with $±0.75 \ {\rm V}$: |
| − | + | *$U_{1} = U_{5} = U_{9} = U_{12} =\text{ ...} = +0.75 \ {\rm V},$ | |
| − | + | *$ U_{2} = U_{7} = U_{10} = U_{13} = \text{ ...} = -0.75 \ {\rm V}$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | $\ \ \ | + | It follows further: |
| + | *Bit $b_{10} = 0$ is represented by $U_{10} \underline{= -0.75 \ \rm V}$, | ||
| + | |||
| + | *bit $b_{11} = 1$ by $U_{11} \underline{= 0 \ \rm V}$, | ||
| + | |||
| + | *bit $b_{12} = 0$ by $U_{12} \underline{= +0.75 \ \rm V}$. | ||
| − | |||
| − | + | '''(6)''' | |
| + | *The $\rm L$ bit has the task of keeping the AMI encoded signal $($over all $48$ ternary symbols$)$ DC-free. | ||
| − | + | *Since the binary symbol "0" has occurred $22$ times $($i.e. $11$ times each the voltage values $+0.75 \ \rm V$ and $-0.75 \ \rm V)$ and correspondingly $27$ times the binary symbol "1" $($voltage value $0 \ \rm V)$, $U_{48}\hspace{0.15cm}\underline{=0 \ \rm V}$ must be set. | |
| Line 98: | Line 122: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^1.2 ISDN Basic Access^]] |
Latest revision as of 16:51, 24 October 2022
The graphic shows the frame structure of the $\rm S_{0}$ interface. Each frame of duration $T_{\rm R}$ contains $48$ bits, among them:
- $16$ bits for the bearer channel $\rm B1$ $($light blue$)$,
- $16$ bits for the bearer channel $\rm B2$ $($dark blue$)$,
- $4$ bits for the data channel $\rm D$ $($green$)$.
The required control bits are shown in yellow.
For this exercise, it is specified that each of the two base channels $\rm B1$ and $\rm B2$ should provide a net data rate of $R_{\rm B} = 64 \ \rm kbit/s$.
It should also be noted that the bit duration $T_{\rm B}$ of the uncoded binary signal simultaneously indicates the symbol duration of the $($modified$)$ AMI code,
- which assigns each binary "$1$" to the voltage level $0 \ \rm V$ and
- alternately represents each binary "$0$" with $+0.75 \ \rm V$ resp. $–0.75 \ \rm V$.
The numerical values in the graphic $($marked in red$)$ indicate an example sequence which is to be converted into voltage levels in subtask (5) according to the modified AMI code.
- Bit number $48$ contains the so-called "$\rm L$ bit.
- This is to be set in subtask (6) in such a way that the signal $s(t)$ becomes DC–free.
Notes:
- This exercise is part of the chapter "ISDN Basic Access".
- The AMI code is described in detail in the chapter "Properties of the AMI code" of the book "Digital Signal Transmission".
- It should also be noted that the first $47$ bits contain exactly $22$ "zeros".
Questions
Solution
(1) In each frame, $16$ bits of the base channels $\rm B1$ and $\rm B2$ are transmitted.
- With the frame duration $T_{\rm R}$, the bit rate $(R_{\rm B} = 64 \ \rm kbit/s)$ of each frame is thus:
- $$R_{\rm B} = \frac{16\,\,{\rm bit}}{T_{\rm R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm R} = \frac{16\,\,{\rm bit}}{64 \cdot 10^3\,\,{\rm bit/s}} \hspace{0.15cm}\underline{= 250 \,{\rm µ s}} \hspace{0.05cm}.$$
(2) Thus, the following time duration is available for each of the $48$ bits:
- $$T_{\rm B} = \frac{T_{\rm R}}{48} = \frac{250 \,{\rm µ s}}{48} \hspace{0.15cm}\underline{ = 5.208 \,{\rm µ s}}$$
- Since in (modified) AMI encoding each binary symbol is replaced by a ternary symbol of the same duration, the symbol duration after AMI encoding is also $T_{\rm B}$.
(3) The gross data rate is equal to the reciprocal of the bit duration:
- $$R_{\rm gross} = \frac{1}{T_{\rm B}} \hspace{0.15cm}\underline{= 192 \,{\rm kbit/s}} \hspace{0.05cm}.$$
(4) The number of control bits $\rm (CB)$ is:
- $$N_{\rm CB} = 48 - 2 \cdot 16 -4 \hspace{0.15cm}\underline{= 12} \hspace{0.05cm}.$$
- These are marked in yellow in the graph.
- Thus, the total gross data rate calculated in the last subquestion is composed as follows:
- $$R_{\rm gross} = 2 \cdot {R_{\rm B}} + {R_{\rm D}} + {R_{\rm CB}} = 2 \cdot 64 \,{\rm kbit/s} + 16 \,{\rm kbit/s} + 48 \,{\rm kbit/s} = 192 \,{\rm kbit/s} \hspace{0.05cm}.$$
(5) Note that the first "0" is encoded with positive polarity and all following alternating with $±0.75 \ {\rm V}$:
- $U_{1} = U_{5} = U_{9} = U_{12} =\text{ ...} = +0.75 \ {\rm V},$
- $ U_{2} = U_{7} = U_{10} = U_{13} = \text{ ...} = -0.75 \ {\rm V}$.
It follows further:
- Bit $b_{10} = 0$ is represented by $U_{10} \underline{= -0.75 \ \rm V}$,
- bit $b_{11} = 1$ by $U_{11} \underline{= 0 \ \rm V}$,
- bit $b_{12} = 0$ by $U_{12} \underline{= +0.75 \ \rm V}$.
(6)
- The $\rm L$ bit has the task of keeping the AMI encoded signal $($over all $48$ ternary symbols$)$ DC-free.
- Since the binary symbol "0" has occurred $22$ times $($i.e. $11$ times each the voltage values $+0.75 \ \rm V$ and $-0.75 \ \rm V)$ and correspondingly $27$ times the binary symbol "1" $($voltage value $0 \ \rm V)$, $U_{48}\hspace{0.15cm}\underline{=0 \ \rm V}$ must be set.