Difference between revisions of "Aufgaben:Exercise 4.4: Extrinsic L-values at SPC"
| Line 9: | Line 9: | ||
:$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | :$$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$ | ||
| − | + | The extrinsic $L$ value over the $i$th code symbol reads with the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming–weight"]] $w_{\rm H}$ of the truncated sequence $\underline{x}^{(-i)}$: | |
:$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | :$$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *If the probability in the numerator is greater than that in the denominator, then $L_{\rm E}(i) > 0$ and thus the a posteriori–$L$– value $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ magnified, that is tends to be affected in the direction of the symbol $x_i = 0$ . |
| − | * | + | *If $L_{\rm E}(i) < 0$ from the point of view of the other symbols $(j ≠ i)$ there is much to be said for $x_i = 1$ . |
| − | + | Only the $\text{SPC (4, 3, 4)}$ is treated, where for the probabilities $p_i = {\rm Pr}(x_i = 1)$ holds: | |
:$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} | :$$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} | ||
p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} | p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} | ||
| Line 23: | Line 23: | ||
p_4 = 0.6 \hspace{0.05cm}.$$ | p_4 = 0.6 \hspace{0.05cm}.$$ | ||
| − | + | From this the apriori–$L$ values result to: | |
:$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} | :$$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} | ||
\right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} | ||
| Line 36: | Line 36: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder|"Soft–in Soft–out Decoder"]]. |
| − | * | + | *Reference is made in particular to the page [[Channel_Coding/Soft-in_Soft-Out_Decoder#Calculation_of_extrinsic_LLRs|"Calculation of the extrinsic $L$ values"]]. |
| − | * In | + | * In the table are given for $p_i = 0$ to $p_i = 1$ with step size $0.1$ (column 1): |
| − | ::In | + | ::In column 2: the probability $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$, |
| − | ::in | + | ::in column 3: the values for $1 - 2p_i$, |
| − | ::in | + | ::in column 4: the apriori $L$ values $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$. |
| − | * | + | * The <i>hyperbolic tangent</i> ($\tanh$) of $L_i/2$ is identical to $1-2p_i$ ⇒ column 3. |
| − | * In | + | * In the [[Aufgaben:Exercise_4.4Z:_Supplement_to_Exercise_4.4|"Exercise 4.4Z"]] it is shown that for the extrinsic $L$–value can also be written: |
:$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | ||
{\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) | {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) | ||
| Line 51: | Line 51: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {It holds $p_1 = 0.2, \ p_2 = 0.9, \ p_3 = 0.3, \ p_4 = 0.6$. From this, calculate the apriori $L$ values of the $\text{SPC (4, 3, 4)}$ for bit 1 and bit 2. |
|type="{}"} | |type="{}"} | ||
$L_{\rm A}(i = 1) \ = \ ${ 1.386 3% } | $L_{\rm A}(i = 1) \ = \ ${ 1.386 3% } | ||
$L_{\rm A}(i = 2) \ = \ ${ -2.26291--2.13109 } | $L_{\rm A}(i = 2) \ = \ ${ -2.26291--2.13109 } | ||
| − | { | + | {What are the extrinsic $L$ values for bit 1 and bit 2. |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(i = 1) \ = \ ${ 0.128 3% } | $L_{\rm E}(i = 1) \ = \ ${ 0.128 3% } | ||
$L_{\rm E}(i = 2) \ = \ ${ -0.09888--0.09312 } | $L_{\rm E}(i = 2) \ = \ ${ -0.09888--0.09312 } | ||
| − | { | + | {What are the relationships between $p_j$ and $L_j = L_{\rm A}(j)$? |
|type="[]"} | |type="[]"} | ||
+ Es gilt $p_j = 1/(1 + {\rm e}^ {L_j})$. | + Es gilt $p_j = 1/(1 + {\rm e}^ {L_j})$. | ||
| Line 69: | Line 69: | ||
+ Es gilt $1-2p_j = \tanh {(L_j/2)}$. | + Es gilt $1-2p_j = \tanh {(L_j/2)}$. | ||
| − | { | + | {It further $p_1 = 0.2, \ p_2 = 0.9, \ p_3$ and $p_4 = 0.6$. Calculate the extrinsic $L$ values for bit 3 and bit 4. <br>Use different equations for this purpose. |
|type="{}"} | |type="{}"} | ||
$L_{\rm E}(i = 3) \ = \ ${ 0.193 3% } | $L_{\rm E}(i = 3) \ = \ ${ 0.193 3% } | ||
| Line 75: | Line 75: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the apriori $L$ values of the first two bits of the code word: |
:$$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} | :$$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 83: | Line 83: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | The values can be read from the fourth column of the table attached to the information page. | |
| − | '''(2)''' | + | '''(2)''' To calculate the extrinsic $L$ value over the $i$th bit, only the information about the other three bits $(j ≠ i)$ may be used. With the given equation holds: |
:$$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} | :$$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *For the product, we obtain according to the third column of [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|"table"]]: |
:$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 | (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 | ||
| Line 97: | Line 97: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *In terms of bit 2, one obtains accordingly: |
:$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 | (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 | ||
| Line 105: | Line 105: | ||
| − | '''(3)''' | + | '''(3)''' For the apriori $L$ value holds: |
:$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} | :$$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} | ||
\right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} | \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} | ||
| Line 113: | Line 113: | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | * | + | *Thus also applies: |
:$$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } | :$$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } | ||
= \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$ | = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$ | ||
| − | * | + | *Multiplying the numerator and denominator by ${\rm e}^{-L_j/2}$, we get: |
:$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$ | :$$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$ | ||
| − | * | + | *Thus <u>all proposed solutions</u> are correct. |
| − | * | + | *The function <i>hyperbolic tangent</i> can be found, for example, in tabular form in collections of formulas or in the last column of the table given in front. |
| − | '''(4)''' | + | '''(4)''' We first calculate $L_{\rm E}(i = 3)$ in the same way as in subtask (2): |
:$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | :$$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = | ||
(+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 | (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 | ||
| Line 131: | Line 131: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *We calculate the extrinsic $L$ value with respect to the last bit according to the equation |
:$$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | :$$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} | ||
{\rm mit} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) | {\rm mit} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *This results in accordance with the above [[Aufgaben:Exercise_4.4:_Extrinsic_L-values_at_SPC|"table"]]: |
:$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | :$$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} | ||
| Line 156: | Line 156: | ||
= 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$ | = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$ | ||
| − | * | + | *The final result is thus: |
:$$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 | :$$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
Revision as of 18:44, 29 October 2022
We consider again the "single parity–check code". In such a ${\rm SPC} \ (n, \, n-1, \, 2)$ the $n$ bits of a codeword $\underline{x}$ come from the $k = n -1$ bits from the source sequence $\underline{u}$ and only a single check bit $p$ is added, such that the number of ones in the codeword is even:
- $$\underline{x} = \big ( \hspace{0.03cm}x_1, \hspace{0.03cm} x_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n-1}, \hspace{0.03cm} x_n \hspace{0.03cm} \big ) = \big ( \hspace{0.03cm}u_1, \hspace{0.03cm} u_2, \hspace{0.05cm} \text{...} \hspace{0.05cm} , u_{k}, \hspace{0.03cm} p \hspace{0.03cm} \big )\hspace{0.03cm}. $$
The extrinsic information about the $i$th code bit is formed over all other symbols $(j ≠ i)$ . Therefore we write for the code word shorter by one bit:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{0.05cm} \text{...} \hspace{0.05cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
The extrinsic $L$ value over the $i$th code symbol reads with the "Hamming–weight" $w_{\rm H}$ of the truncated sequence $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
- If the probability in the numerator is greater than that in the denominator, then $L_{\rm E}(i) > 0$ and thus the a posteriori–$L$– value $L_{\rm APP}(i) = L_{\rm A}(i) + L_{\rm E}(i)$ magnified, that is tends to be affected in the direction of the symbol $x_i = 0$ .
- If $L_{\rm E}(i) < 0$ from the point of view of the other symbols $(j ≠ i)$ there is much to be said for $x_i = 1$ .
Only the $\text{SPC (4, 3, 4)}$ is treated, where for the probabilities $p_i = {\rm Pr}(x_i = 1)$ holds:
- $$p_1 = 0.2 \hspace{0.05cm}, \hspace{0.3cm} p_2 = 0.9 \hspace{0.05cm}, \hspace{0.3cm} p_3 = 0.3 \hspace{0.05cm}, \hspace{0.3cm} p_4 = 0.6 \hspace{0.05cm}.$$
From this the apriori–$L$ values result to:
- $$L_{\rm A}(i) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_i = 0)}{{\rm Pr}(x_i = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_i}{p_i} \right ] \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the page "Calculation of the extrinsic $L$ values".
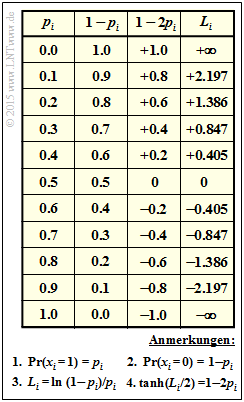
- In the table are given for $p_i = 0$ to $p_i = 1$ with step size $0.1$ (column 1):
- In column 2: the probability $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$,
- in column 3: the values for $1 - 2p_i$,
- in column 4: the apriori $L$ values $L_i = \ln {\big [(1 - p_i)/p_ i \big ]} = L_{\rm A}(i)$.
- The hyperbolic tangent ($\tanh$) of $L_i/2$ is identical to $1-2p_i$ ⇒ column 3.
- In the "Exercise 4.4Z" it is shown that for the extrinsic $L$–value can also be written:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = \prod\limits_{j \ne i}^{n} \hspace{0.25cm}(1-2p_j) \hspace{0.05cm}.$$
Questions
Solution
- $$L_{\rm A}(i = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_1}{p_1} \right ] = {\rm ln} \hspace{0.1cm} 4 \hspace{0.15cm}\underline{= +1.386} \hspace{0.05cm},$$
- $$L_{\rm A}(i = 2) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_2}{p_2} \right ] = {\rm ln} \hspace{0.1cm} 1/9 \hspace{0.15cm}\underline{= -2.197} \hspace{0.05cm}.$$
The values can be read from the fourth column of the table attached to the information page.
(2) To calculate the extrinsic $L$ value over the $i$th bit, only the information about the other three bits $(j ≠ i)$ may be used. With the given equation holds:
- $$L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)}{1 - \prod\limits_{j \ne 1} \hspace{0.25cm}(1-2p_j)} \hspace{0.05cm}.$$
- For the product, we obtain according to the third column of "table":
- $$\prod\limits_{j =2, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.064 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 1) = {\rm ln} \hspace{0.2cm} \frac{1 + 0.064}{1 - 0.064} = {\rm ln} \hspace{0.1cm} (1.137)\hspace{0.15cm}\underline{= +0.128} \hspace{0.05cm}.$$
- In terms of bit 2, one obtains accordingly:
- $$\prod\limits_{j =1, \hspace{0.05cm}3,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (+0.4) \cdot (-0.2) = -0.048 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 2) = {\rm ln} \hspace{0.2cm} \frac{1 -0.048}{1 +0.048} = {\rm ln} \hspace{0.1cm} (0.908)\hspace{0.15cm}\underline{= -0.096} \hspace{0.05cm}.$$
(3) For the apriori $L$ value holds:
- $$L_j = L_{\rm A}(j) = {\rm ln} \hspace{0.1cm} \left [ \frac{{\rm Pr}(x_j = 0)}{{\rm Pr}(x_j = 1)} \right ] = {\rm ln} \hspace{0.1cm} \left [ \frac{1-p_j}{p_j} \right ]\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_j = p_j \cdot {\rm e}^{L_j} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_j = \frac{1}{1+{\rm e}^{L_j} } \hspace{0.05cm} .$$
- Thus also applies:
- $$1- 2 \cdot p_j = 1 - \frac{2}{1+{\rm e}^{L_j} } = \frac{1+{\rm e}^{L_j}-2}{1+{\rm e}^{L_j} } = \frac{{\rm e}^{L_j}-1}{{\rm e}^{L_j} +1}\hspace{0.05cm} .$$
- Multiplying the numerator and denominator by ${\rm e}^{-L_j/2}$, we get:
- $$1- 2 \cdot p_j = \frac{{\rm e}^{L_j/2}-{\rm e}^{-L_j/2}}{{\rm e}^{L_j/2}+{\rm e}^{-L_j/2}}={\rm tanh} (L_j/2) \hspace{0.05cm} .$$
- Thus all proposed solutions are correct.
- The function hyperbolic tangent can be found, for example, in tabular form in collections of formulas or in the last column of the table given in front.
(4) We first calculate $L_{\rm E}(i = 3)$ in the same way as in subtask (2):
- $$\prod\limits_{j =1, \hspace{0.05cm}2,\hspace{0.05cm} 4} \hspace{0.05cm}(1-2p_j) = (+0.6) \cdot (-0.8) \cdot (-0.2) = +0.096 \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}L_{\rm E}(i = 3) = {\rm ln} \hspace{0.2cm} \frac{1 +0.096}{1 -0.096} = {\rm ln} \hspace{0.1cm} (1.212)\hspace{0.15cm}\underline{= +0.193} \hspace{0.05cm}.$$
- We calculate the extrinsic $L$ value with respect to the last bit according to the equation
- $$L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 + \pi}{1 - \pi}\hspace{0.05cm}, \hspace{0.3cm} {\rm mit} \hspace{0.3cm} \pi = {\rm tanh}(L_1/2) \cdot {\rm tanh}(L_2/2) \cdot {\rm tanh}(L_3/2) \hspace{0.05cm}.$$
- This results in accordance with the above "table":
- $$p_1 = 0.2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1 = +1.386 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_1/2 = +0.693 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_1/2) = \frac{{\rm e}^{+0.693}-{\rm e}^{-0.693}}{{\rm e}^{+0.693}+{\rm e}^{-0.693}} = 0.6 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_1\hspace{0.05cm},$$
- $$p_2 = 0.9 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2 = -2.197 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_2/2 = -1.099\hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_2/2) = \frac{{\rm e}^{-1.099}-{\rm e}^{+1.099}}{{\rm e}^{-1.099}+{\rm e}^{+1.099}} = -0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_2\hspace{0.05cm},$$
- $$p_3 = 0.3 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3 = 0.847 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} L_3/2 = +0.419 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm tanh}(L_3/2) = \frac{{\rm e}^{+0.419}-{\rm e}^{-0.419}}{{\rm e}^{+0.419}+{\rm e}^{-0.419}} = 0.4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm identisch \hspace{0.15cm}mit\hspace{0.15cm} }1-2\cdot p_3\hspace{0.05cm}.$$
- The final result is thus:
- $$\pi = (+0.6) \cdot (-0.8) \cdot (+0.4) = -0.192 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} L_{\rm E}(i = 4) = {\rm ln} \hspace{0.2cm} \frac{1 -0.192}{1 +0.192}\hspace{0.15cm}\underline{= -0.389} \hspace{0.05cm}.$$