Difference between revisions of "Aufgaben:Exercise 4.7: Product Code Decoding"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/The_Basics_of_Product_Codes}} |
| − | [[File:P_ID3006__KC_A_4_7_v2.png|right|frame| | + | [[File:P_ID3006__KC_A_4_7_v2.png|right|frame|Syndrome tables of the considered component codes $\mathcal{C}_1$ and $\mathcal{C}_2$]] |
| − | + | We consider, as in the [[Aufgaben:Aufgabe_4.6:_Produktcode–Generierung|"Exercise 4.6"]] a product code based on. | |
| − | * | + | * the Hamming code $\rm HC \ (7, \ 4, \ 3)$ ⇒ $\mathcal{C}_1$, |
| − | * | + | * the truncated Hamming code $\rm HC \ (6, \ 3, \ 3)$ ⇒ $\mathcal{C}_2$. |
| − | + | The parity-check matrices of these component codes are: | |
:$${ \boldsymbol{\rm H}}_1 | :$${ \boldsymbol{\rm H}}_1 | ||
= \begin{pmatrix} | = \begin{pmatrix} | ||
| Line 21: | Line 21: | ||
\end{pmatrix} \hspace{0.05cm}.$$ | \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | + | For the sake of completeness, the generator matrices are also given, but they are not needed to solve the exercise: | |
:$${ \boldsymbol{\rm G}}_1 | :$${ \boldsymbol{\rm G}}_1 | ||
= \begin{pmatrix} | = \begin{pmatrix} | ||
| Line 36: | Line 36: | ||
\end{pmatrix} \hspace{0.05cm}.$$ | \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | + | The <i>Hard Decision Decoding</i> of this code is preferably done iteratively, by alternately syndromdecoding all rows and then all columns. See: [[Channel_Coding/The_Basics_of_Product_Codes#Iterative_syndrome_decoding_of_product_codes| "Iterative Syndrome Decoding of Product Codes"]]. | |
| − | + | Syndrome decoding of (one-dimensional) block codes has already been covered in the chapter [[Channel_Coding/Decoding_of_Linear_Block_Codes| "Decoding of Linear Block Codes"]] . Here is a brief summary and an adaptation to the two-dimensional case: | |
| − | * | + | * From the received word $\underline{y}$ (a row or a column of the given received matrix), the syndrome corresponding to $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$ respectively $\underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T}$ formed. |
| − | * | + | *With the result $\underline{s} = \underline{s}_{\mu}$ one can read in above tables the so called side class adder $\underline{e}_{\mu}$ . |
| − | * | + | *The corrected codeword is then $\underline{y} + \underline{e}_{\mu}$. |
| − | [[File:P_ID3007__KC_A_4_7zusatz_v1.png|right|frame| | + | [[File:P_ID3007__KC_A_4_7zusatz_v1.png|right|frame|Predefined coder and receiver matrices]] |
| − | <br><br><br> | + | <br><br><br>The accompanying diagram shows three different coder– and receiver matrices to be analyzed in the subtasks '''(1)''', '''(2)''', and '''(3)''': |
| − | * | + | *We name them constellation $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$. |
| − | * | + | *Marked in yellow are the differences in the reception matrix of constellation $\mathbf{B}$ versus $\mathbf{A}$. |
| − | *In | + | *In both cases, the code matrix consists only of zeros. |
| − | * | + | *The code matrix of $\rm C$ was determined in the [[Aufgaben:Aufgabe_4.6:_Produktcode–Generierung|Aufgabe 4.6]] . |
| Line 56: | Line 56: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Channel_Coding/The_Basics_of_Product_Codes| "Basics of Product Codes"]]. |
| − | * | + | *Reference is made in particular to the page [[Channel_Coding/The_Basics_of_Product_Codes#Iterative_syndrome_decoding_of_product_codes| "Iterative syndrome decoding of product codes"]]. |
| Line 64: | Line 64: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Is the two-dimensional received matrix $\mathbf{A}$ decodable? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes, after the first decoding in horizontal direction. |
| − | - | + | - Yes, after the first decoding in vertical direction. |
| − | + | + | + Yes, after the second decoding in horizontal direction. |
| − | - | + | - Yes, after the second decoding in vertical direction. |
| − | - | + | - No. |
| − | { | + | {Is the two-dimensional received matrix $\mathbf{B}$ decodable? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes, after the first decoding in horizontal direction. |
| − | - | + | - Yes, after the first decoding in vertical direction. |
| − | + | + Yes, after the second decoding in horizontal direction. | |
| − | - | + | - Yes, after the second decoding in vertical direction. |
| − | + | - No. | |
| − | { | + | {Is the two-dimensional received matrix $\mathbf{C}$ decodable? Try to find the solution via an equivalence to the exercise '''(1)''' or '''(2)'''. |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes, after the first decoding in horizontal direction. |
| − | - | + | - Yes, after the first decoding in vertical direction. |
| − | + | + | + Yes, after the second decoding in horizontal direction. |
| − | - | + | - Yes, after the second decoding in vertical direction. |
| − | - | + | - No. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The decoding process of the receive matrix $\mathbf{A}$ is illustrated by the following diagram. |
| − | [[File:P_ID3008__KC_A_4_7a_v1.png|center|frame| | + | [[File:P_ID3008__KC_A_4_7a_v1.png|center|frame|Syndrome decoding of the two-dimensional received matrix $\mathbf{A}$.]] |
| − | * | + | * The single errors in rows 1, 3, 5 and 6 are detected by $(7, \ 4, \ 3)$–Hamming code and can be corrected <br> ⇒ green markings in the graphic "1st iteration horizontal". |
| − | * | + | * For the second row results the syndrome |
:$$\underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} | :$$\underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} | ||
\begin{pmatrix} | \begin{pmatrix} | ||
| Line 114: | Line 114: | ||
= \underline{s}_1 \hspace{0.03cm}.$$ | = \underline{s}_1 \hspace{0.03cm}.$$ | ||
| − | * | + | * According to the upper syndrome table on the information page, the last bit is thus incorrectly "corrected". Incorrect corrections are entered in red in the upper graphic. |
| − | * | + | * Correspondingly applies to the fourth row: |
:$$\underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = | :$$\underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = | ||
\left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) | \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) | ||
+ \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= | + \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= | ||
\left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.$$ | \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.$$ | ||
| − | * | + | * This causes a miscorrection of bit 5. |
| − | :* | + | :* Vertical decoding of columns 1, 3, 4, 5, 6, and 7 is straightforward because there is at most one error per column, which can be corrected by the truncated Hamming code $\rm (6, \ 3, \ 3)$. |
| − | :* In | + | :* In column 2, however, there is a miscorrection of the last bit according to the lower syndrome table. With the transpose of the $\rm (6, \ 3, \ 3)$ parity-check matrix $\mathbf{H}_2$ results namely: |
:$$\underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} | :$$\underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} | ||
= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot | = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot | ||
| Line 138: | Line 138: | ||
+ \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= | + \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= | ||
\left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.$$ | \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.$$ | ||
| − | * | + | * The second horizontal decoding is problem-free, since now at most one error occurs in each row ⇒ <u>Solution suggestion 3</u>. |
| − | '''(2)''' | + | '''(2)''' The following graphic shows the decoding process according to the specifications given by $\mathbf{B}$. |
| − | [[File:P_ID3009__KC_A_4_7b_v2.png|center|frame| | + | [[File:P_ID3009__KC_A_4_7b_v2.png|center|frame|For syndrome decoding of the two-dimensional receive matrix $\mathbf{B}$.]] |
| − | + | Despite only minor modifications compared to $\mathbf{A}$, there are now serious differences: | |
| − | * | + | * Due to the first horizontal decoding, the "corrected" rows 2 and 4 now read equally: $(0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1)$, i.e., the last bit of these rows is miscorrected in each case. |
| − | * | + | * Vertical decoding results in identical columns 2, 4, and 6, namely $(0, \, 1, \, 0, \, 1, \, 0, \, 1)$. After that, there are three ones (or none) in each row and in each column. |
| − | * | + | * This constellation remains for arbitrary further (horizontal or vertical) decodings, because for $d_{\rm min} = 3$ always the syndrome $\underline{s}_0 = (0, \, 0, \, 0)$ results. |
| − | + | The correct solution is <u>proposal 5</u>. | |
| − | '''(3)''' | + | '''(3)''' Comparing the coder– and receiver matrices (differences are marked in blue), one can create the error matrix by modulo 2 additions according to the following graph. |
| − | [[File:P_ID3010__KC_A_4_7c_v2.png|center|frame| | + | [[File:P_ID3010__KC_A_4_7c_v2.png|center|frame|Matrix representation of coder, receiver and error pattern]] |
| − | + | The error matrix is equal to the receive matrix of $\mathbf{A}$ ⇒ again, <u>proposed solution 3</u> is correct. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | |||
[[Category:Channel Coding: Exercises|^4.2 About the Product Codes^]] | [[Category:Channel Coding: Exercises|^4.2 About the Product Codes^]] | ||
Revision as of 17:58, 31 October 2022
We consider, as in the "Exercise 4.6" a product code based on.
- the Hamming code $\rm HC \ (7, \ 4, \ 3)$ ⇒ $\mathcal{C}_1$,
- the truncated Hamming code $\rm HC \ (6, \ 3, \ 3)$ ⇒ $\mathcal{C}_2$.
The parity-check matrices of these component codes are:
- $${ \boldsymbol{\rm H}}_1 = \begin{pmatrix} 1 &1 &0 &1 &1 &0 &0 \\ 0 &1 &1 &1 &0 &1 &0 \\ 1 &0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm H}}_2 = \begin{pmatrix} 1 &1 &0 &1 &0 &0 \\ 1 &0 &1 &0 &1 &0 \\ 0 &1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
For the sake of completeness, the generator matrices are also given, but they are not needed to solve the exercise:
- $${ \boldsymbol{\rm G}}_1 = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1 \\ 0 &1 &0 &0 &1 &1 &0 \\ 0 &0 &1 &0 &0 &1 &1 \\ 0 &0 &0 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.8cm} { \boldsymbol{\rm G}}_2 = \begin{pmatrix} 1 &0 &0 &1 &1 &0 \\ 0 &1 &0 &1 &0 &1 \\ 0 &0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.$$
The Hard Decision Decoding of this code is preferably done iteratively, by alternately syndromdecoding all rows and then all columns. See: "Iterative Syndrome Decoding of Product Codes".
Syndrome decoding of (one-dimensional) block codes has already been covered in the chapter "Decoding of Linear Block Codes" . Here is a brief summary and an adaptation to the two-dimensional case:
- From the received word $\underline{y}$ (a row or a column of the given received matrix), the syndrome corresponding to $\underline{s} = \underline{y} \cdot \mathbf{H}_1^{\rm T}$ respectively $\underline{s} = \underline{y} \cdot \mathbf{H}_2^{\rm T}$ formed.
- With the result $\underline{s} = \underline{s}_{\mu}$ one can read in above tables the so called side class adder $\underline{e}_{\mu}$ .
- The corrected codeword is then $\underline{y} + \underline{e}_{\mu}$.
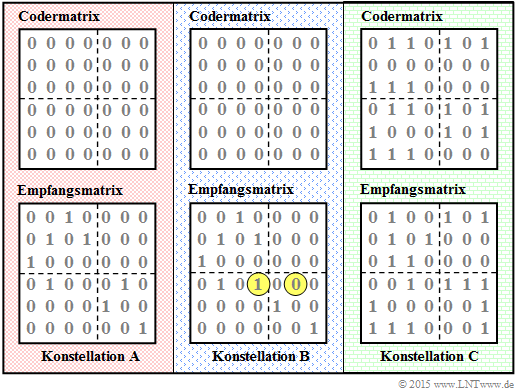
The accompanying diagram shows three different coder– and receiver matrices to be analyzed in the subtasks (1), (2), and (3):
- We name them constellation $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$.
- Marked in yellow are the differences in the reception matrix of constellation $\mathbf{B}$ versus $\mathbf{A}$.
- In both cases, the code matrix consists only of zeros.
- The code matrix of $\rm C$ was determined in the Aufgabe 4.6 .
Hints:
- This exercise belongs to the chapter "Basics of Product Codes".
- Reference is made in particular to the page "Iterative syndrome decoding of product codes".
Questions
Solution
- The single errors in rows 1, 3, 5 and 6 are detected by $(7, \ 4, \ 3)$–Hamming code and can be corrected
⇒ green markings in the graphic "1st iteration horizontal". - For the second row results the syndrome
- $$\underline{s} = \underline{y}_2 \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \hspace{-0.05cm} \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1 \hspace{0.03cm}.$$
- According to the upper syndrome table on the information page, the last bit is thus incorrectly "corrected". Incorrect corrections are entered in red in the upper graphic.
- Correspondingly applies to the fourth row:
- $$\underline{s} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0 \right ) \cdot { \boldsymbol{\rm H}}_1^{\rm T} = \left ( 1, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right ) + \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0 \right )= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \underline{s}_4 \hspace{0.05cm}.$$
- This causes a miscorrection of bit 5.
- Vertical decoding of columns 1, 3, 4, 5, 6, and 7 is straightforward because there is at most one error per column, which can be corrected by the truncated Hamming code $\rm (6, \ 3, \ 3)$.
- In column 2, however, there is a miscorrection of the last bit according to the lower syndrome table. With the transpose of the $\rm (6, \ 3, \ 3)$ parity-check matrix $\mathbf{H}_2$ results namely:
- $$\underline{s}= \underline{y}_{2{\rm S}}\cdot { \boldsymbol{\rm H}}_2^{\rm T} = \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}0, \hspace{0.03cm}1, \hspace{0.03cm}0, \hspace{0.03cm}0 \right ) \cdot \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) + \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right )= \left ( 0, \hspace{0.03cm} 0, \hspace{0.03cm}1 \right ) = \underline{s}_1.$$
- The second horizontal decoding is problem-free, since now at most one error occurs in each row ⇒ Solution suggestion 3.
(2) The following graphic shows the decoding process according to the specifications given by $\mathbf{B}$.
Despite only minor modifications compared to $\mathbf{A}$, there are now serious differences:
- Due to the first horizontal decoding, the "corrected" rows 2 and 4 now read equally: $(0, \, 1, \, 0, \, 1, \, 0, \, 0, \, 1)$, i.e., the last bit of these rows is miscorrected in each case.
- Vertical decoding results in identical columns 2, 4, and 6, namely $(0, \, 1, \, 0, \, 1, \, 0, \, 1)$. After that, there are three ones (or none) in each row and in each column.
- This constellation remains for arbitrary further (horizontal or vertical) decodings, because for $d_{\rm min} = 3$ always the syndrome $\underline{s}_0 = (0, \, 0, \, 0)$ results.
The correct solution is proposal 5.
(3) Comparing the coder– and receiver matrices (differences are marked in blue), one can create the error matrix by modulo 2 additions according to the following graph.
The error matrix is equal to the receive matrix of $\mathbf{A}$ ⇒ again, proposed solution 3 is correct.