Difference between revisions of "Aufgaben:Exercise 2.10: Shannon-Fano Coding"
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Further_Source_Coding_Methods |
}} | }} | ||
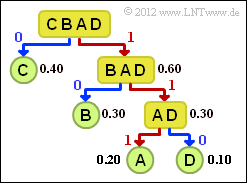
[[File:P_ID2465__Inf_A_2_10.png |right|frame|Tree diagram of the <br>Shannon-Fano coding]] | [[File:P_ID2465__Inf_A_2_10.png |right|frame|Tree diagram of the <br>Shannon-Fano coding]] | ||
| − | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano] | + | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano], which is described in the theory section. |
| − | This special type of source coding will be described here using a simple example for the symbol | + | This special type of source coding will be described here using a simple example for the symbol set size $M = 4$ and the following symbol probabilities: |
:$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | ||
| Line 17: | Line 17: | ||
:2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$. | :2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$. | ||
| − | :3. The binary symbol <b>0</b>is assigned to the less probable group, <b>1</b> to the other group. | + | :3. The binary symbol <b>0</b> is assigned to the less probable group, <b>1</b> to the other group. |
:4. If there is more than one symbol in a group, the algorithm is to be applied recursively. | :4. If there is more than one symbol in a group, the algorithm is to be applied recursively. | ||
| − | For this example, the following code assignment results (in the tree diagram, a red connection marks a <b>1</b> and a blue one a <b>0</b>: | + | For this example, the following code assignment results (in the tree diagram, a red connection marks a <b>1</b> and a blue one a <b>0</b>): |
: $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | : $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | ||
| − | This gives the following for the | + | This gives the following for the average code word length: |
| − | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\ | + | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$ |
The Huffman algorithm would produce a slightly different code here, but even in this case | The Huffman algorithm would produce a slightly different code here, but even in this case | ||
| − | *$\rm C$ is | + | *$\rm C$ is encoded with one bit, |
*$\rm B$ with two bits and | *$\rm B$ with two bits and | ||
*$\rm A$ and $\rm D$ with three bits each. | *$\rm A$ and $\rm D$ with three bits each. | ||
| − | This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\ | + | This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\hspace{0.15cm}symbol$. |
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities | In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities | ||
:$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | ||
| − | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$ | + | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09.$$ |
| − | + | You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency. | |
With the Huffman code, the following assignment results with the probabilities at hand: | With the Huffman code, the following assignment results with the probabilities at hand: | ||
| Line 54: | Line 54: | ||
| − | + | Hints: | |
| − | *The assignment belongs to the chapter [[Information_Theory/Weitere_Quellencodierverfahren| | + | *The assignment belongs to the chapter [[Information_Theory/Weitere_Quellencodierverfahren|Further source coding methods]]. |
*In particular, reference is made to the page [[Information_Theory/Weitere_Quellencodierverfahren#The_Shannon-Fano_algorithm|The Shannon-Fano algorithm]]. | *In particular, reference is made to the page [[Information_Theory/Weitere_Quellencodierverfahren#The_Shannon-Fano_algorithm|The Shannon-Fano algorithm]]. | ||
| − | *To check your results, please refer to the | + | *To check your results, please refer to the (German language) SWF module [[Applets:Huffman_Shannon_Fano|Coding according to Huffman and Shannon/Fano]]. |
| Line 65: | Line 65: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the | + | {What is the average code word length $L_{\rm M}$ for the <u>Huffman code</u>? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/source\ | + | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
| − | {What happens in the first step of <u>Shannon–Fano coding</u>? | + | {What happens in the first step of <u>Shannon–Fano coding</u>? <u>Hint</u>: All other symbols are grouped together in the second group. |
| − | |type=" | + | |type="()"} |
- $\rm A$ and $\rm B$ are combined into the first group. | - $\rm A$ and $\rm B$ are combined into the first group. | ||
+ $\rm B$ and $\rm E$ are combined into the first group. | + $\rm B$ and $\rm E$ are combined into the first group. | ||
| Line 79: | Line 79: | ||
{Which assignments result for the <u>Shannon–Fano algorithm</u>? | {Which assignments result for the <u>Shannon–Fano algorithm</u>? | ||
|type="[]"} | |type="[]"} | ||
| − | + The character $\rm A$ is binary | + | + The character $\rm A$ is binary encoded with <b>010</b> . |
| − | + The character $\rm B$ is binary | + | + The character $\rm B$ is binary encoded with <b>11</b> . |
| − | + The character $\rm C$ is binary | + | + The character $\rm C$ is binary encoded with <b>00110</b> . |
| − | {What is the average | + | {What is the average code word length $L_{\rm M}$ for <u>Shannon–Fano code</u>? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/source\ | + | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
{Which statements are true for arbitrary probabilities? | {Which statements are true for arbitrary probabilities? | ||
|type="[]"} | |type="[]"} | ||
| − | - $L_{\rm M}$ could be smaller for "Shannon–Fano" than for "Huffman". | + | - $L_{\rm M}$ could be smaller for "Shannon–Fano" than for "Huffman". |
| − | + $L_{\rm M}$ could be larger at "Shannon–Fano" than at "Huffman". | + | + $L_{\rm M}$ could be larger at "Shannon–Fano" than at "Huffman". |
| − | + $L_{\rm M}$ could be the same for "Shannon–Fano" and "Huffman". | + | + $L_{\rm M}$ could be the same for "Shannon–Fano" and "Huffman". |
| Line 102: | Line 102: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' For the given Huffman code one obtains: | '''(1)''' For the given Huffman code one obtains: | ||
| − | :$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\ | + | :$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\hspace{0.15cm}symbol}}\hspace{0.05cm}. $$ |
| Line 110: | Line 110: | ||
*All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step: | *All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step: | ||
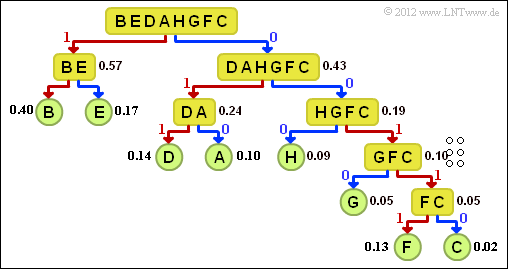
| + | [[File:P_ID2466__Inf_A_2_10c.png|right|frame|Tree diagram of Shannon-Fano coding]] | ||
:$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | ||
| − | |||
*With the distribution according to solution suggestion 3, the equal distribution would be achieved even less: | *With the distribution according to solution suggestion 3, the equal distribution would be achieved even less: | ||
:$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| Line 127: | Line 125: | ||
'''(4)''' Using the result of sub-task '''(3)''' , we get: | '''(4)''' Using the result of sub-task '''(3)''' , we get: | ||
| − | :$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\ | + | :$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\hspace{0.15cm}symbol}}\hspace{0.05cm}. $$ |
| Line 133: | Line 131: | ||
'''(5)''' <u>Statements 2 and 3</u> are correct: | '''(5)''' <u>Statements 2 and 3</u> are correct: | ||
*In the present example, Shannon-Fano results in a less favourable value than Huffman. | *In the present example, Shannon-Fano results in a less favourable value than Huffman. | ||
| − | *In most cases – including the example on the information page – Huffman and Shannon-Fano result in an equivalent code and thus also the same average code word length. | + | *In most cases – including the example on the information page – "Huffman" and "Shannon-Fano" result in an equivalent code and thus also to the same average code word length. |
*Shannon-Fano, on the other hand, never delivers a more effective code than Huffman. | *Shannon-Fano, on the other hand, never delivers a more effective code than Huffman. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:05, 1 November 2022
Another algorithm for entropy coding was given in 1949 by Claude Elwood Shannon and Robert Fano, which is described in the theory section.
This special type of source coding will be described here using a simple example for the symbol set size $M = 4$ and the following symbol probabilities:
- $$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$
The graph shows the corresponding tree diagram. Proceed as follows:
- 1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.
- 2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$.
- 3. The binary symbol 0 is assigned to the less probable group, 1 to the other group.
- 4. If there is more than one symbol in a group, the algorithm is to be applied recursively.
For this example, the following code assignment results (in the tree diagram, a red connection marks a 1 and a blue one a 0):
- $\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.
This gives the following for the average code word length:
- $$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$
The Huffman algorithm would produce a slightly different code here, but even in this case
- $\rm C$ is encoded with one bit,
- $\rm B$ with two bits and
- $\rm A$ and $\rm D$ with three bits each.
This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\hspace{0.15cm}symbol$.
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities
- $$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09.$$
You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency.
With the Huffman code, the following assignment results with the probabilities at hand:
- $\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.
Hints:
- The assignment belongs to the chapter Further source coding methods.
- In particular, reference is made to the page The Shannon-Fano algorithm.
- To check your results, please refer to the (German language) SWF module Coding according to Huffman and Shannon/Fano.
Questions
Solution
- $$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\hspace{0.15cm}symbol}}\hspace{0.05cm}. $$
(2) The correct answer is 2:
- Before applying the Shannon-Fano algorithm, the characters must first be sorted according to their occurrence probabilities. Thus, answer 1 is incorrect.
- All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step:
- $${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$
- With the distribution according to solution suggestion 3, the equal distribution would be achieved even less:
- $${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$
(3) All suggeted solutionss are correct:
- The graph shows the tree diagram of the Shannon-Fano coding.
- This results in the following assignment (a red connection indicates a 1 , a blue one indicates a 0):
- $\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,
- ${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.
(4) Using the result of sub-task (3) , we get:
- $$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\hspace{0.15cm}symbol}}\hspace{0.05cm}. $$
(5) Statements 2 and 3 are correct:
- In the present example, Shannon-Fano results in a less favourable value than Huffman.
- In most cases – including the example on the information page – "Huffman" and "Shannon-Fano" result in an equivalent code and thus also to the same average code word length.
- Shannon-Fano, on the other hand, never delivers a more effective code than Huffman.