Difference between revisions of "Aufgaben:Exercise 1.4: Maximum Likelihood Decision"
From LNTwww
| (4 intermediate revisions by one other user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
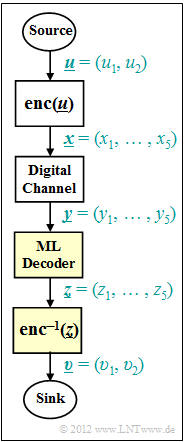
| − | [[File: | + | [[File:EN_KC_A_1_4_neu.png|right|frame|Maximum likelihood decoding model]] |
| − | We consider the digital transmission system according to the graph. Considered are: | + | We consider the digital transmission system according to the graph. Considered are: |
| − | *a systematic $(5, 2)$ block code $\mathcal{C}$ with the code words | + | *a systematic $(5, 2)$ block code $\mathcal{C}$ with the code words |
:$$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm};$$ | :$$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm};$$ | ||
| − | *a digital (binary) channel model that | + | *a digital (binary) channel model that changes the vector $\underline{x} \in {\rm GF} (2^{5})$ over into the vector $\underline{y} \in {\rm GF} (2^{5})$, |
| − | *a [[Channel_Coding/Channel_Models_and_Decision_Structures#Maximum_likelihood_decision_at_the_BSC_channel|Maximum | + | *a [[Channel_Coding/Channel_Models_and_Decision_Structures#Maximum_likelihood_decision_at_the_BSC_channel|Maximum likelihood decoder]] (short: ML decoder) with the decision rule |
:$$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$ | :$$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$ | ||
| − | Here, $d_{\rm H} (\underline{y}, \ \underline{x_{i}})$ the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|Hamming distance]] between the received word $\underline{y}$ and the (possibly) sent | + | Here, $d_{\rm H} (\underline{y}, \ \underline{x_{i}})$ is the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|Hamming distance]] between the received word $\underline{y}$ and the (possibly) sent code word $\underline{x_{i}}$. |
| − | + | Note: This exercise belongs to the chapter [[Channel_Coding/Channel_Models_and_Decision_Structures|"Channel Models and Decision Structures"]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| Line 29: | Line 25: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Let $\underline{y} = (1, 0, 0, 1)$. Which decisions satisfy the maximum likelihood criterion? | + | {Let $\underline{y} = (1, 0, 0, 0, 1)$. Which decisions satisfy the maximum likelihood criterion? |
|type="[]"} | |type="[]"} | ||
| − | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0)$, | + | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, |
- $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | - $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | ||
+ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | + $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| − | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1)$. | + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. |
| − | {Let $\underline{y} = (0, 0, 0, 1, 0)$. Which decisions satisfy the maximum likelihood criterion? | + | {Let $\underline{y} = (0, 0, 0, 1, 0)$. Which decisions satisfy the maximum likelihood criterion? |
|type="[]"} | |type="[]"} | ||
| − | + $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0)$, | + | + $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, |
+ $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | + $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | ||
- $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | - $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| − | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1)$. | + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. |
| − | {What decision does the | + | {What decision does the maximum likelihood decoder make for $\underline{y} = (1, 0, 1, 1, 1)$ when it is told that the last two symbols are uncertain? |
|type="[]"} | |type="[]"} | ||
| − | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0)$, | + | - $\underline{z} = \underline{x}_{0} = (0, 0, 0, 0, 0)$, |
- $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | - $\underline{z} = \underline{x}_{1} = (0, 1, 0, 1, 0)$, | ||
+ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | + $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$, | ||
| − | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1)$. | + | - $\underline{z} = \underline{x}_{3} = (1, 1, 1, 1, 1)$. |
| Line 63: | Line 59: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Correct <u>answer 3</u>: | + | '''(1)''' Correct <u>answer 3</u> ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$: |
| − | *The Hamming distances between the specific received word $\underline{y} = (1, 0, 0, 1)$ and the four possible | + | *The Hamming distances between the specific received word $\underline{y} = (1, 0, 0, 0, 1)$ and the four possible code words $\underline{x}_{i}$ are as follows: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$ | ||
*A decision is made for the sequence with the smallest Hamming distance $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$. | *A decision is made for the sequence with the smallest Hamming distance $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$. | ||
| Line 70: | Line 66: | ||
| − | '''(2)''' For $\underline{y} = (0, 0, 0, 1, 0)$ the <u>answers 1 and 2</u> are correct, as the following calculation shows: | + | '''(2)''' For $\underline{y} = (0, 0, 0, 1, 0)$ the <u>answers 1 and 2</u> are correct, as the following calculation shows: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$ | ||
| − | '''(3)''' Correct <u>answer 3</u>: | + | '''(3)''' Correct <u>answer 3</u> ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$: |
| − | *According to the Hamming distance, a decision in favor of $x_{2}$ would be just as possible as for $x_{3}$ if the vector $\underline{y} = (1, 0, 1, 1, 1)$ is received: | + | *According to the Hamming distance, a decision in favor of $x_{2}$ would be just as possible as for $x_{3}$ if the vector $\underline{y} = (1, 0, 1, 1, 1)$ is received: |
:$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$ | :$$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$ | ||
| − | *But the received vector $\underline{y}$ is different from $x_{2}$ with respect to the fourth bit and from $x_{3}$ in the second bit. | + | *But the received vector $\underline{y}$ is different from $x_{2}$ with respect to the fourth bit and from $x_{3}$ in the second bit. |
| − | * Since the fourth bit is more uncertain than the second, it will choose $x_{2}$ . | + | * Since the fourth bit is more uncertain than the second, it will choose $x_{2}$ . |
| − | '''(4)''' Since this is a systematic code, the decision for $\underline{z} = (1, 0, 1, 0, 1)$ is equivalent to the decision | + | '''(4)''' Since this is a systematic code, the decision for $\underline{z} = (1, 0, 1, 0, 1)$ is equivalent to the decision |
:$$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$ | :$$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$ | ||
| − | *It is not certain that $\underline{u} = (1, 0)$ was actually sent. | + | *It is not certain that $\underline{u} = (1, 0)$ was actually sent. |
| − | *But the probability is highest for this given the received vector $\underline{y} = (1, 0, 1, 1)$. | + | *But the probability is highest for this given the received vector $\underline{y} = (1, 0, 1, 1, 1)$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 17:54, 1 November 2022
We consider the digital transmission system according to the graph. Considered are:
- a systematic $(5, 2)$ block code $\mathcal{C}$ with the code words
- $$\underline{x}_{0} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 0, 0, 0, 0) \hspace{0.05cm},$$ $$\underline{x}_{1} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0, 1, 0, 1, 0) \hspace{0.05cm},$$ $$\underline{x}_{2} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 0, 1, 0, 1) \hspace{0.05cm},$$ $$\underline{x}_{3} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (1, 1, 1, 1, 1) \hspace{0.05cm};$$
- a digital (binary) channel model that changes the vector $\underline{x} \in {\rm GF} (2^{5})$ over into the vector $\underline{y} \in {\rm GF} (2^{5})$,
- a Maximum likelihood decoder (short: ML decoder) with the decision rule
- $$\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i}).$$
Here, $d_{\rm H} (\underline{y}, \ \underline{x_{i}})$ is the Hamming distance between the received word $\underline{y}$ and the (possibly) sent code word $\underline{x_{i}}$.
Note: This exercise belongs to the chapter "Channel Models and Decision Structures".
Questions
Solution
(1) Correct answer 3 ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$:
- The Hamming distances between the specific received word $\underline{y} = (1, 0, 0, 0, 1)$ and the four possible code words $\underline{x}_{i}$ are as follows:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 2\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 3\hspace{0.05cm}.$$
- A decision is made for the sequence with the smallest Hamming distance $d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1$.
(2) For $\underline{y} = (0, 0, 0, 1, 0)$ the answers 1 and 2 are correct, as the following calculation shows:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 4\hspace{0.05cm}.$$
(3) Correct answer 3 ⇒ $\underline{z} = \underline{x}_{2} = (1, 0, 1, 0, 1)$:
- According to the Hamming distance, a decision in favor of $x_{2}$ would be just as possible as for $x_{3}$ if the vector $\underline{y} = (1, 0, 1, 1, 1)$ is received:
- $$d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_0) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_1) = 4\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_2) = 1\hspace{0.05cm}, \hspace{0.3cm} d_{\rm H}(\underline{y}, \hspace{0.05cm}\underline{x}_3) = 1\hspace{0.05cm}.$$
- But the received vector $\underline{y}$ is different from $x_{2}$ with respect to the fourth bit and from $x_{3}$ in the second bit.
- Since the fourth bit is more uncertain than the second, it will choose $x_{2}$ .
(4) Since this is a systematic code, the decision for $\underline{z} = (1, 0, 1, 0, 1)$ is equivalent to the decision
- $$v_{1} \ \underline{ = 1}, \ v_{2} \ \underline{= 0}.$$
- It is not certain that $\underline{u} = (1, 0)$ was actually sent.
- But the probability is highest for this given the received vector $\underline{y} = (1, 0, 1, 1, 1)$.