Difference between revisions of "Aufgaben:Exercise 1.5: HDB3 Coding"
m (Text replacement - "[[Beispiele_von_Nachrichtensystemen" to "[[Examples_of_Communication_Systems") |
|||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Examples_of_Communication_Systems/ISDN_Primary_Multiplex_Connection |
}} | }} | ||
| − | [[File: | + | [[File:EN_Bei_A_1_5.png|right|frame|Signals with HDB3 coding]] |
| − | + | The ISDN primary rate interface $\rm (PRI)$ is based on the $\rm PCM\ system \ 30/32$ and offers | |
| + | *$30$ full-duplex basic channels, | ||
| − | + | *plus a signaling channel | |
| − | |||
| − | |||
| − | + | *and a synchronization channel. | |
| − | * | ||
| − | |||
| − | + | Each of these channels, which are transmitted in time division multiplex, has a data rate of $64 \ \rm kbit/s$. A frame consists of one byte $\rm (8$ bits$)$ of all $32$ channels. The duration of such a frame $($German: "Rahmen"$)$ is denoted by $T_{\rm R}$, while $T_{\rm B}$ indicates the bit duration. | |
| + | On both the $\rm S_{\rm 2M}$ and $\rm U_{\rm K2}$ interfaces of the ISDN system under consideration, the '''HDB3 code''' is used, which is derived from the AMI code. This is a pseudo-ternary code $($symbol set size $M = 3$, symbol duration $T = T_{\rm B})$, that differs from the AMI code in that long zero sequences are avoided by deliberately violating the AMI coding rule. The following applies: | ||
| + | If four consecutive "'''0'''" symbols occur in the AMI-encoded signal $a(t)$, these are replaced by four other ternary symbols: | ||
| + | *If an even number of "+'''1'''" occurred before this four-symbol block the signal $a(t)$ and the last pulse is positive, "'''0 0 0 0'''" is replaced by "– '''0 0''' –". If the last pulse is negative, "'''0 0 0 0'''" is replaced by "+ '''0 0''' +". | ||
| + | *On the other hand, if there is an odd number of "ones" before this "'''0 0 0 0'''" block, "'''0 0 0''' +" $($if last pulse positive$)$ or "'''0 0 0''' –" $($if last pulse negative$)$ are selected. | ||
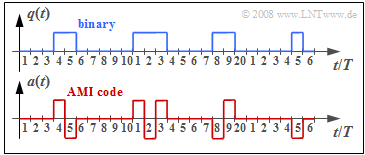
| + | The graph above shows the binary signal $q(t)$ and the signal $a(t)$ after AMI coding. The HDB3 signal is denoted by $c(t)$. | ||
| − | |||
| − | * | + | |
| − | * | + | |
| + | Notes: | ||
| + | |||
| + | *The exercise belongs to the chapter [[Examples_of_Communication_Systems/ISDN_Primary_Multiplex_Connection|"ISDN Primary Multiplex Connection"]] . | ||
| + | *Information about the pseudo-ternary codes can be found in the section [[Digital_Signal_Transmission/Symbolwise_Coding_with_Pseudo-Ternary_Codes|"Symbolwise Coding with Pseudo-Ternary Codes"]] of "Digital Signal Transmission". | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the total data rate of the ISDN rate interface? |
|type="{}"} | |type="{}"} | ||
$R_{\rm B} \ = \ $ { 2.048 3% } $\ \rm Mbit/s$ | $R_{\rm B} \ = \ $ { 2.048 3% } $\ \rm Mbit/s$ | ||
| − | { | + | {What is the bit duration $T_{\rm B}$ and frame duration $T_{\rm R}$? |
|type="{}"} | |type="{}"} | ||
$T_{\rm B} \ = \ $ { 0.488 3% } $\ \rm µ s$ | $T_{\rm B} \ = \ $ { 0.488 3% } $\ \rm µ s$ | ||
$T_{\rm R} \ = \ $ { 125 3% } $\ \rm µ s$ | $T_{\rm R} \ = \ $ { 125 3% } $\ \rm µ s$ | ||
| − | { | + | {How is the zero block between bit '''6''' and bit '''10''' encoded?<br>Possible input values are $0$, $+1$ and $–1$. |
|type="{}"} | |type="{}"} | ||
$c_{6} \ = \ $ { 0 3% } | $c_{6} \ = \ $ { 0 3% } | ||
| Line 53: | Line 58: | ||
$c_{10} \ = \ $ { 0 3% } | $c_{10} \ = \ $ { 0 3% } | ||
| − | { | + | {How is the zero block between bit '''14''' and bit '''17''' encoded? |
|type="{}"} | |type="{}"} | ||
$c_{14} \ = \ $ { 0 3% } | $c_{14} \ = \ $ { 0 3% } | ||
| Line 60: | Line 65: | ||
$c_{17} \ = \ $ { 1 3% } | $c_{17} \ = \ $ { 1 3% } | ||
| − | { | + | {How is the zero block between bit '''20''' and bit '''24''' encoded? |
|type="{}"} | |type="{}"} | ||
$c_{20} \ = \ $ { -1.03--0.97 } | $c_{20} \ = \ $ { -1.03--0.97 } | ||
| Line 70: | Line 75: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The total data rate of the $32$ channels at $64 \ \rm kbit/s$ each results in |
:$$R_{\rm B} \underline{ = 2.048 \ \rm Mbit/s}.$$ | :$$R_{\rm B} \underline{ = 2.048 \ \rm Mbit/s}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The bit duration is $T_{\rm B} = 1/R_{\rm B} \underline{ = 0.488 \ \rm µ s}$. |
| − | * | + | *One byte (8 bits) of each channel is transmitted per frame. It follows that: |
:$$T_{\rm R} = 32 \cdot 8 \cdot T_{\rm B} \hspace{0.15cm}\underline{= 125 \,{\rm µ s}}\hspace{0.05cm}.$$ | :$$T_{\rm R} = 32 \cdot 8 \cdot T_{\rm B} \hspace{0.15cm}\underline{= 125 \,{\rm µ s}}\hspace{0.05cm}.$$ | ||
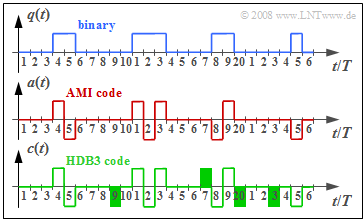
| − | '''(3)''' | + | '''(3)''' By time $t = 6T$, a "+'''1'''" has occurred exactly once in the AMI-encoded signal $a(t)$. |
| − | [[File: | + | [[File:EN_Bei_A_1_5e.png|right|frame|Relationship between AMI code and HDB3 code]] |
| − | * | + | *Because of $a_{5} = –1$, in the HDB3 code "'''0 0 0 0'''" is replaced by (see diagram) |
:$$\underline{c_{6} = 0, \hspace{0.2cm}c_{7} = 0, \hspace{0.2cm}c_{8} = 0, \hspace{0.2cm}c_{9} = -1} \hspace{0.05cm}.$$ | :$$\underline{c_{6} = 0, \hspace{0.2cm}c_{7} = 0, \hspace{0.2cm}c_{8} = 0, \hspace{0.2cm}c_{9} = -1} \hspace{0.05cm}.$$ | ||
| − | * | + | |
| + | * In contrast, $\underline{c_{10} = a_{10} = 0}$ is not changed bythe HDB3 coding. | ||
| − | '''(4)''' | + | '''(4)''' Up to and including $a_{13}$, there are three times a "+1" ⇒ odd number. Because of $a_{12} = +1$, this zero block is replaced as follows: |
:$$ \underline{c_{14} = 0, \hspace{0.2cm}c_{15} = 0, \hspace{0.2cm}c_{16} = 0, \hspace{0.2cm}c_{17} = +1} \hspace{0.05cm}.$$ | :$$ \underline{c_{14} = 0, \hspace{0.2cm}c_{15} = 0, \hspace{0.2cm}c_{16} = 0, \hspace{0.2cm}c_{17} = +1} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' In the AMI-encoded signal, "+1" occurs exactly four times up to and including $a_{19}$ ⇒ even number. |
| − | * | + | *Because of $a_{19} = +1$, the substitution according to rule 2 in the information section is: |
:$$\underline{c_{20} = -1, \hspace{0.2cm}c_{21} = 0, \hspace{0.2cm}c_{22} = 0, \hspace{0.2cm}c_{23} = -1} \hspace{0.05cm}.$$ | :$$\underline{c_{20} = -1, \hspace{0.2cm}c_{21} = 0, \hspace{0.2cm}c_{22} = 0, \hspace{0.2cm}c_{23} = -1} \hspace{0.05cm}.$$ | ||
| − | * | + | *The zero symbol $a_{24}$ remains unchanged: $\underline{c_{24} = 0}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 104: | Line 110: | ||
| − | [[Category: | + | [[Category:Examples of Communication Systems: Exercises|^1.3 ISDN Primary Multiplex Line^]] |
| − | ^]] | ||
Latest revision as of 12:03, 10 November 2022
The ISDN primary rate interface $\rm (PRI)$ is based on the $\rm PCM\ system \ 30/32$ and offers
- $30$ full-duplex basic channels,
- plus a signaling channel
- and a synchronization channel.
Each of these channels, which are transmitted in time division multiplex, has a data rate of $64 \ \rm kbit/s$. A frame consists of one byte $\rm (8$ bits$)$ of all $32$ channels. The duration of such a frame $($German: "Rahmen"$)$ is denoted by $T_{\rm R}$, while $T_{\rm B}$ indicates the bit duration.
On both the $\rm S_{\rm 2M}$ and $\rm U_{\rm K2}$ interfaces of the ISDN system under consideration, the HDB3 code is used, which is derived from the AMI code. This is a pseudo-ternary code $($symbol set size $M = 3$, symbol duration $T = T_{\rm B})$, that differs from the AMI code in that long zero sequences are avoided by deliberately violating the AMI coding rule. The following applies:
If four consecutive "0" symbols occur in the AMI-encoded signal $a(t)$, these are replaced by four other ternary symbols:
- If an even number of "+1" occurred before this four-symbol block the signal $a(t)$ and the last pulse is positive, "0 0 0 0" is replaced by "– 0 0 –". If the last pulse is negative, "0 0 0 0" is replaced by "+ 0 0 +".
- On the other hand, if there is an odd number of "ones" before this "0 0 0 0" block, "0 0 0 +" $($if last pulse positive$)$ or "0 0 0 –" $($if last pulse negative$)$ are selected.
The graph above shows the binary signal $q(t)$ and the signal $a(t)$ after AMI coding. The HDB3 signal is denoted by $c(t)$.
Notes:
- The exercise belongs to the chapter "ISDN Primary Multiplex Connection" .
- Information about the pseudo-ternary codes can be found in the section "Symbolwise Coding with Pseudo-Ternary Codes" of "Digital Signal Transmission".
Questions
Solution
(1) The total data rate of the $32$ channels at $64 \ \rm kbit/s$ each results in
- $$R_{\rm B} \underline{ = 2.048 \ \rm Mbit/s}.$$
(2) The bit duration is $T_{\rm B} = 1/R_{\rm B} \underline{ = 0.488 \ \rm µ s}$.
- One byte (8 bits) of each channel is transmitted per frame. It follows that:
- $$T_{\rm R} = 32 \cdot 8 \cdot T_{\rm B} \hspace{0.15cm}\underline{= 125 \,{\rm µ s}}\hspace{0.05cm}.$$
(3) By time $t = 6T$, a "+1" has occurred exactly once in the AMI-encoded signal $a(t)$.
- Because of $a_{5} = –1$, in the HDB3 code "0 0 0 0" is replaced by (see diagram)
- $$\underline{c_{6} = 0, \hspace{0.2cm}c_{7} = 0, \hspace{0.2cm}c_{8} = 0, \hspace{0.2cm}c_{9} = -1} \hspace{0.05cm}.$$
- In contrast, $\underline{c_{10} = a_{10} = 0}$ is not changed bythe HDB3 coding.
(4) Up to and including $a_{13}$, there are three times a "+1" ⇒ odd number. Because of $a_{12} = +1$, this zero block is replaced as follows:
- $$ \underline{c_{14} = 0, \hspace{0.2cm}c_{15} = 0, \hspace{0.2cm}c_{16} = 0, \hspace{0.2cm}c_{17} = +1} \hspace{0.05cm}.$$
(5) In the AMI-encoded signal, "+1" occurs exactly four times up to and including $a_{19}$ ⇒ even number.
- Because of $a_{19} = +1$, the substitution according to rule 2 in the information section is:
- $$\underline{c_{20} = -1, \hspace{0.2cm}c_{21} = 0, \hspace{0.2cm}c_{22} = 0, \hspace{0.2cm}c_{23} = -1} \hspace{0.05cm}.$$
- The zero symbol $a_{24}$ remains unchanged: $\underline{c_{24} = 0}$.