Difference between revisions of "Aufgaben:Exercise 3.3Z: Convolution and D-Transformation"
From LNTwww
| (One intermediate revision by the same user not shown) | |||
| Line 4: | Line 4: | ||
In this exercise, we use a simple example to describe | In this exercise, we use a simple example to describe | ||
| − | * the finite <b>impulse response</b> of a filter: | + | * the finite »<b>impulse response</b>« of a filter: |
:$$\underline{g} = \left (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_l, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_m \right ) | :$$\underline{g} = \left (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_l, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_m \right ) | ||
\hspace{0.05cm},\hspace{0.2cm}g_l \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$ | \hspace{0.05cm},\hspace{0.2cm}g_l \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$ | ||
| − | * the <b>input sequence</b> of the filter: | + | |
| + | * the »<b>input sequence</b>« of the filter: | ||
:$$\underline{u} = \left (u_0, u_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, u_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) | :$$\underline{u} = \left (u_0, u_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, u_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) | ||
\hspace{0.05cm},\hspace{0.2cm}u_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$ | \hspace{0.05cm},\hspace{0.2cm}u_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$ | ||
| − | * the <b>output sequence</b> of the filter: | + | * the »<b>output sequence</b>« of the filter: |
:$$\underline{x} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) | :$$\underline{x} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) | ||
\hspace{0.05cm},\hspace{0.2cm}x_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}. $$ | \hspace{0.05cm},\hspace{0.2cm}x_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}. $$ | ||
| − | We have adapted the nomenclature for this (digital) filter description to the book "Introduction to Channel Coding". In other $\rm LNTww$ books often $\underline{x}$ denotes the filter input, $\underline{y}$ the filter output, and the impulse response is called $h$ | + | We have adapted the nomenclature for this $($digital$)$ filter description to the book "Introduction to Channel Coding". In other $\rm LNTww$ books often |
| + | # $\underline{x}$ denotes the filter input, | ||
| + | # $\underline{y}$ the filter output, and | ||
| + | # the impulse response is called $\underline{h}$. | ||
| + | |||
| − | In general, for the output sequence corresponding to the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_time_domain| | + | In general, for the output sequence corresponding to the [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_in_the_time_domain| $\text{convolution}$]] : |
| − | :$$\underline{x} = \underline{u}* \underline{g} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right )\hspace{0.05cm},\hspace{0.1cm} {\rm | + | :$$\underline{x} = \underline{u}* \underline{g} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right )\hspace{0.05cm},\hspace{0.1cm} {\rm with} \hspace{0.2cm} x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l}\hspace{0.05cm}.$$ |
| − | We now represent the time functions $\underline{g}, \ \underline{u}$ and $\underline{x}$ by polynomials in a dummy | + | *We now represent the time functions $\underline{g}, \ \underline{u}$ and $\underline{x}$ by polynomials in a dummy variable $D$ and call these the D–transforms: |
:$$\underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | :$$\underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | ||
{G}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{l = 0}^{m} g_l \cdot D\hspace{0.03cm}^l = g_0 + g_1 \cdot D + g_2 \cdot D^2 + \text{...} + g_m \cdot D\hspace{0.03cm}^m\hspace{0.05cm},$$ | {G}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{l = 0}^{m} g_l \cdot D\hspace{0.03cm}^l = g_0 + g_1 \cdot D + g_2 \cdot D^2 + \text{...} + g_m \cdot D\hspace{0.03cm}^m\hspace{0.05cm},$$ | ||
| Line 27: | Line 32: | ||
{X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \text{...} \hspace{0.05cm}.$$ | {X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \text{...} \hspace{0.05cm}.$$ | ||
| − | Thus the (more complicated) convolution becomes a multiplication: | + | *Thus the $($more complicated$)$ convolution becomes a multiplication: |
:$$\underline{x} = \underline{u}* \underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | :$$\underline{x} = \underline{u}* \underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | ||
{X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$ | {X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$ | ||
| − | Formally, this relationship can be demonstrated as follows: | + | *Formally, this relationship can be demonstrated as follows: |
:$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = \sum_{i = 0}^{\infty} \sum_{l = 0}^{m}\hspace{0.1cm} | :$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = \sum_{i = 0}^{\infty} \sum_{l = 0}^{m}\hspace{0.1cm} | ||
g_l \cdot u_{i-l} \cdot D\hspace{0.03cm}^{i} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot \sum_{j = -l}^{\infty} \hspace{0.1cm} | g_l \cdot u_{i-l} \cdot D\hspace{0.03cm}^{i} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot \sum_{j = -l}^{\infty} \hspace{0.1cm} | ||
| Line 39: | Line 44: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Here it was considered that all $u_j$ for $j < 0$ do not exist and can be set to zero. | + | *Here it was considered that all $u_j$ for $j < 0$ do not exist and can be set to zero. |
| − | Both procedures for computing the initial sequence $\underline{x}$, viz. | + | *Both procedures for computing the initial sequence $\underline{x}$ shall be demonstrated for the digital filter outlined above, viz. |
| − | + | # using the convolution, | |
| − | + | # by means of the D–transformation. | |
| − | |||
| − | |||
| − | |||
| Line 52: | Line 54: | ||
| + | <u>Hints:</u> | ||
| + | * The exercise belongs to the chapter [[Channel_Coding/Algebraic_and_Polynomial_Description| "Algebraic and Polynomial Description"]]. | ||
| + | * Refer in particular to the [[Channel_Coding/Algebraic_and_Polynomial_Description#GF.282.29_description_forms_of_a_digital_filter|"GF(2) Description Forms of a Digital Filter"]] section. | ||
| − | + | * In the solution, consider the following identity for calculations in $\rm GF(2)$: | |
| − | * | ||
| − | |||
| − | |||
:$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...}\hspace{0.1cm}= \frac{1}{1+D} \hspace{0.05cm}.$$ | :$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...}\hspace{0.1cm}= \frac{1}{1+D} \hspace{0.05cm}.$$ | ||
| Line 71: | Line 73: | ||
$g_2 \ = \ ${ 0. } | $g_2 \ = \ ${ 0. } | ||
| − | {The sequence $\underline{u} = (1, \, 0, \, 0, \, 1)$ let be finite. What is the | + | {The sequence $\underline{u} = (1, \, 0, \, 0, \, 1)$ let be finite. What is the output sequence? |
|type="()"} | |type="()"} | ||
- $\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. | - $\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. | ||
| Line 78: | Line 80: | ||
- $\underline{x} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ "sequence of ones". | - $\underline{x} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ "sequence of ones". | ||
| − | {The sequence $\underline{u} = (1, \, 1, \, 1)$ let be finite. What is the | + | {The sequence $\underline{u} = (1, \, 1, \, 1)$ let be finite. What is the output sequence? |
|type="()"} | |type="()"} | ||
- $\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. | - $\underline{x} = (1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. | ||
| Line 95: | Line 97: | ||
|type="()"} | |type="()"} | ||
- $\underline{u} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ "sequence of ones" | - $\underline{u} = (1, \, 1, \, 1, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ "sequence of ones" | ||
| − | + $\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \,\text{...}\hspace{0.05cm})$ ⇒ alternating sequence, starting with $1$. | + | + $\underline{u} = (1, \, 0, \, 1, \, 0, \, 1, \, 0, \,\text{...}\hspace{0.05cm})$ ⇒ alternating sequence, starting with "$1$". |
| − | - $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ alternating sequence, starting with $0$. | + | - $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...}\hspace{0.05cm})$ ⇒ alternating sequence, starting with "$0$". |
</quiz> | </quiz> | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The only two filter coefficients different from $0$ are $g_0 \ \underline{= 1}$ and $g_1 \ \underline{= 1}$. | + | '''(1)''' The only two filter coefficients different from $0$ are $g_0 \ \underline{= 1}$ and $g_1 \ \underline{= 1}$. |
| − | *From this follows $g_2 \ \underline{= 0}$ and for the | + | *From this follows $g_2 \ \underline{= 0}$ and for the D–transform of the impulse response: |
:$$\underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 1) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | :$$\underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 1) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | ||
{G}(D) = 1+ D \hspace{0.05cm}.$$ | {G}(D) = 1+ D \hspace{0.05cm}.$$ | ||
| Line 108: | Line 110: | ||
| − | '''(2)''' The impulse response of the considered filter is $\underline{g} = (1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. | + | '''(2)''' The impulse response of the considered filter is $\underline{g} = (1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$. |
| − | *For the | + | *For the output sequence, therefore, we obtain the convolution product |
:$$\underline{x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u}* \underline{g} = | :$$\underline{x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u}* \underline{g} = | ||
(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) * | (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) * | ||
| Line 115: | Line 117: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The same result is obtained using the | + | *The same result is obtained using the D–transforms $U(D) = 1 + D^3$ and $G(D) = 1 + D$: |
:$${X}(D) = U(D) \cdot G(D) = ( 1+D^3) \cdot (1+D) = 1 +D + D^3 +D^4 | :$${X}(D) = U(D) \cdot G(D) = ( 1+D^3) \cdot (1+D) = 1 +D + D^3 +D^4 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The | + | *The inverse transformation leads again to the result $\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$ ⇒ <u>Proposed solution 3</u>. |
| − | '''(3)''' Here we immediately use the path over the | + | '''(3)''' Here we immediately use the path over the D–transforms: |
:$${X}(D) = ( 1+D+D^2) \cdot (1+D) = 1 +D + D +D^2 +D^2 +D^3 = 1+ D^3\hspace{0.3cm} | :$${X}(D) = ( 1+D+D^2) \cdot (1+D) = 1 +D + D +D^2 +D^2 +D^3 = 1+ D^3\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} \underline{x} = | \Rightarrow \hspace{0.3cm} \underline{x} = | ||
| Line 129: | Line 131: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The result corresponds to the <u>proposed solution 2</u>. The following calculation is to illustrate the path in the time domain: | + | *The result corresponds to the <u>proposed solution 2</u>. The following calculation is to illustrate the path in the time domain: |
:$$(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * | :$$(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * | ||
(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$ | (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$ | ||
| Line 137: | Line 139: | ||
(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$ | (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$ | ||
| − | *Since convolution is a linear operation, in the Galois field ${\rm GF}(2)$ results from summation: | + | *Since the convolution is a linear operation, in the Galois field ${\rm GF}(2)$ results from summation: |
:$$(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * | :$$(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * | ||
(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.08cm}=\hspace{0.08cm}(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$ | (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.08cm}=\hspace{0.08cm}(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$ | ||
| − | *If the convolution had been performed not in ${\rm GF}(2)$ but for real numbers, we would have obtained the result $\underline{x} = (1, \, 2, \, 2, \, 1, \, 0, \, 0, \, \text{...})$. | + | *If the convolution had been performed not in ${\rm GF}(2)$ but for real numbers, we would have obtained the result $\underline{x} = (1, \, 2, \, 2, \, 1, \, 0, \, 0, \, \text{...})$. |
| − | '''(4)''' The sample solution to the subtask '''(3)''' already suggests that the <u>proposed solution 1</u> is correct here. | + | '''(4)''' The sample solution to the subtask '''(3)''' already suggests that the <u>proposed solution 1</u> is correct here. |
| − | *The way over the | + | *The way over the D–transforms confirms this result: |
:$$\underline{u} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | :$$\underline{u} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} | ||
{U}(D)= 1+ D + D^2+ D^3 + \text{...}\hspace{0.15cm}.$$ | {U}(D)= 1+ D + D^2+ D^3 + \text{...}\hspace{0.15cm}.$$ | ||
| − | *Using the equation valid for calculations in ${\rm GF}(2)$ | + | *Using the equation valid for calculations in ${\rm GF}(2)$ |
:$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...} \hspace{0.1cm}= \frac{1}{1+D}$$ | :$$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...} \hspace{0.1cm}= \frac{1}{1+D}$$ | ||
| Line 160: | Line 162: | ||
| − | '''(5)''' The path over the | + | '''(5)''' The path over the D–transforms leads to <u>solution 2</u>. |
| − | *For this alternating sequence $\underline{u}$, starting with 1, one obtains: | + | *For this alternating sequence $\underline{u}$, starting with $1$, one obtains: |
:$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot (1+D) + D^2 \cdot (1+D) + D^4 \cdot (1+D) + \text{...} = 1 + D + D^2 + D^3 + D^4 + D^5 +\hspace{0.05cm} ... | :$${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot (1+D) + D^2 \cdot (1+D) + D^4 \cdot (1+D) + \text{...} = 1 + D + D^2 + D^3 + D^4 + D^5 +\hspace{0.05cm} ... | ||
\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| Line 167: | Line 169: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *This result can also be read by direct application of the convolution as in subtask (2). | + | *This result can also be read by direct application of the convolution as in subtask '''(2)'''. |
| − | *With $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...})$ you get $\underline{x} = (0, \, 1, \, 1, \, 1, \, 1, \, 1, \,\text{...})$. | + | |
| − | *This differs from the "sequence of ones" only in the first bit. It is then $x_1 = 0$ instead of $x_1 = 1$. | + | *With $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...})$ you get $\underline{x} = (0, \, 1, \, 1, \, 1, \, 1, \, 1, \,\text{...})$. |
| + | |||
| + | *This differs from the "sequence of ones" only in the first bit. It is then $x_1 = 0$ instead of $x_1 = 1$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Channel Coding: Exercises|^3.2 Polynomial Description^]] | [[Category:Channel Coding: Exercises|^3.2 Polynomial Description^]] | ||
Latest revision as of 17:47, 10 November 2022
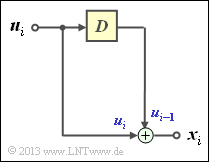
In this exercise, we use a simple example to describe
- the finite »impulse response« of a filter:
- $$\underline{g} = \left (g_0, g_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_l, \hspace{0.05cm}\text{...}\hspace{0.1cm}, g_m \right ) \hspace{0.05cm},\hspace{0.2cm}g_l \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$
- the »input sequence« of the filter:
- $$\underline{u} = \left (u_0, u_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, u_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) \hspace{0.05cm},\hspace{0.2cm}u_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}, $$
- the »output sequence« of the filter:
- $$\underline{x} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right ) \hspace{0.05cm},\hspace{0.2cm}x_i \in {\rm GF(2) } = \{ 0, 1 \}\hspace{0.05cm}. $$
We have adapted the nomenclature for this $($digital$)$ filter description to the book "Introduction to Channel Coding". In other $\rm LNTww$ books often
- $\underline{x}$ denotes the filter input,
- $\underline{y}$ the filter output, and
- the impulse response is called $\underline{h}$.
In general, for the output sequence corresponding to the $\text{convolution}$ :
- $$\underline{x} = \underline{u}* \underline{g} = \left (x_0, x_1, \hspace{0.05cm}\text{...}\hspace{0.1cm}, x_i, \hspace{0.05cm}\text{...}\hspace{0.1cm} \right )\hspace{0.05cm},\hspace{0.1cm} {\rm with} \hspace{0.2cm} x_i = \sum_{l = 0}^{m} g_l \cdot u_{i-l}\hspace{0.05cm}.$$
- We now represent the time functions $\underline{g}, \ \underline{u}$ and $\underline{x}$ by polynomials in a dummy variable $D$ and call these the D–transforms:
- $$\underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {G}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{l = 0}^{m} g_l \cdot D\hspace{0.03cm}^l = g_0 + g_1 \cdot D + g_2 \cdot D^2 + \text{...} + g_m \cdot D\hspace{0.03cm}^m\hspace{0.05cm},$$
- $$\underline{u} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} u_i \cdot D\hspace{0.03cm}^i = u_0 + u_1 \cdot D + u_2 \cdot D^2 + \text{...} \hspace{0.05cm},$$
- $$\underline{x} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = x_0 + x_1 \cdot D + x_2 \cdot D^2 + \text{...} \hspace{0.05cm}.$$
- Thus the $($more complicated$)$ convolution becomes a multiplication:
- $$\underline{x} = \underline{u}* \underline{g} \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$
- Formally, this relationship can be demonstrated as follows:
- $${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{i = 0}^{\infty} x_i \cdot D\hspace{0.03cm}^i = \sum_{i = 0}^{\infty} \sum_{l = 0}^{m}\hspace{0.1cm} g_l \cdot u_{i-l} \cdot D\hspace{0.03cm}^{i} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot \sum_{j = -l}^{\infty} \hspace{0.1cm} u_{j} \cdot D\hspace{0.03cm}^{j+l} = \sum_{l = 0}^{m} \hspace{0.1cm} g_l \cdot D\hspace{0.03cm}^l \hspace{0.1cm} \cdot \hspace{0.1cm} \sum_{j = 0}^{\infty} \hspace{0.1cm} u_{j} \cdot D\hspace{0.03cm}^{j}$$
- $$\Rightarrow \hspace{0.3cm}{X}(D) = U(D) \cdot G(D) \hspace{0.05cm}.$$
- Here it was considered that all $u_j$ for $j < 0$ do not exist and can be set to zero.
- Both procedures for computing the initial sequence $\underline{x}$ shall be demonstrated for the digital filter outlined above, viz.
- using the convolution,
- by means of the D–transformation.
Hints:
- The exercise belongs to the chapter "Algebraic and Polynomial Description".
- Refer in particular to the "GF(2) Description Forms of a Digital Filter" section.
- In the solution, consider the following identity for calculations in $\rm GF(2)$:
- $$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...}\hspace{0.1cm}= \frac{1}{1+D} \hspace{0.05cm}.$$
Questions
Solution
(1) The only two filter coefficients different from $0$ are $g_0 \ \underline{= 1}$ and $g_1 \ \underline{= 1}$.
- From this follows $g_2 \ \underline{= 0}$ and for the D–transform of the impulse response:
- $$\underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 1) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {G}(D) = 1+ D \hspace{0.05cm}.$$
(2) The impulse response of the considered filter is $\underline{g} = (1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$.
- For the output sequence, therefore, we obtain the convolution product
- $$\underline{x} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u}* \underline{g} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) =(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} ...\hspace{0.05cm}) \hspace{0.05cm}.$$
- The same result is obtained using the D–transforms $U(D) = 1 + D^3$ and $G(D) = 1 + D$:
- $${X}(D) = U(D) \cdot G(D) = ( 1+D^3) \cdot (1+D) = 1 +D + D^3 +D^4 \hspace{0.05cm}.$$
- The inverse transformation leads again to the result $\underline{x} = (1, \, 1, \, 0, \, 1, \, 1, \, 0, \, 0, \, \text{...}\hspace{0.05cm})$ ⇒ Proposed solution 3.
(3) Here we immediately use the path over the D–transforms:
- $${X}(D) = ( 1+D+D^2) \cdot (1+D) = 1 +D + D +D^2 +D^2 +D^3 = 1+ D^3\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$
- The result corresponds to the proposed solution 2. The following calculation is to illustrate the path in the time domain:
- $$(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$
- $$(0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ...\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm},$$
- $$(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm})\hspace{-0.15cm} \ = \ \hspace{-0.15cm}(0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$
- Since the convolution is a linear operation, in the Galois field ${\rm GF}(2)$ results from summation:
- $$(1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) * (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm})\hspace{0.08cm}=\hspace{0.08cm}(1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1 \hspace{0.05cm}\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0,\hspace{0.05cm} \text{...}\hspace{0.05cm}) \hspace{0.05cm}.$$
- If the convolution had been performed not in ${\rm GF}(2)$ but for real numbers, we would have obtained the result $\underline{x} = (1, \, 2, \, 2, \, 1, \, 0, \, 0, \, \text{...})$.
(4) The sample solution to the subtask (3) already suggests that the proposed solution 1 is correct here.
- The way over the D–transforms confirms this result:
- $$\underline{u} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.05cm}) \hspace{0.25cm} \circ\!\!-\!\!\!-^{\hspace{-0.25cm}D}\!\!\!-\!\!\bullet\hspace{0.25cm} {U}(D)= 1+ D + D^2+ D^3 + \text{...}\hspace{0.15cm}.$$
- Using the equation valid for calculations in ${\rm GF}(2)$
- $$1 + D + D^2 + D^3 + \hspace{0.05cm}\text{...} \hspace{0.1cm}= \frac{1}{1+D}$$
- one further obtains:
- $${X}(D) = U(D) \cdot G(D) = \frac{1}{1+D} \cdot (1+D) = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm}\text{...} \hspace{0.05cm}) \hspace{0.05cm}.$$
(5) The path over the D–transforms leads to solution 2.
- For this alternating sequence $\underline{u}$, starting with $1$, one obtains:
- $${X}(D) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 \cdot (1+D) + D^2 \cdot (1+D) + D^4 \cdot (1+D) + \text{...} = 1 + D + D^2 + D^3 + D^4 + D^5 +\hspace{0.05cm} ... \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x} = (1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} \text{...} \hspace{0.05cm}) \hspace{0.05cm}.$$
- This result can also be read by direct application of the convolution as in subtask (2).
- With $\underline{u} = (0, \, 1, \, 0, \, 1, \, 0, \, 1, \, \text{...})$ you get $\underline{x} = (0, \, 1, \, 1, \, 1, \, 1, \, 1, \,\text{...})$.
- This differs from the "sequence of ones" only in the first bit. It is then $x_1 = 0$ instead of $x_1 = 1$.